题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：
输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：
输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：
输入：nums1 = [2], nums2 = []
输出：2.00000


提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000

  • -10 <= nums1[i], nums2[i] <= 10


    进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

解题思路

1、使用归并

使用归并的方式，合并两个有序数组，得到一个大的有序数组。大的有序数组的中间位置的元素，即为中位数。

时间复杂度是 O(m+n)，空间复杂度是 O(m+n)

2、双指针法

不需要合并两个有序数组，只要找到中位数的位置即可。由于两个数组的长度已知，因此中位数对应的两个数组的下标之和也是已知的。维护两个指针，初始时分别指向两个数组的下标 0 的位置，每次将指向较小值的指针后移一位（如果一个指针已经到达数组末尾，则只需要移动另一个数组的指针），直到到达中位数的位置。

虽然可以将空间复杂度降到 O(1)，但是时间复杂度仍是 O(m+n)

3、二分查找

如何把时间复杂度降低到 O(log(m+n)) 呢？如果对时间复杂度的要求有 log，通常都需要用到二分查找，这道题也可以通过二分查找实现。

根据中位数的定义，当 m+n 是奇数时，中位数是两个有序数组中的第 (m+n)/2 个元素，当 m+n 是偶数时，中位数是两个有序数组中的第 (m+n)/2 个元素和第 (m+n)/2+1 个元素的平均值。因此，这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为 (m+n)/2 或 (m+n)/2+1。

由于两个数组长度之和 m+n 的奇偶不确定，因此需要分情况来讨论。

对于奇数的情况，直接找到最中间的数即可，偶数的话需要求最中间两个数的平均值。

假设两个有序数组分别是 A 和 B。要找到第 k 个元素，我们可以比较 A[k/2-1] 和 B[k/2-1]，其中 / 表示整数除法。由于 A[k/2-1] 和 B[k/2-1] 的前面分别有 A[0..k/2-2] 和 B[0..k/2-2]，即 k/2-1 个元素，对于 A[k/2-1] 和 B[k/2-1] 中的较小值，最多只会有 (k/2-1)+(k/2-1)≤k−2 个元素比它小，那么它就不能是第 k 小的数了。

因此我们可以归纳出三种情况：

  • 如果 A[k/2-1] < B[k/2-1]，则比 A[k/2-1] 小的数最多只有 A 的前 k/2-1 个数和 B 的前 k/2-1 个数，即比 A[k/2-1] 小的数最多只有 k-2 个，因此 A[k/2−1] 不可能是第 k 个数，A[0] 到 A[k/2−1] 也都不可能是第 k 个数，可以全部排除。
  • 如果 A[k/2−1]>B[k/2−1]，则可以排除 B[0] 到 B[k/2−1]。
  • 如果 A[k/2−1]=B[k/2−1]，则可以归入第一种情况处理。

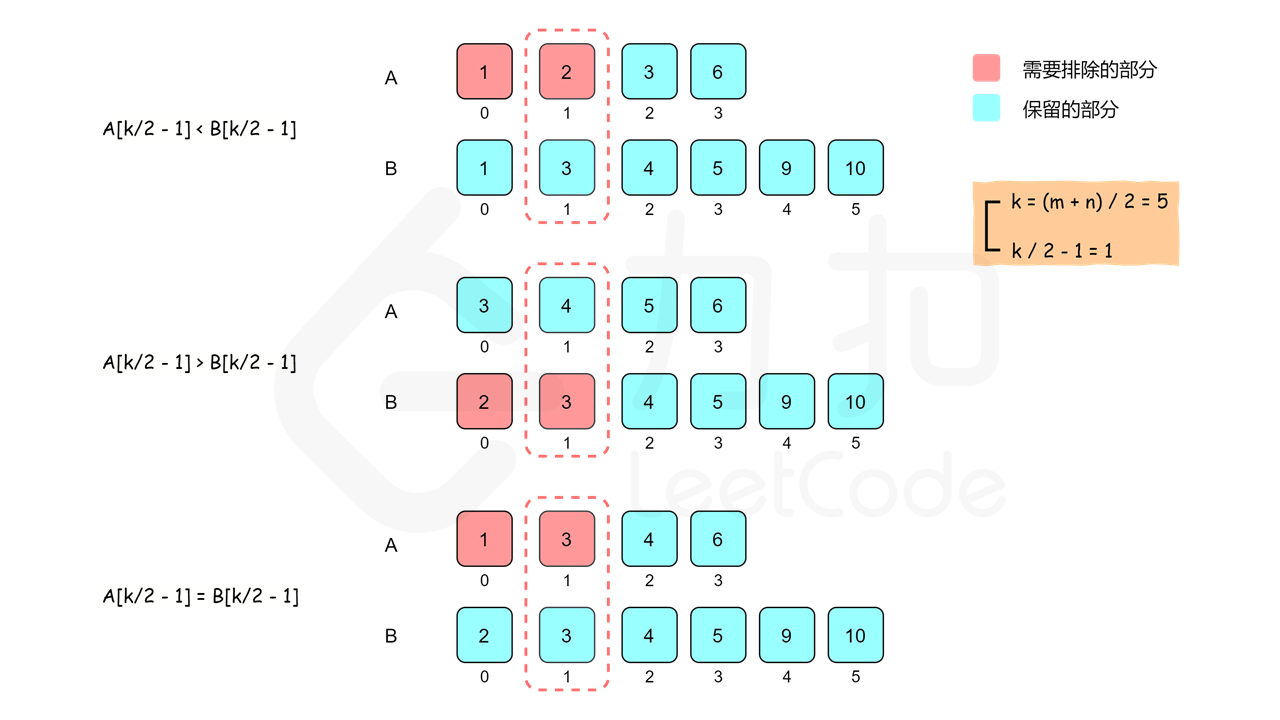
4. 寻找两个正序数组的中位数（困难） - 图1

可以看到，比较 A[k/2−1] 和 B[k/2−1] 之后，可以排除 k/2 个不可能是第 k 小的数，查找范围缩小了一半。同时，我们将在排除后的新数组上继续进行二分查找，并且根据我们排除数的个数，减少 kk 的值，这是因为我们排除的数都不大于第 kk 小的数。

有以下三种情况需要特殊处理：

  • 如果 A[k/2−1] 或者 B[k/2−1] 越界，那么我们可以选取对应数组中的最后一个元素。在这种情况下，我们必须根据排除数的个数减少 kk 的值，而不能直接将 kk 减去 k/2。
  • 如果一个数组为空，说明该数组中的所有元素都被排除，我们可以直接返回另一个数组中第 k 小的元素。
  • 如果 k=1，我们只要返回两个数组首元素的最小值即可。

答案

1、使用归并

  1. class Solution {
  2.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  3.         // 结果
  4.         double result = 0;
  6.         // 两个 int 数组的长度
  7.         int length1 = nums1.length;
  8.         int length2 = nums2.length;
  10.         // 两个 int 数组的长度之和为奇数或偶数 奇数为1 偶数为0
  11.         int isOdd = (length1 + length2) % 2;
  12.         // 中位数下标 如果长度之和为奇数，则中位数下标就为 flag ，如果为偶数，中位数为 flag 和 flag - 1 之和 / 2
  13.         int flag = (length1 + length2) / 2;
  15.         // 缓存数组
  16.         int[] temp = new int[nums1.length + nums2.length];
  18.         // 遍历下标
  19.         int i = 0, j = 0, k = 0;
  20.         while (i < length1 || j < length2) {
  21. //            System.out.println("i: " + i);
  22. //            System.out.println("j: " + j);
  23. //            System.out.println("k: " + k);
  24. //            System.out.println();
  26.             if (i < length1 && j < length2) {
  27.                 // nums1 和 nums2 都未处理完
  29.                 // 判断 A 和 B 哪个小
  30.                 if (nums1[i] <= nums2[j]) {
  31.                     // A 小等于 B
  33.                     temp[k] = nums1[i];
  34.                     i++;
  35.                 } else {
  36.                     // B 比 A 小
  38.                     temp[k] = nums2[j];
  39.                     j++;
  40.                 }
  42.                 // 判断是否为中位数
  43.                 if (isOdd == 1) {
  44.                     // 奇数个
  45.                     if (k == flag) {
  46.                         // 是中位数
  47.                         result = temp[k];
  48.                         break;
  49.                     }
  50.                 } else {
  51.                     // 偶数个
  52.                     if (k == flag) {
  53.                         // 是中位数
  54.                         result = (temp[k] + temp[k - 1]) / 2.0;
  55.                         break;
  56.                     }
  57.                 }
  59.                 k++;
  60.                 continue;
  61.             }
  63.             if (i < length1) {
  64.                 // nums1 尚未处理完 , nums2 已处理完
  66.                 // 插入temp
  67.                 temp[k] = nums1[i];
  68.                 i++;
  70.                 // 判断是否为中位数
  71.                 if (isOdd == 1) {
  72.                     // 奇数个
  73.                     if (k == flag) {
  74.                         // 是中位数
  75.                         result = temp[k];
  76.                         break;
  77.                     }
  78.                 } else {
  79.                     // 偶数个
  80.                     if (k == flag) {
  81.                         // 是中位数
  82.                         result = (temp[k] + temp[k - 1]) / 2.0;
  83.                         break;
  84.                     }
  85.                 }
  87.                 k++;
  88.                 continue;
  89.             }
  91.             if (j < length2) {
  92.                 // nums2 尚未处理完 , nums1 已处理完
  94.                 // 插入temp
  95.                 temp[k] = nums2[j];
  96.                 j++;
  98.                 // 判断是否为中位数
  99.                 if (isOdd == 1) {
  100.                     // 奇数个
  101.                     if (k == flag) {
  102.                         // 是中位数
  103.                         result = temp[k];
  104.                         break;
  105.                     }
  106.                 } else {
  107.                     // 偶数个
  108.                     if (k == flag) {
  109.                         // 是中位数
  110.                         result = (temp[k] + temp[k - 1]) / 2.0;
  111.                         break;
  112.                     }
  113.                 }
  115.                 k++;
  116.                 continue;
  117.             }
  118.         }
  120. //        System.out.println("-----------------------------");
  121. //        System.out.println("length1: " + length1);
  122. //        System.out.println("length1: " + length2);
  123. //        System.out.println("isOdd: " + isOdd);
  124. //        System.out.println("flag: " + flag);
  125. //        System.out.println(Arrays.toString(temp));
  127.         return result;
  128.     }
  129. }

2、双指针法

…

3、二分查找

  1. class Solution {
  2.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  3.         // 两个数组的元素个数
  4.         int length1 = nums1.length;
  5.         int length2 = nums2.length;
  7.         // 第 k 小值
  8.         int k = (length1 + length2) / 2;
  10.         if ((length1 + length2) % 2 == 1) {
  11.             // 奇数个
  12.             return find(nums1, nums2, k);
  13.         } else {
  14.             // 偶数个
  15.             return (find(nums1, nums2, k) + find(nums1, nums2, k + 1)) / 2.0;
  16.         }
  18.     }
  20.     // 求两个排序好的数组中，第 k 小的数
  21.     public double find(int[] nums1, int[] nums2, int k) {
  22.         // nums1 与 nums2 的游标
  23.         int i = 0, j = 0;
  25.         // 两个数组的元素个数
  26.         int length1 = nums1.length;
  27.         int length2 = nums2.length;
  29.         while (true) {
  30.             // 边界
  31.             if (i >= length1) {
  32.                 return nums2[j + k - 1];
  33.             }
  34.             if (j >= length2) {
  35.                 return nums1[i + k - 1];
  36.             }
  37.             if (k == 1) {
  38.                 return Math.min(nums1[i], nums2[j]);
  39.             }
  41.             // 正常情况
  42.             int halfK = k / 2;
  43.             int newIndexI = Math.min(i + halfK, length1) - 1;
  44.             int newIndexJ = Math.min(j + halfK, length2) - 1;
  45.             if (nums1[newIndexI] <= nums2[newIndexJ]) {
  46.                 k = k - (newIndexI - i + 1);
  47.                 i = newIndexI + 1;
  48.             } else {
  49.                 k = k - (newIndexJ - j + 1);
  50.                 j = newIndexJ + 1;
  51.             }
  52.         }
  53.     }
  54. }