题目

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：
P A H N
A P L S I I G
Y I R
之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数：
string convert(string s, int numRows);

示例 1：
输入：s = “PAYPALISHIRING”, numRows = 3
输出：“PAHNAPLSIIGYIR”

示例 2：
输入：s = “PAYPALISHIRING”, numRows = 4
输出：“PINALSIGYAHRPI”
解释：
P I N
A L S I G
Y A H R
P I

示例 3：
输入：s = “A”, numRows = 1
输出：“A”

提示：

• 1 <= s.length <= 1000
• s 由英文字母（小写和大写）、',' 和 '.' 组成
• 1 <= numRows <= 1000

解题思路

1、按行排序

通过从左向右迭代字符串，我们可以轻松地确定字符位于 Z 字形图案中的哪一行。

从左到右迭代 s，将每个字符添加到合适的行。可以使用当前行和当前方向这两个变量对合适的行进行跟踪。
只有当我们向上移动到最上面的行或向下移动到最下面的行时，当前方向才会发生改变。

• 时间复杂度：O(n)，其中 n = len(s)
• 空间复杂度：O(n)

2、按行访问

逐行读取 Z 字形图案的字符。
首先访问 行 0 中的所有字符，接着访问 行 1，然后 行 2，依此类推…

对于所有整数 k，

• 行 0 中的字符位于索引 k (2 · numRows - 2) 处;
• 行numRows−1 中的字符位于索引 k(2⋅numRows−2)+numRows−1 处;
• 内部的 行 i 中的字符位于索引 k(2⋅numRows−2)+i 以及 (k+1)(2⋅numRows−2)−i 处;

虽然执行效率较高，但发现其中规律并总结，编写出优雅的代码其实并不容易，在面试时不太推荐使用这种解法。

答案

1、按行排序

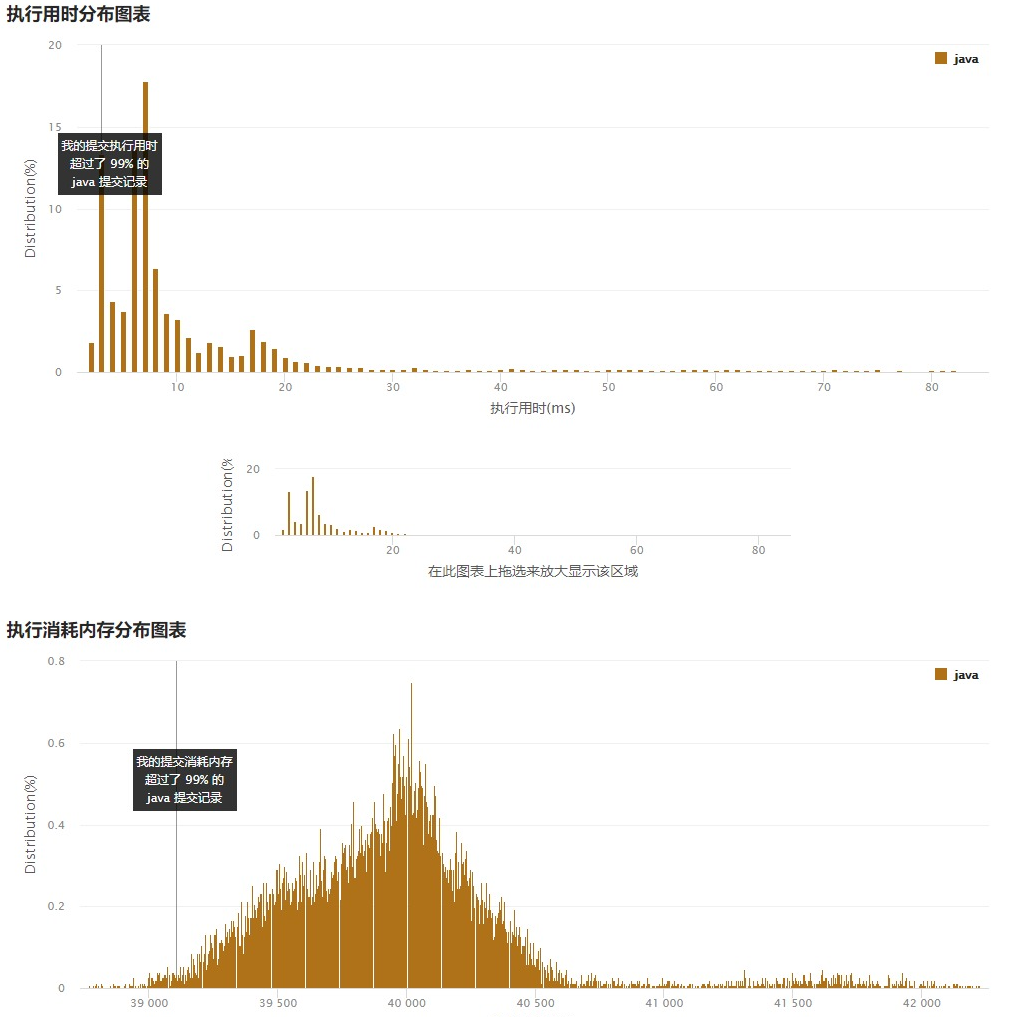
class Solution {
    public String convert(String s, int numRows) {
        // 特殊情况
        if (numRows == 1) {
            return s;
        }
        // 字符串长度
        int len = s.length();
        // 结果
        StringBuffer result = new StringBuffer("");
        // numRows 个 StringBuffer 数组，按照顺序模拟放入，最后拼接到 result
        StringBuffer[] strs = new StringBuffer[numRows];
        for (int i = 0; i < numRows; i++) {
            // 初始化
            strs[i] = new StringBuffer("");
        }
        // 模式：true 为 index 递增 ，false 为 index 递减
        boolean isAdd = true;
        // 计数器
        int index = 0;
        for (int i = 0; i < len; i++) {
            strs[index].append(s.charAt(i));
            if (isAdd) {
                // index 递增
                index++;
            } else {
                // index 递减
                index--;
            }
            if (index == numRows - 1) {
                // 如果相等，说明该切换为递减模式了
                isAdd = false;
            } else if (index == 0) {
                // 如果等于 0，说明下次该切换为递增模式了
                isAdd = true;
            }
        }
        // 拼接结果
        for (int i = 0; i < strs.length; i++) {
            result.append(strs[i]);
        }
        return result.toString();
    }
}

2、按行访问

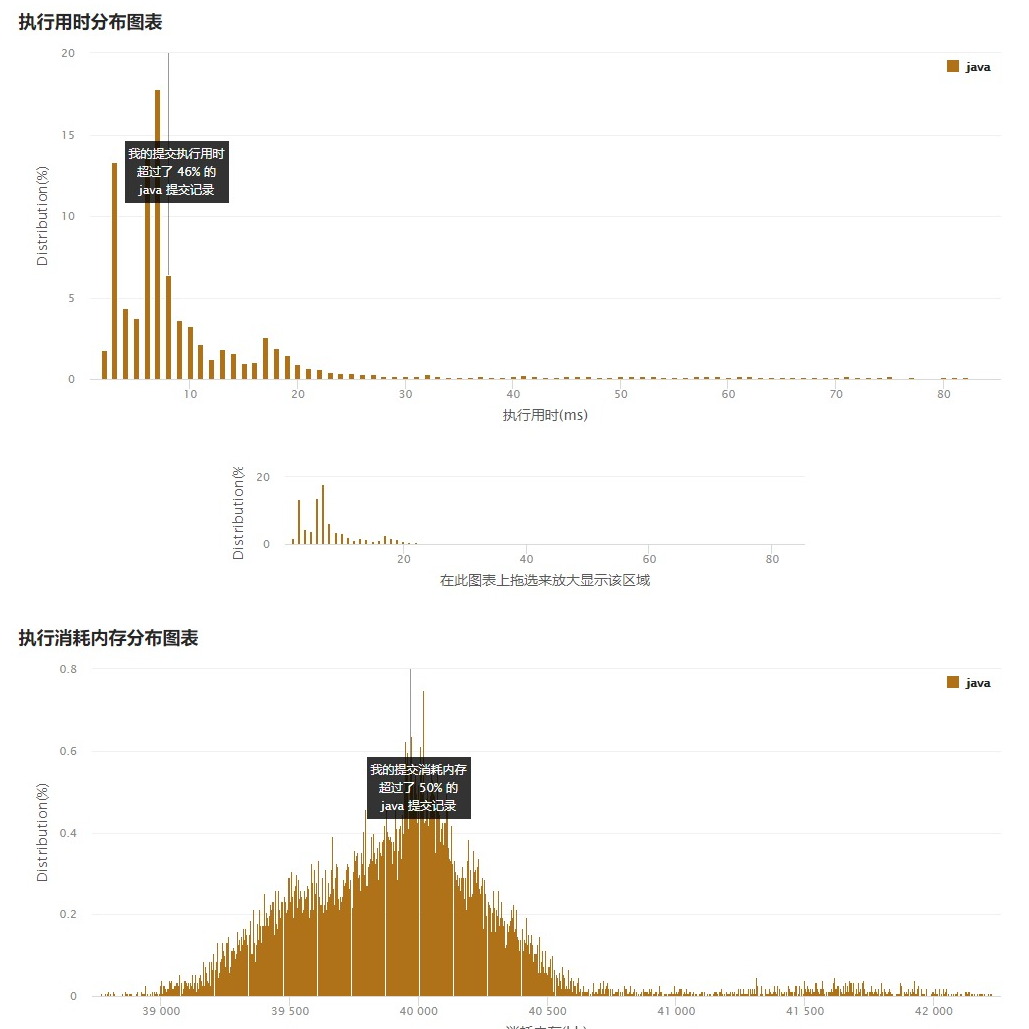
class Solution {
    public String convert(String s, int numRows) {
        // 特殊情况
        if (numRows == 1) return s;
        // 结果
        StringBuilder result = new StringBuilder();
        int n = s.length();
        int cycleLen = 2 * numRows - 2;
        for (int i = 0; i < numRows; i++) {
            for (int j = 0; j + i < n; j += cycleLen) {
                result.append(s.charAt(j + i));
                if (i != 0 && i != numRows - 1 && j + cycleLen - i < n)
                    result.append(s.charAt(j + cycleLen - i));
            }
        }
        return result.toString();
    }
}