前言

Training stuck ≠ Small Gradient

首先纠正一个错误的观念：训练卡主以后（Loss不再降低）并不代表梯度等于零，即并不是走到了critical point（local minimum或者鞍点（saddle point））。即critical point并不是训练过程中遇到的最大难题。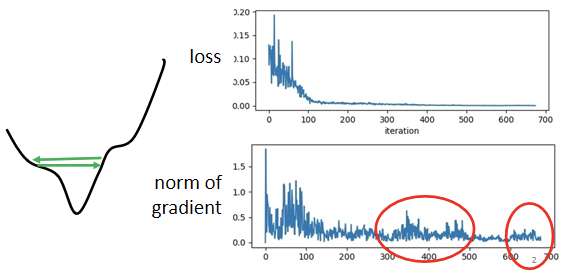

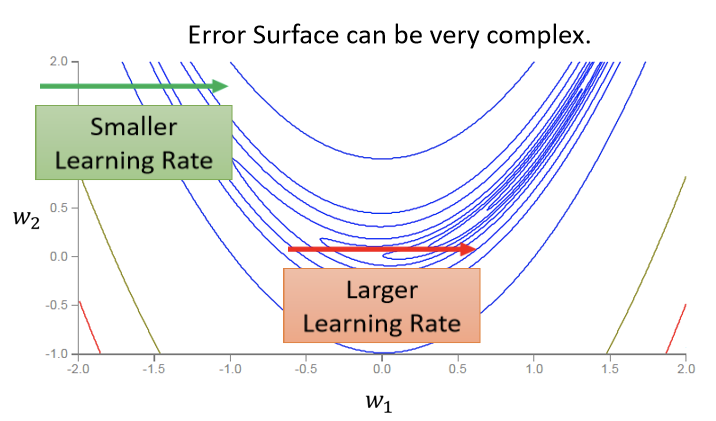
如上图，很大概率上均是训练卡在了山谷两侧频繁震荡，此刻梯度并不一定接近于零，反而有很大可能还很大，而且此刻的Loss也不再下降，其实还有很大的下降空间。这个情况下原本的训练方法（不进行任何改进的梯度下降法）其实已经不够了。

由下实例进行说明：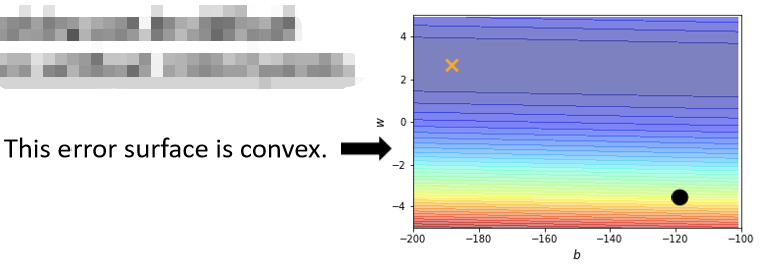

如上图这个模型仅有两个参数，绘出error surface后最低点其实在黄色的X所在的位置。
【注】：error surface是convex的形状(可以理解为凸的或者凹的，convex optimization常翻译为“凸优化”)。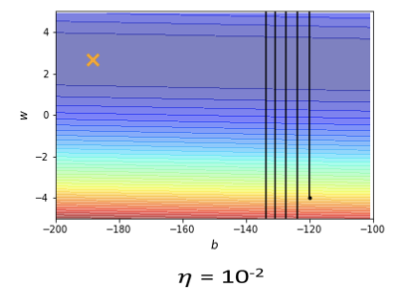

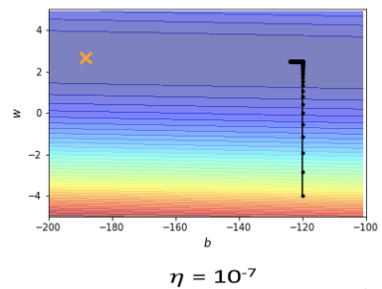
上述两幅图是在不同参数下参数更新的情况。后一张图是不停减少的情况下找到的相对好的情况了。

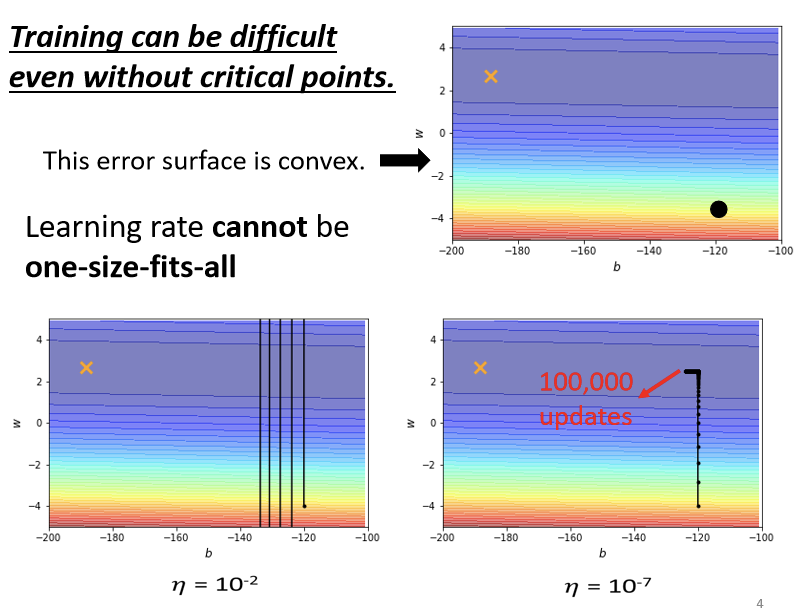
实际上右图在后面粗线的部分已经更新了100，000次参数，可以预计的是即使再怎么修改的值也不能得到根本性的改变，因为在很大的时候如左图，参数更新步幅太大会导致更新曲线一直处于一个幅度很大的震荡情况，理想的情况因该是更新曲线直直下去然后左拐直达X点，可是在调小以后，虽然实现了坡度足够陡峭的地方的参数更新，但是到了蓝色盆地的时候，坡度不够陡峭参数则无法更新到目的地。
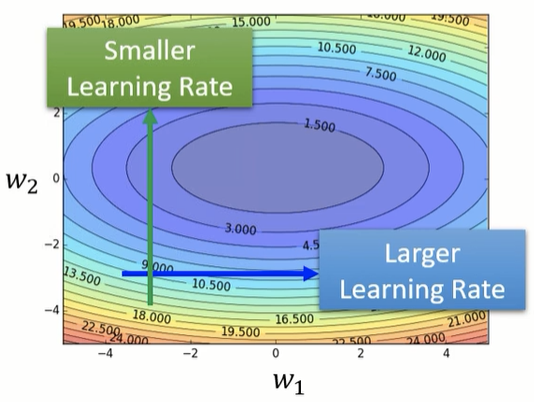
由此可以提出一个想法，即可以随着坡度的陡峭程度实时变换，在梯度大的时候，更新步幅小，梯度小的时候，更新步幅大。

RMS(Root Mean Square)

Different parameters needs different learning rate

原始的梯度下降法公式如下，具体参数表示不再赘述：

其中：

现在将第一小节的想法，即（learning rate）随着梯度的改变的想法加入上式中，令：

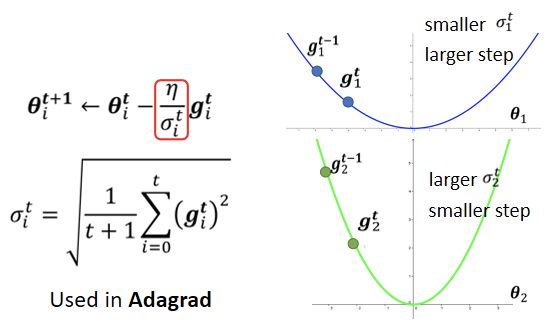
其中这个参数解释如下：（很明显梯度大的时候这个参数也大，的新值会变小）

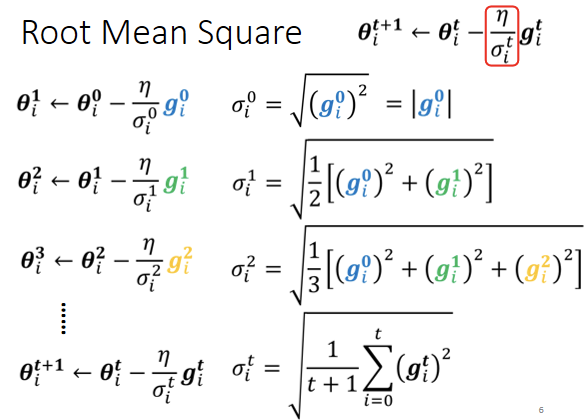
上图中表述了对其中一种表示方法，即计算gradient的root mean square（均方根），新公式表示如下：

其中初始化的时候展示如下：

其他参数大同小异，此处不表。
关于上图error surface除了利用上述方式进行优化外，还有一种方式见Batch Normalization。
具体效果随后展示。

Adagrad（简）

上述RMS计算方法新生成的的值，使用在机器学习Adagrad算法中。

RMSProp

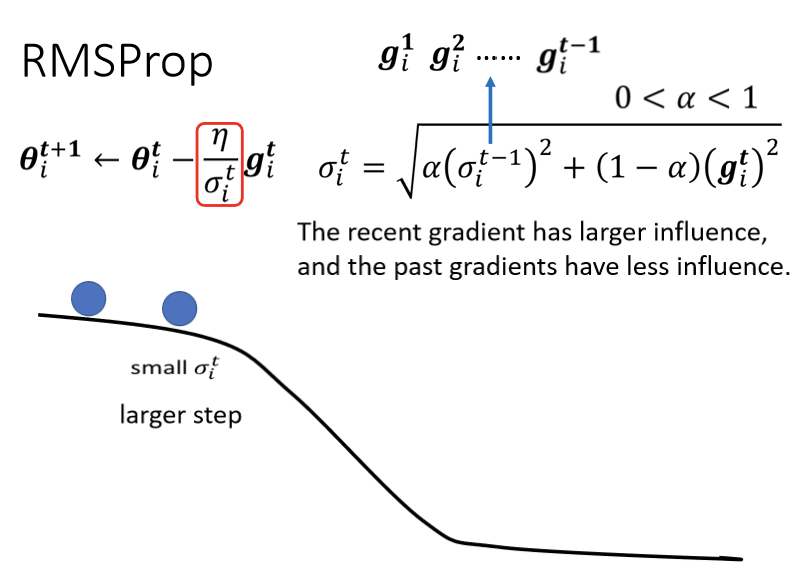
如上图所示需求，想让learning rate也是可以动态调整，RMS Prop应用而生，如下图：

RMS Prop这个方法有点传奇，它传奇的地方在於它找不到论文，非常多年前应该是将近十年前，Hinton在Coursera上，开过deep learning的课程，那个时候他在他的课程裡面，讲了RMS Prop这个方法，然后这个方法没有论文，这是个传奇的方法叫做RMS Prop

RMS Prop方法，它的初始化步骤Root Mean Square，也跟Apagrad的方法是一模一样的。
其中是自己定的，是一个hyperparameter。若想让之前累计的梯度的影响小一点，或者即将遇到较大的坡度的时候，根号下边的（1-α）那一项的梯度会很大，则的值设小一点，这样就会变大，则η会变小，即参数更新步幅会变小。反之则设大一点。如下图：

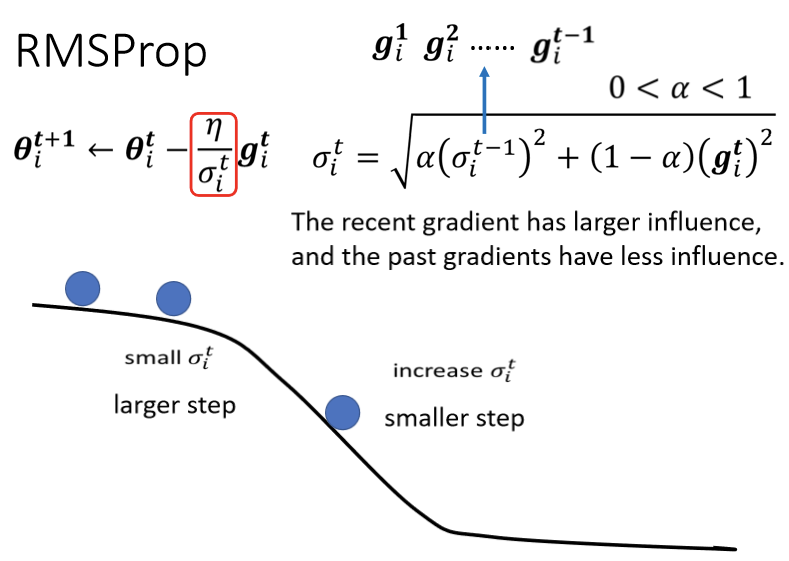
Adam

现在比较常用的Optimization策略即Adam，就是之前讲过的Momentum和这节所述的RMSProp。

Learning Rate Scheduling

回到之前的实验，采用刚才经过改良的算法，即可得下述结果：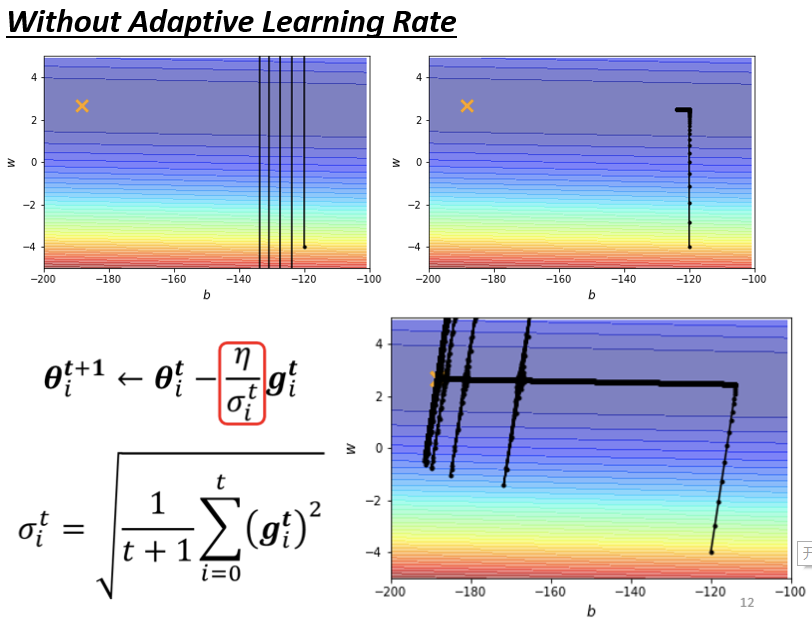

回到之前的实验，η的更新采用RMS方法，新方法最终是可以达到目的的，在使用Adagrad以后，可以再继续走下去，走到非常接近终点的位置。在更新到之前实验卡主的地方的时候，因為存在左右方向上的gradient，虽然很小但是仍然存在，所以learning rate会自动调整，更新步伐就不会始终原地踏步，可以不断的前进。 接下来的问题就是，为什么快走到终点的时候会有突然纵向的位移，实际原因是在做这个σ的时候，是把过去所有的gradient，都拿来作平均：

• 因为在纵轴的方向，初始的时候，gradient很大。
• 在更新了一段路以后，开始左移，即便纵轴方向的gradient算出来都很小，但并不是不存在。累积到一定程度以后，更新的step就会在纵轴开始有大幅度的偏移，而此实验这个方向上是一个峡谷，所以会有一段时间的震荡。
• 震荡以后模型有办法修正回来，因为开始震荡以后，就开始出现gradient比较大的点，在gradient比较大的地方，σ也会慢慢的变大，必然会使参数update的距离慢慢的变小。

上述问题有一个方法可以解决，这个叫做learning rate的scheduling。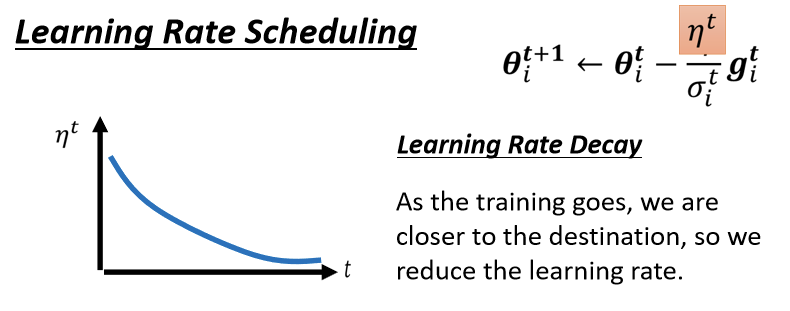

此方法最大的特点即是，不但learning rate随着梯度变化，其本身也会随着时间进行改变。不要把η当一个常数，让它跟时间相关关。最常见的策略叫做Learning Rate Decay__，也就是说，随著时间的不断地进行，随著参数不断的update，η会越来越小。为啥随着时间减少，解释比较玄学，比如远古paper中以前会有一种warm up的方法，没有人会告诉你为什么这么做—！比较靠谱的一种猜测是：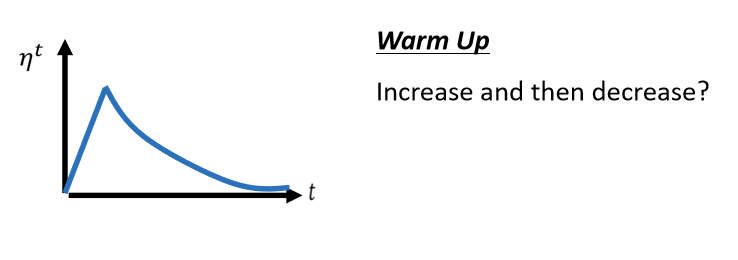

要看得够多笔数据以后，这个统计才精準，所以一开始我们的σ是不精準的，所以我们一开始不要让我们的参数，走离初始的地方太远，先让它在初始的地方呢，做一些像是探索这样，所以一开始learning rate比较小，是让它探索收集一些有关error surface的情报，先收集有关σ的统计数据，等σ统计得比较精準以后，在让learning rate呢慢慢地爬升。所以这是一个解释，為什麼我们需要warm up的可能性，那如果你想要学更多，有关warm up的东西的话，你其实可以看一篇paper，它是Adam的进阶版叫做RAdam，裡面对warm up这件事情，有更多的理解。

回到上述方法，之前的实验在使用了这种方法后，结果集如下图：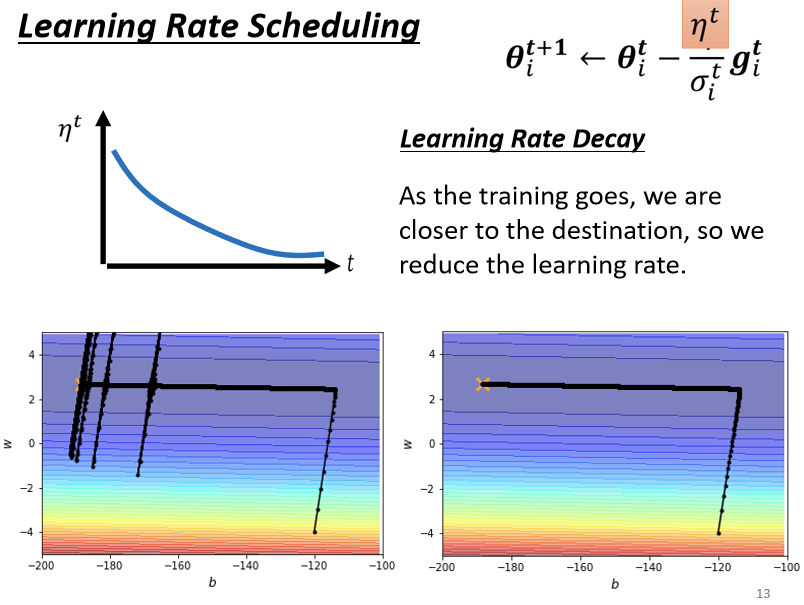

可以看到这次的参数更新非常平滑，而且很好的达到了预期。

Summary

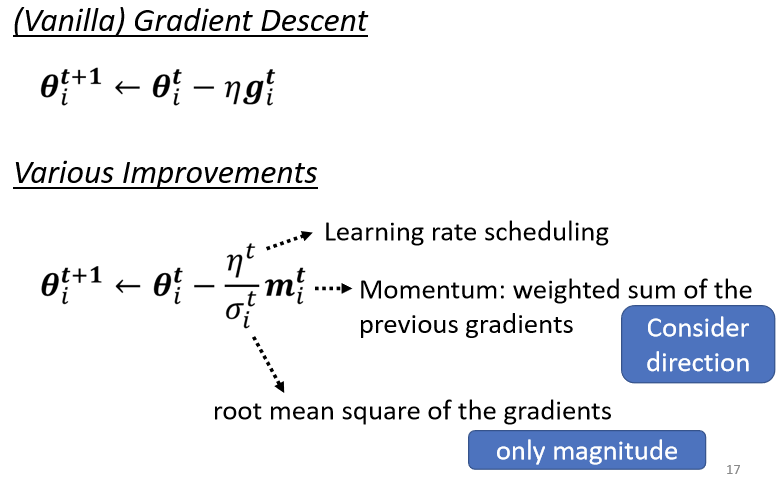
如上图：参数更新的过程揭示了本节的内容，需要注意的是，如图上所述，不仅有数值的大小，还有方向的大小，即它是一个矢量。而是一个标量它仅有大小，目的是为了约束的大小。
TODO:待办Learning rate scheduling具体如何调整并未说明，emmm猜测与更新参数次数有关，待具体练习过后在此处增加心得。