Optimization(When gradient is small)

Critical Point

training fails because

此部分仅讨论Optimization，即如何将梯度下降做的更好，首先了解为什么Optimization会失败。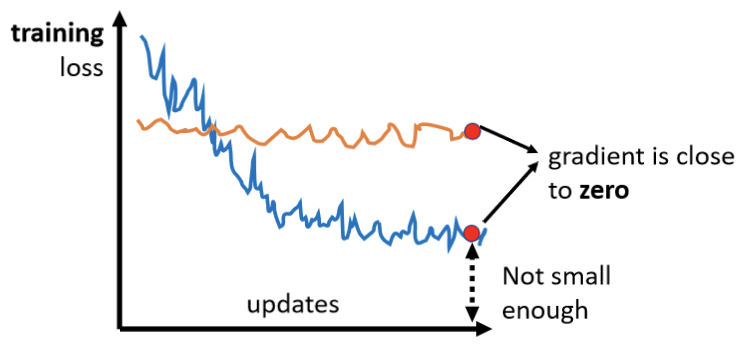

常常在做Optimization的时候，会发现，随著你的参数不断的更新，training的loss不会再下降，但是这个loss并不是较优解，就像之前所描述，将deep的network，跟linear的model，或与shallow network 比较，发现并没有比后述的model的Loss更低，所以Optimization显然是有问题的。 有时候也会出现，一开始你的model就train不起来，一开始你不管怎麼update你的参数，你的loss通通都掉不下去，那这个时候到底发生了什麼事情呢？ 过去常见的一个猜想，是因為我们现在走到了一个地方，这个地方参数对loss的微分為零，当你的参数对loss微分為零的时候，gradient descent就没有办法再update参数了，这个时候training就停下来了，loss当然就不会再下降了。 讲到gradient為零的时候，大家通常脑海中最先浮现的，可能就是local minimum，所以常有人说做deep learning，用gradient descent会卡在local minima，然后gradient descent不工作。

【注】：但是如果有一天要写跟deep learning相关paper的时候，千万不要讲卡在local minima这种事情，别人会觉得你非常没有水准。

如上图，并不是所有的梯度为零的点都是local minimum，也有可能是saddle point（鞍点），可以说卡在critical point的地方。

为什么我们想要知道到底是卡在local minima，还是卡在saddle point呢

• 如果是卡在local minima，那可能就没有路可以走了，因為四周都比较高，你现在所在的位置已经是最低的点，loss最低的点了，往四周走 loss都会比较高，你会不知道怎麼走到其他的地方去。
• 但saddle point就比较没有这个问题，如果你今天是卡在saddle point的话，saddle point旁边还是有路可以走的，还是有路可以让你的loss更低的，你只要逃离saddle point，你就有可能让你的loss更低

所以鉴别critical point到底是local minima还是saddle point，是一个值得去探讨的问题。

那怎麼知道今天一个critical point，到底是属于local minima，还是saddle point呢？

Tayler Series Approximation

如果给定某一组参数，比如说下图蓝色的，在附近的loss function，它写出来就像是这个样子（泰勒展开）：

【注】：H表示为Hessian（海森矩阵），对任一未知数的二次微分。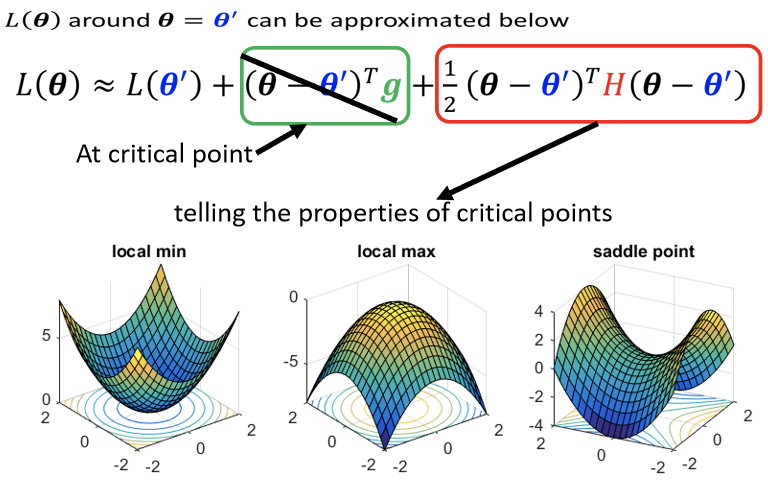

如上图，在critical point的地方g为0（梯度为0），则它可以被近似為加上红色的这一项，则可以根据海森矩阵来判断，在附近的error surface，是一个local minima，亦或是一个local maxima，还是一个saddle point。
接下来便是如何根据Hessian，来判断θ’附近的地貌。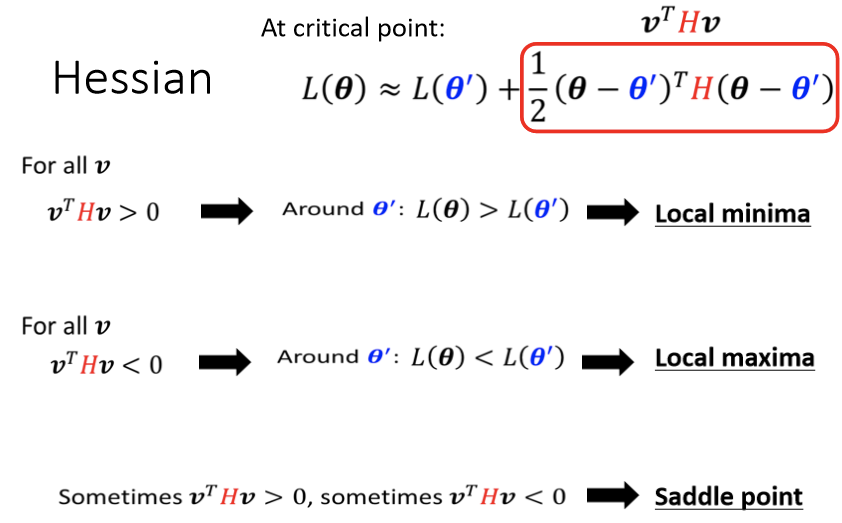

如上图所述：将任意v带入公式实际去求，但是实际情况并不允许。

【结论】：线性代数理论中，对所有的v而言，都大於零，那这种矩阵叫做positive definite （正定矩阵），positive definite的矩阵，它所有的eigen value（特征值）都是正的。

所以如果你今天算出一个hessian，你不需要把它跟所有的v都乘看看，你只要去直接看这个H的eigen value，如果你发现：

• 所有eigen value都是正的，那就代表Critical point就是local minima。
• 对所有的v而言小于零，H便是negative definite，代表所有eigen value都是负的，就保证他是local maxima。
• 如果eigen value有正有负，那就代表是saddle point。

举例说明：

我们现在有一个史上最废的network，它只有一个neuron，而且这个neuron，还没有activation function，所以x乘上以后之后就输出，然后再乘上然后就再输出，就得到最终的数据就是y。总之这个function非常的简单 我们有一个史上最废的training set，我们只有一笔data，这笔data是x，是1的时候，它的level是1 ，所以输入1进去，你希望最终的输出跟1越接近越好 而这个史上最废的training，它的error surface，也是有办法直接画出来的，因為反正只有两个参数 w₁ w₂，连bias都没有，假设没有bias，只有w₁跟w₂两个参数，这个network只有两个参数 w₁跟w₂，那我们可以穷举所有w₁跟w₂的数值，算出所有w₁ w₂数值所代来的loss，然后就画出error surface 长这个样：

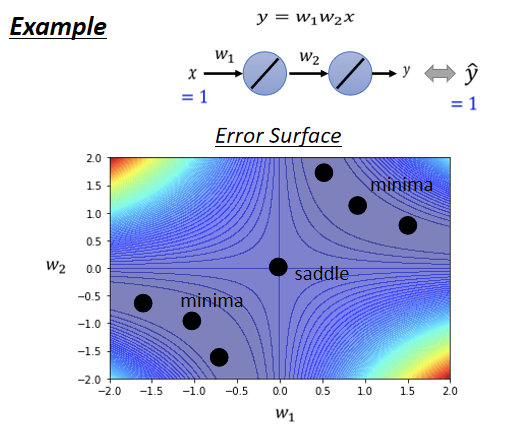
四个角落loss是高的，在这个图上有一些critical point，(0，0)原点的地方是critical point，然后事实上，右上三个黑点也是一排critical point，左下三个点也是一排critical point 如果更进一步要分析，是saddle point，还是local minima，原点这个地方是saddle point，為什麼是saddle point呢？ 往左上方向走 loss会变大，往右下方向走 loss会变大，往左下这个方向走 loss会变小，往右下这个方向走 loss会变小，所以是一个saddle point 而这两群critical point，它们都是local minima，然后在原点的地方，有一个saddle point，这个是我们把error surface，暴力所有的参数，得到的loss function以后，画出error surface，可以得到这样的结论。 现在假设如果不暴力所有可能的loss，如果要直接算说一个点，是local minima，还是saddle point的话 怎麼算呢？

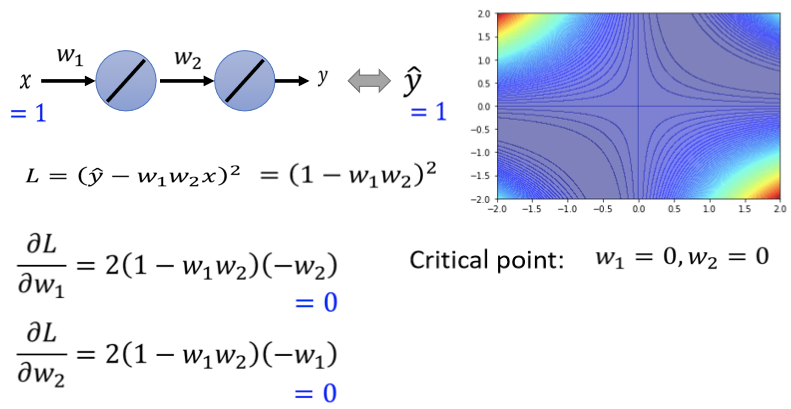
我们可以把loss的function写出来，这个loss的function 这个L是： 它的gradient求出来，w₁对L的微分，w₂对L的微分写出来是这个样子： 上式就是所谓的gradient，什麼时候gradient会零呢，什麼时候会到一个critical point呢? 举例来说 如果w₁=0 w₂=0，就在圆心这个地方，如果w₁代0 w₂代0，w₁对L的微分 w₂对L的微分，算出来就都是零，这个时候我们就知道说，原点就是一个critical point，但它是local maxima，它是local maxima，local minima，还是saddle point呢，那你就要看hessian才能够知道了。

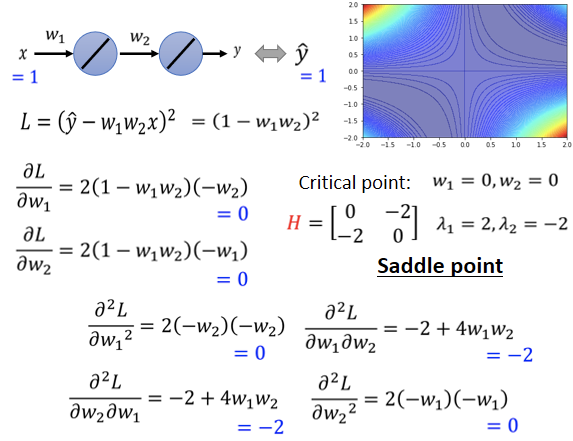
如上图即为海森矩阵，它是local minima，还是saddle point呢，那你就要看这个矩阵的eigen value，算一下发现，这个矩阵有两个eigen value，2跟-2，eigen value有正有负，代表saddle point。

与此同时，在遇到鞍点（saddle point）的时候，海森矩阵还揭示了参数更新的方向，如下图所示：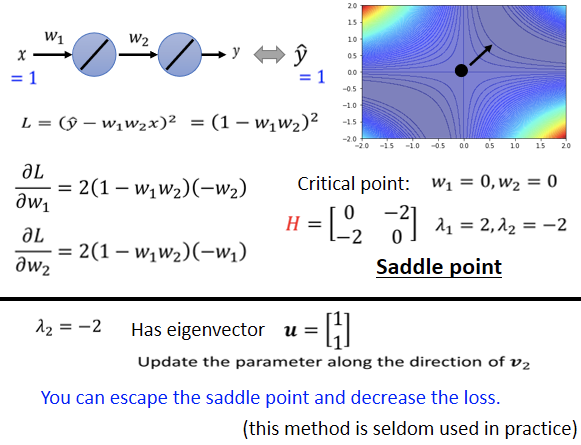

即在特征是为负的特征向量的方向上进行参数更新。

但是在实际的implementation中，你几乎不会真的把Hessian算出来，需要的运算量非常非常的大，更遑论你还要把它的eigen value，跟eigen vector找出来，所以在实际操作中，你几乎没有看到，有人用这一个方法来逃离saddle point。 当然别的更好的逃离saddle point的方法，他们的运算量都比要算这个H，还要小很多，那今天之所以我们把，这个saddle point跟 eigen vector，跟Hessian的eigen vector拿出来讲，是想说，如果是卡在saddle point，也许没有那麼可怕，最糟的状况下你还有这一招，可以告诉你要往哪一个方向走。

「扩展」

这个故事发生在1543年，那一年君士坦丁堡沦陷，君士坦丁堡本来是东罗马帝国的领土，然后被鄂图曼土耳其帝国佔领了，然后东罗马帝国就灭亡了，在鄂图曼土耳其人进攻君士坦丁堡的时候，那时候东罗马帝国的国王，是君士坦丁十一世，他不知道要怎麼对抗土耳其人，有人就献上了一策，找来了一个魔法师叫做狄奥伦娜，这是真实的故事，出自三体的故事，狄奥伦娜是谁呢，他有一个能力跟张飞一样，张飞不是可以万军从中取上将首级如探囊取物吗，狄奥伦娜也是一样，他可以直接取得那个苏丹的头，他可以从万军中取得苏丹的头，大家想说狄奥伦娜怎麼这麼厉害，他真的有这麼强大的魔法吗，所以大家就要狄奥伦娜，先展示一下他的力量，这时候狄奥伦娜就拿出了一个圣杯，大家看到这个圣杯就大吃一惊，為什麼大家看到这个圣杯，要大吃一惊呢，因為这个圣杯，本来是放在圣索菲亚大教堂的地下室，而且它是被放在一个石棺裡面，这个石棺是密封的，没有人可以打开它。但是狄奥伦娜他从裡面取得了圣杯，而且还放了一串葡萄进去，君士坦丁十一世為了要验证，狄奥伦娜是不是真的有这个能力，就带了一堆人真的去撬开了这个石棺，发现圣杯真的被拿走了，裡面真的有一串新鲜的葡萄，就知道狄奥伦娜真的有这个万军从中取上将首级的能力，那為什麼迪奥伦娜可以做到这些事呢，那是因為这个石棺你觉得它是封闭的，是因為你是从三维的空间来看，这个石棺是封闭的，没有任何路可以进去，但是狄奥伦娜可以进入四维的空间，从高维的空间中，这个石棺是有路可以进去的，它并不是封闭的，至於狄奥伦娜有没有成功刺杀苏丹呢，你可以想像一定是没有嘛，所以君坦丁堡才沦陷，那至於為什麼没有，大家请见於三体。

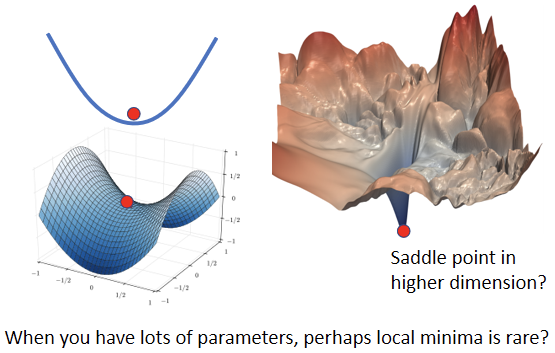
三维的空间来看，是没有路可以走的东西，在高维的空间中是有路可以走的，error surface会不会也一样呢？

我的这边现在有一个local minima，但是会不会这个local minima，只是在二维的空间中，看起来是一个local minima，在更高维的空间中，它看起来就是saddle point，在二维的空间中，我们没有路可以走，那会不会在更高的维度上，因為更高的维度，我们没办法visualize它，我们没办法真的拿出来看，会不会在更高维的空间中，其实有路可以走的，那如果维度越高，是不是可以走的路就越多了呢，所以今天我们在训练一个network的时候，我们的参数往往动輒百万千万以上，所以我们的error surface，其实是在一个非常高的维度中，对不对，我们参数有多少，就代表我们的error surface的维度有多少，参数是一千万就代表error surface的维度是一千万，竟然维度这麼高，会不会其实，根本就有非常多的路可以走呢，那既然有非常多的路可以走，会不会其实local minima，根本就很少呢。 而实际上，如果你自己做一些实验的话，也支持这个假说：

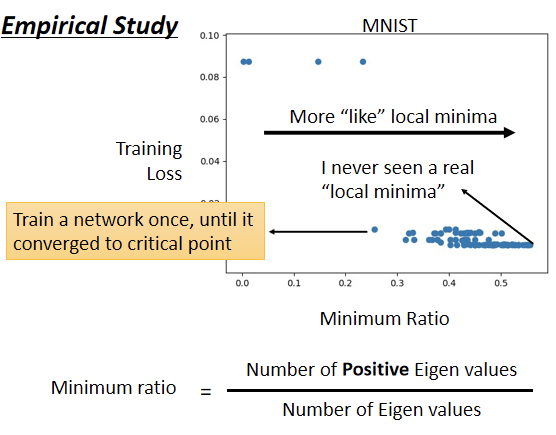
上图是训练某一个network的结果，每一个点代表某个network训练完之后，把它的Hessian拿出来进行计算的结果，所以这边的每一个点，都代表一个network。我们训练某一个network使其gradient很小，卡在critical point，把那组参数拿出来分析，看看它比较像是saddle point，还是比较像是local minima。

• 纵轴代表training的时候的loss，就是我们今天卡住了，那个loss没办法再下降了，那个loss是多少，那很多时候，你的loss在还很高的时候，训练就不动了，就卡在critical point，那很多时候loss可以降得很低，才卡在critical point，这是纵轴的部分。
• 横轴的部分是minimum ratio，minimum ratio是eigen value的数目分之正的eigen value的数目，如果所有的eigen value都是正的，代表我们今天的critical point，是local minima，如果有正有负代表saddle point。在实际情况下上你会发现说，你几乎找不到完全所有eigen value都是正的critical point，你看这边这个例子裡面，这个minimum ratio代表eigen value的数目分之正的eigen value的数目，最大也不过0.5到0.6间而已，代表说只有一半的eigen value是正的，还有一半的eigen value是负的。

所以今天虽然在这个图上，越往右代表我们的critical point越像local minima，但是它们都没有真的，变成local minima，就算是在最极端的状况，我们仍然有一半的case，我们的eigen value是负的，这一半的case eigen value是正的，代表说在所有的维度裡面有一半的路，这一半的路 如果要让loss上升，还有一半的路可以让loss下降。 所以从经验上看起来，其实local minima并没有那麼常见，多数的时候你觉得你训练到一个地方，然后你的参数不再update了，往往是因為你卡在了一个saddle point。