Batch

Small Batch v.s. Large Batch

image.png

现在来比较左右两边两个 Case，假设有20笔训练资料

  • 左边的 Case 是没有用Batch Size，大小设置为和训练资料一样多，这种状况叫Full Batch，即没有用Batch。
  • 右边的 Case 是Batch Size设置为1

这是两个最极端的状况。 先观察左边的Case，因為没有用Batch，所以Model必须把20笔训练资料都看完，才能够计算 Loss，进而计算 Gradient，所以必须要把所有20笔 Examples 都看完以后，参数才能够 Update一次。图左表示把所有资料都看完以后，Update 参数从上边直接移动到下边。 如果 Batch Size 等于1的话，代表只需要拿一笔资料出来算 Loss，就可以 Update 参数。即在每一个 Epoch 裡面，参数会 Update 20次，只不过只看一笔资料，就 Update 一次参数，故算出来的 Loss显然是比较 Noisy 的，所以右图Update的方向是曲折的。

所以如果比较左边跟右边，哪一个比较好？他们又有什麼差别？
image.png

形象地说，左边没有用 Batch 的方式，它蓄力的时间比较长，要把所有的资料都看过一遍，才能够 Update 一次参数。而右边的这个方法，Batch Size 等於1的时候，蓄力的时间比较短，每次看到一笔资料，你就会更新一次你的参数。 所以假设有20笔资料，将所有资料看过一遍后已经更新了20次的参数，但是左边的方法有一个优点，就是它这一步走的是稳的，右边这个方法它的缺点是它每一步走的是不稳的。 左边的方法跟右边的方法，他们各自都有优缺点，左边是蓄力时间长，效果比较好，右边技能冷却时间短，但是它是比较不准的，如果觉得说，左边的方法技能冷却时间长，右边的方法技能冷却时间短，那只是你没有考虑并行运算的问题。 实际上考虑并行运算的话，左边这个并不一定时间比较长。

Larger batch size does not require longer time to compute gradient

先说结论：事实上，比较大的 Batch Size，你要算 Loss，再进而算 Gradient所需要的时间，不一定比小的 Batch Size 要花的时间长。

那以下是做在一个叫做MNIST上面，MNIST (Mixed National Institute of Standards and Technology database)是美国国家标准与技术研究院收集整理的大型手写数字数据库，机器要做的事情，就是给它一张图片，然后判断这张图片，是0到9的哪一个数字，它要做数字的分类，MNIST 相当于是机器学习的helloworld。

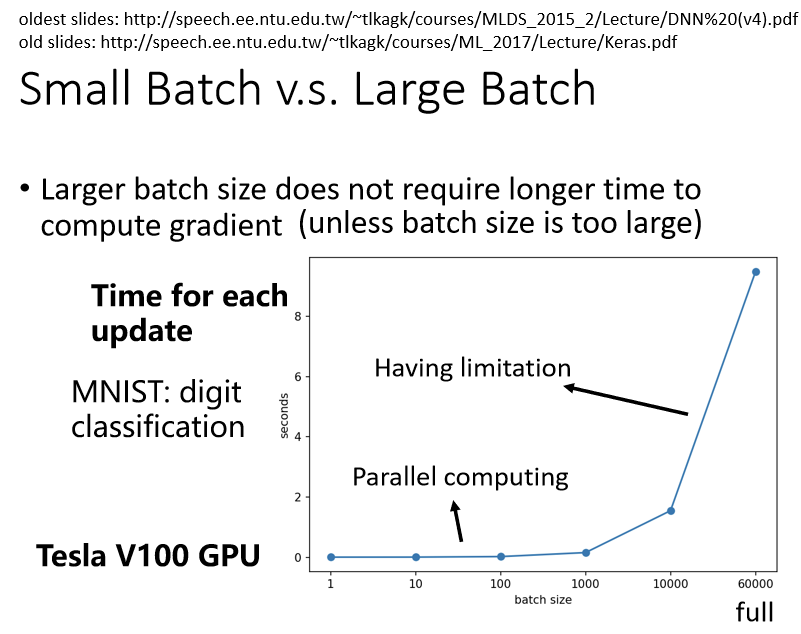
image.png

上图即是一个时间耗费实验，目的是想知道若给机器一个 Batch，它要计算出 Gradient，进而 Update 参数，到底需要花多少的时间。 上边列出了 Batch Size 等於1、等於10、等於100、等於1000所需要耗费的时间。 会发现Batch Size从1到1000，需要耗费的时间几乎是一样的，直觉上认为1000笔资料需要计算 Loss，然后计算 Gradient，花的时间不应该是一笔资料的1000倍吗？但是实际上并不是这样的。 在实际上做运算的时候，可以做并行运算，这1000笔资料是平行处理的，所以1000笔资料所花的时间，并不是一笔资料的1000倍，当然GPU平行运算的能力还是有它的极限，当你的Batch Size 真的非常非常巨大的时候，GPU 在跑完一个 Batch，计算出 Gradient 所花费的时间，还是会随著 Batch Size 的增加，而逐渐增长 所以上图如果Batch Size是从1到1000，所需要的时间几乎是一样的。但是当你的 Batch Size 增加到 10000，乃至增加到60000的时候，就会发现 GPU 要算完一个 Batch，即把这个 Batch 裡面的资料都拿出来算 Loss，再进而算 Gradient，所要耗费的时间，确实有随著 Batch Size 的增加而逐渐增长。

Smaller batch requires longer time for one epoch

image.png

但是因為有平行运算的能力，因此实际上，当你的Batch Size小的时候，你要跑完一个 Epoch，花的时间是比大的Batch Size还要多的。 假设我们的训练资料只有60000笔，那Batch Size设1，则需要60000个 Update才能跑完一个 Epoch，如果Batch Size 等於1000，要60个 Update 才能跑完一个 Epoch，假设今天一个 Batch Size 等於1000，要算Gradient 的时间根本差不多，那60000次 Update，跟60次 Update 比起来，它的时间的差距量就非常可观了，即如上图所示。 如果我们看右边这个图的话，看完一个 Batch，把所有的资料看过一次这件事情，大的 Batch Size 反而是较有效率的，跟直觉正好相反。 在没有考虑平行运算的时候，你觉得大的 Batch 比较慢，但实际上，在有考虑平行运算的时候，一个 Epoch 大的 Batch 花的时间反而是比较少的

image.png

由上述分析可知，大的Batch，Update比较稳定，小的 Batch它的 Gradient 的方向比较 Noisy。那这样看起来，大的 Batch好像应该比较好，小的Batch 应该比较差，因為现在大的 Batch 的劣势已经因為平行运算的时间被拿掉了，它好像只剩下优势。 神奇的地方是Noisy的Gradient，反而可以帮助Training，这个也是跟直觉正好相反。

拿不同的 Batch 来训练模型，可能会得到下图这样的结果，左边是坐在 MNIST上，右边是坐在CIFAR-10（均是影像辨识问题）上。

image.png

  • 横轴代表的是 Batch Size，从左到右越来越大
  • 纵轴代表的是正确率，越上面正确率越高

现在去看 Validation Acc 上的结果，会发现，Batch Size 越大，Validation Acc 上的结果越差，但这个不是 Overfitting，因為如果你看模型的Training 的话，会发现Batch Size越大，Training 的结果也是越差的，而现在使用的是同一个模型，照理说，它们可以表示的 Function就是一模一样的。 但是神奇的事情是，大的 Batch Size，往往在 Training 的时候，会带来比较差的结果。 同样的Model，所以这不是Model Bias的问题，这个是Optimization的问题，当用大的Batch Size的时候，Optimization 可能会有问题，小的 Batch Size，Optimization 的结果反而是比较好的，为什么会这样子呢？

“Noisy” update is better for training

为什么小的 Batch Size，在 Training Set 上会得到比较好的结果，即Noisy 的 Update，Noisy 的 Gradient 会在 Training 的时候，给得到比较好的结果呢？一个可能的解释是这样子的：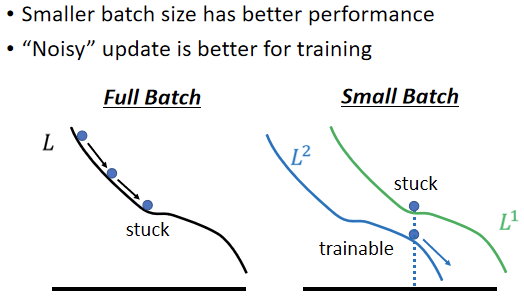
image.png

假设分包策略是Full Batch，那在 Update 参数的时候，就是沿著一个Loss Function 来 Update 参数，假如Update 参数的时候走到一个 Local Minima，或者走到一个 Saddle Point，显然update过程会停下来，如果不特别去检查Hession矩阵的话，用 Gradient Descent 的方法，就没有办法再更新参数了。 但是假如是Small Batch，因为每次是挑一个 Batch 出来，算它的 Loss，所以等於是每次 Update参数的时候，使用的Loss Function都是有差异的，选到第一个 Batch 的时候，是用 L1 来算Gradient，选到第二个 Batch的时候，你是用 L2 来算Gradient，假设用 L1 算 Gradient 的时候，发现Gradient是零，卡住了，但L2的Function跟L1又不一样，L2 就不一定会卡住，所以 L1 卡住了 没关係，换下一个 Batch来，再算 Gradient。 总归还是有办法训练模型，还是有办法让Loss 变小，所以这种Noisy的 Update 的方式，结果反而对 Training其实是有帮助的。

“Noisy” update is better for generalization

另外一个更神奇的事情，其实小的 Batch 对 Testing data 也有帮助。
以下这个实验结果是引用自：

On Large-Batch Training For Deep Learning，Generalization Gap And Sharp Minima https://arxiv。org/abs/1609。04836

【注】：下文中，大的batch是指batch的数量大，即在总数量一定的情况下，batch size越小，batch的规模越大。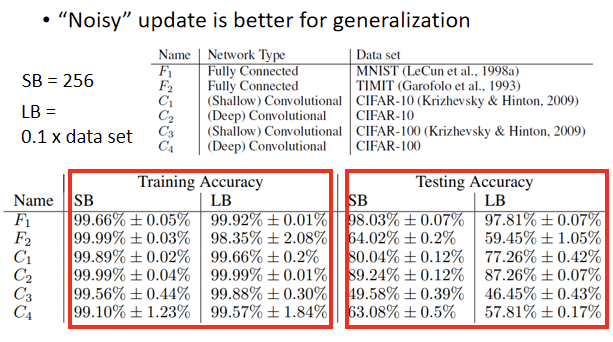
image.png

在这篇Paper里作者Train了六个 Network，裡面有 CNN 的，有 Fully Connected Network 的，做在不同的Cover上，以此来代表这个实验是很泛用的，在很多不同的 Case 都观察到一样的结果，一个小的Batch 里面有256笔Example，大的 Batch(LB，Data Set0。1)有60000笔。 然后将LB跟SB，都训练到差不多的精准度，上表看到的结果是，其实训练大的 Batch 的时候，Training Accuracy 跟小的 Batch，其实是差不多的。 但在Testing 的时候还是很容易就注意到，小的Batch（LB）居然比大的Batch（SB）差，Training 的时候都很好，*Testing 的时候小的 Batch 差，代表 Overfitting，这个才是 Over Fitting ，那為什麼会有这样子的现象呢？在这篇文章裡面也给出了一个解释。

image.png

假设这个是我们的 Training Loss，在上面可能有很多个 Local Minima，这些 Local Minima 它们的 Loss 都很低，即它们 Loss 可能都趋近於 0，但是这个 Local Minima，还是有好 Minima 跟坏 Minima 之分。如果一个 Local Minima 它在一个峡谷裡面，它是坏的 Minima，然后它在一个平原上，它是好的 Minima，為什麼会有这样的差异呢

  • 因為假设现在Training 跟 Testing 中间，有一个 Mismatch，即本来Training 跟 Testing 的 Distribution就不一样，Training 和Testing 的 Loss Function 也不一样。
  • 也可能是因為 Training 跟 Testing都是从 Sample 的 Data 算出来的，也许 Training 跟 Testing sample 到的 Data 不一样，所以它们算出来的 Loss，当然是有一点差距。

那我们就假设说这个 Training 跟 Testing，它的差距就是把 Training 的 Loss，这个 Function 往右平移一点，这时候会发现，对左边这个在一个盆地裡面的 Minima 来说，它的在 Training 跟 Testing 上面的结果，不会差太多，只差了一点点，但是对右边这个在峡谷裡面的 Minima 来说就是天差地远。 很多人相信这个大的 Batch Size，会让结果倾向于走到峡谷裡面，而小的Batch Size，倾向於让参数走到盆地裡面。 直觉上的想法是这样，就是小的Batch size（SB），它有很多的 Loss，它每次 Update 的方向都不太一样，所以如果今天这个峡谷非常地窄，它可能一个不小心就跳出去了，因為每次 Update 的方向都不太一样，它的 Update 的方向也就随机性，所以一个很小的峡谷，没有办法困住小的 Batch，如果峡谷很小，它可能动一下就跳出去，之后停下来如果有一个非常宽的盆地，它才会停下来，那对於大的 Batch Size，反正它就是顺著规定 Update，然后它就很有可能，走到一个比较小的峡谷裡面。 但这只是一个解释，那也不是每个人都相信这个解释，这其实还是一个尚待研究的问题

下图是比较了一下大的 Batch 跟小的 Batch：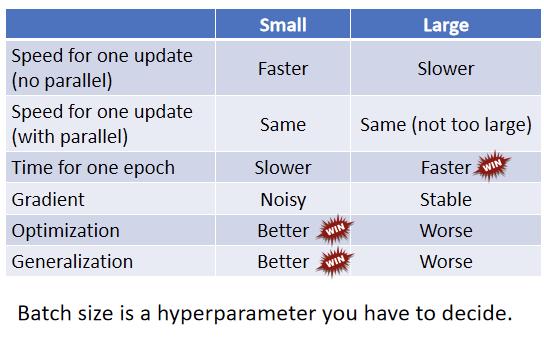
image.png

第一个列是小的Batch，第二个列是大的 Batch 在有平行运算的情况下，小的 Batch 跟大的 Batch，其实运算的时间并没有太大的差距，但是一个 Epoch 需要的时间，小的 Batch 比较长，大的 Batch 反而是比较快的，所以从一个 Epoch 需要的时间来看，大的 Batch 其实有优势的。 而小的 Batch，你会 Update 的方向比较 Noisy，大的 Batch Update 的方向比较稳定，但是 Noisy 的 Update 的方向，反而在 Optimization 的时候会占到优势，而且在 Testing 的时候也会占到优势，所以大的 Batch 跟小的 Batch，各自有它们擅长的地方。

所以Batch Size，变成另外一个需要去调整的 Hyperparameter。

那我们能不能够鱼与熊掌兼得，能不能够截取大的 Batch 的优点，跟小的 Batch 的优点，我们用大的 Batch Size 来做训练，用平行运算的能力来增加训练的效率，但是训练出来的结果又是合适的呢？以下的paper可供阅读。
image.png

Large Batch Optimization for Deep Learning:Training BERT in 76 minutes Extremely Large Minibatch SGD:Training ResNet-50 on ImageNet in 15 Minutes Stochastic Weight Averaging in Parallel:Large-Batch Training That Generalizes Well Large Batch Traning of Convolutional Networks Accurate，large minibatch sgd:Traning imagenet in 1 hour

Momentum

Momentum这是另一个可以对抗Saddle Point，或 Local Minima 的技术。

Small Gradient

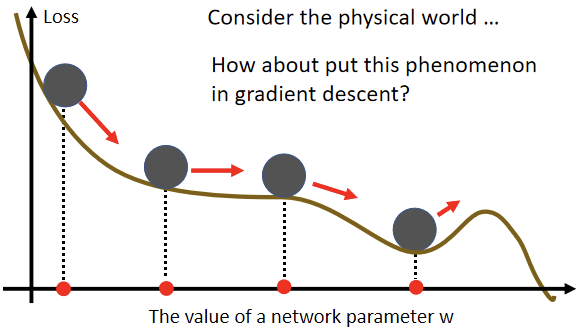
image.png

在物理的世界里，一个球如果从高处滚下来就算滚到 Saddle Point，因为惯性的关系，还是会继续往右走，甚至它走到一个 Local Minima，如果今天它的动量足够大，还是会继续往右走，甚至翻过这个小坡然后继续往右走。即在物理的世界中，一个球从高处滚下来的时候，它并不一定会被 Saddle Point，或 Local Minima卡住，现在就是想办法将这样的概念运用到 Gradient Descent 里呢？（momentum技术）

Vanilla Gradient Descent

（Vanilla直译为香草此处表示一般）
image.png

一般的 Gradient Descent方法，即随机选一个初始的参数叫做四：Batch and Momentum - 图14 ，计算其Gradient，然后往 Gradient 的反方向去 Update 参数： 四：Batch and Momentum - 图15 更新参数以后，再计算一次 Gradient，然后再Update 一次参数直到这个过程无法再继续。

Gradient Descent + Momentum

Momentum在此的应用是，每一次在移动参数的时候，不只是往Gradient的反方向来更新参数，而是Gradient 的反方向，加上前一步移动的方向，即两者加起来的结果，去调整参数。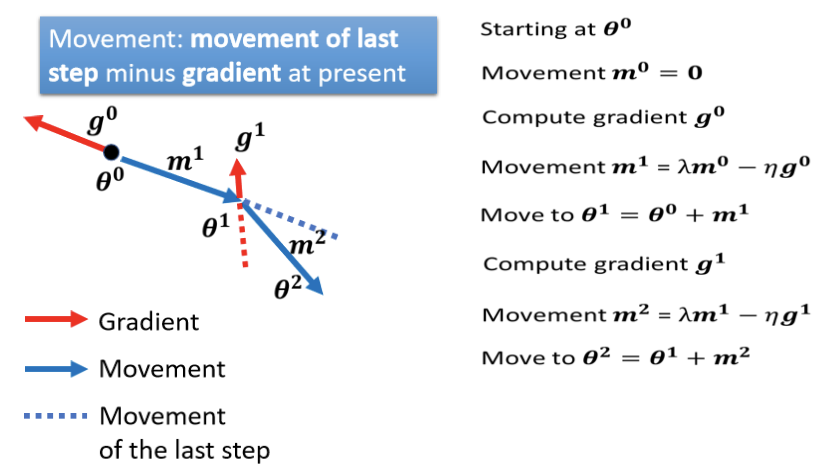
image.png
具体解释为：

  • 一开始找一个初始的参数四：Batch and Momentum - 图17,然后假设前一步的参数的Update量为 0，即movement四：Batch and Momentum - 图18 = 0；
  • 接下来在四：Batch and Momentum - 图19的地方,计算 Gradient 的方向；
  • 接下来下一步更新参数的的方向是 Gradient 的方向加上前一步的方向,不过因为前一步正好是 0,所以 Update 的方向,跟原来的 Gradient Descent 是一样的；

四：Batch and Momentum - 图20

  • 从第二轮开始,加上 Momentum 以后就不太一样了，接下来Update 的方向,不是四：Batch and Momentum - 图21的反方向,而是根据上一次Update方向,也就是 m1 减掉 g1,当做我们新的 Update 的方向。即

四：Batch and Momentum - 图22

见下图：
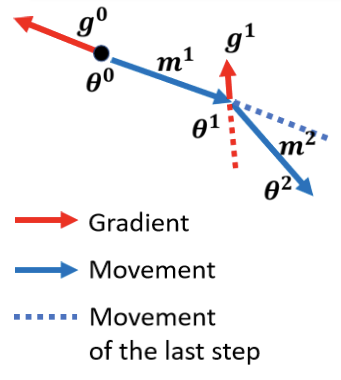
image.png

Gradient表示更新参数要往红色反方向这边走,但是现在不能只凭借Gradient,在加上 Momentum以后,参数更新还需要考虑前一次参数更新的方向：

  • 如果前一次更新方向为蓝色及蓝色虚线四：Batch and Momentum - 图24
  • Gradient表明的方向为红色箭头的反方向四：Batch and Momentum - 图25
  • 把两者相加起来,走两者的折中即θ2这个方向

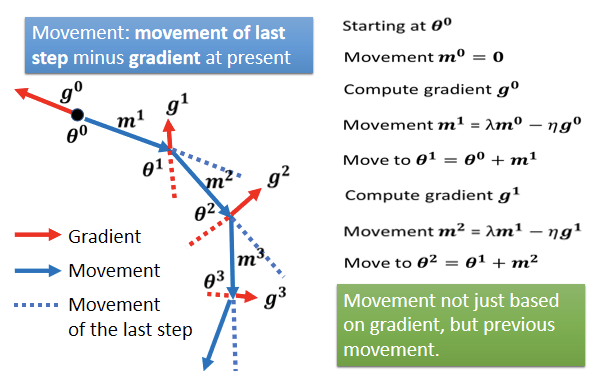
image.pngimage.png
接下来反复进行同样的过程，如上图。
当加上Momentum以后Update的方向,不是只考虑现在的Gradient,而是考虑过去所有 Gradient 的总合.
公式中的λ 是另外一个参数，变成另外一个需要去调整的Hyperparameter。

Concluding Remarks

  • Critical points have zero gradients.
  • Critical points can be either saddle points or local minima.
    • Can be determined by the Hessian matrix.
    • Local minima may be rare.
    • It is possible to escape saddle points along the direction of eigenvectors of the Hessian matrix
  • Smaller batch size and momentum help escape critical points.