感知机与链式法则

感知机（perceptron）

感知机是神经网络的起源算法，在上世纪 50 年代由科学家 Frank Rosenblatt 基于神经感知科学提出。感知机像一个感受器，可接收多个输入信号，输出一个信号。

单层感知机

单层感知机是二分类的线性分类模型，它可以简单地表示为，下面是它的数学模型，其中 sign 激活函数我们之前已经介绍过了，因为它不可导，所以我们接下来使用 sigmoid 激活函数代替 sign 函数。

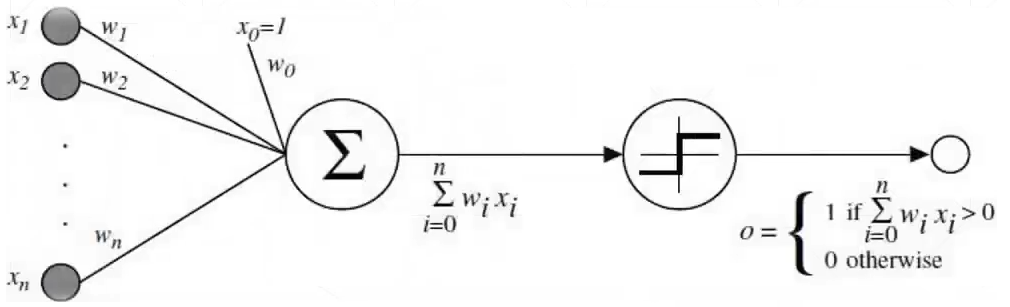
多个输入进入单层感知机，通过加权求和后得到综合值 ，再通过激活函数得到预测值 。通过前面的知识我们知道，我们的目的是要使得损失函数最小，更新 和 参数，进而得到最优的 和 参数。所以下一步，我们利用单层感知机完成一个 和 参数更新操作。

当我们得到预测值 后，通过与真实值 比对，得到损失函数 。这里我们使用常见的均方误差函数，那么 。为了简单起见，我们使用一个训练值举例，也就是只有一个真实值和一个预测值，，乘二分之一的目的是抵消掉求导时产生的 2，加与否无所谓，因为不影响梯度的方向，这样只是便于我们手动计算。

参数更新的公式为 ，这个我们之前接触过， 为输入的参数，已知， 是学习率，已知，唯一不知道的是损失函数 对 的导数。所以，我们要计算 对 的梯度。先求 对 的偏导数，有几个铺陈，以便计算，，。

最终， 对第 个 的偏导数等于 ，、、 都已知，所以 参数可以更新完成。

下面我们使用 pytorch 实现一下。

import torch
from torch.nn import functional as F
lr = 0.1
x = torch.randn(1, 10)
w = torch.randn(1, 10, requires_grad=True)
print(w)
# tensor([[ 1.3171, -0.2054, -1.2400,  0.1385,  0.0743,  0.9640, -0.3430,  0.3459,
#          -0.0509,  0.9320]], requires_grad=True)
o = torch.sigmoid(x @ w.t())  # 计算预测值 o
print(o.shape)  # torch.Size([1, 1])
loss = F.mse_loss(torch.ones(1, 1), o)  # 定义 loss
print(loss.shape)  # torch.Size([])
loss.backward()
print(w.grad)
# tensor([[-0.3915, -0.2115, -0.1993,  0.0623,  0.0919,  0.4512, -0.0347, -0.0664,
#           0.2047,  0.1800]])
w_new = w - lr * w.grad  # 更新 w 参数
print(w_new)
# tensor([[ 1.3562, -0.1843, -1.2200,  0.1323,  0.0651,  0.9189, -0.3395,  0.3526,
#          -0.0713,  0.9141]], grad_fn=<SubBackward0>)

多输出感知机

在上一部分，我们创建了由一个真实值和一个预测值构成的严格意义的感知机。在本部分，我们使用多个真实值和预测值构建多输出的单层感知机，实际上多输出的单层感知机就是神经网络的全连接层中的输出层，它长下面这个样子。

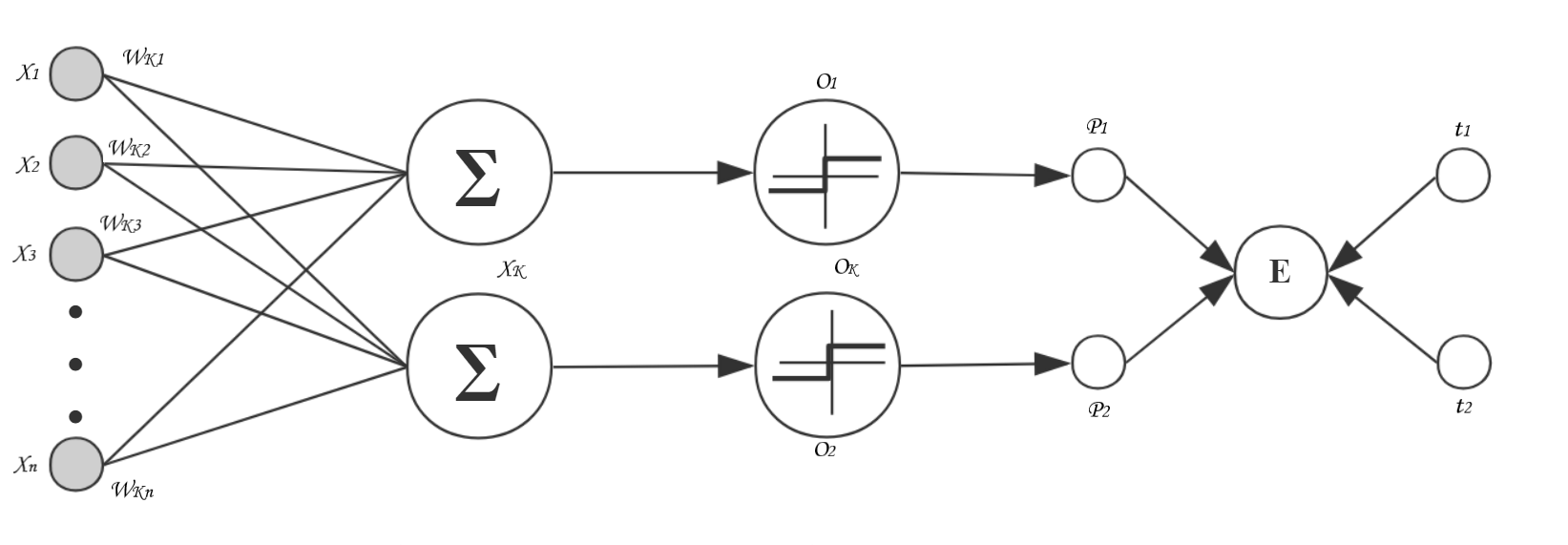
相应的，损失函数就变成了 。重新推导之后， 对第 个分支的第 个 的偏导数等于 。然后我们用 Pytorch 实现一下，实现方法与单输出感知机雷同。

import torch
from torch.nn import functional as F
lr = 0.1
x = torch.randn(1, 10)
w = torch.randn(2, 10, requires_grad=True)
print(w)
# tensor([[-1.0981,  0.4161, -0.9420,  0.1112,  0.8102,  0.3344, -0.6708, -1.4195,
#           0.1471, -0.7545],
#         [-2.3764, -0.5531,  1.1403, -0.4046,  0.0813, -0.4803,  0.3531, -1.2993,
#           0.3948,  0.4814]], requires_grad=True)
o = torch.sigmoid(x @ w.t())  # 计算预测值 o
print(o.shape)  # torch.Size([1, 2])
loss = F.mse_loss(torch.ones(1, 2), o)  # 定义 loss
print(loss.shape)  # torch.Size([])
loss.backward()
print(w.grad)
# tensor([[ 0.0088,  0.0087, -0.0255, -0.0137, -0.0285, -0.0357,  0.0067,  0.0167,
#           0.0043, -0.0181],
#         [ 0.0006,  0.0006, -0.0017, -0.0009, -0.0019, -0.0024,  0.0005,  0.0011,
#           0.0003, -0.0012]])
w_new = w - lr * w.grad  # 更新 w 参数
print(w_new)
# tensor([[-1.0990,  0.4152, -0.9395,  0.1126,  0.8131,  0.3380, -0.6715, -1.4212,
#           0.1467, -0.7526],
#         [-2.3765, -0.5532,  1.1405, -0.4045,  0.0815, -0.4800,  0.3530, -1.2994,
#           0.3947,  0.4815]], grad_fn=<SubBackward0>)

链式法则

一个完备的神经网络不会只含有一层感知机，当我们拥有多层感知机时，怎样将最终的损失函数值一层一层地输出到前面的中间层，以求得损失函数对每一层权值的梯度，更新每一层的参数？这时我们需要用到神经网络中最重要的公式——链式法则。我们在微积分中会经常见到链式法则，实际上在之前的计算中我们已经不经意地用到了这一法则。

我们将 看作是从输入层 x 到输出层 y，中间夹了一层隐藏层 u，若 ，，即 ，那么要求得 的梯度，计算 。如果我们直接将 展开，那么 ，。表面看起来好像链式法则麻烦了些，原因是我们使用了非常简单的函数，并且没有加入激活函数，在实际应用中，链式法则是更高效的，而且通过链式法则，我们可以更清晰地求解各层中的参数。

例如一个最简单的全连接层，它包括一个输入层，一个输出层，一个隐藏层，。那么要求得 E 对输入层中某个参数的偏导数，。一层一层地向前推导，我们就可以清晰地求得每一层中的参数了。

from torch.nn import functional as F
import torch
x = torch.tensor(1.)
w1 = torch.tensor(2., requires_grad=True)
b1 = torch.tensor(1.)
w2 = torch.tensor(2., requires_grad=True)
b2 = torch.tensor(1.)
# 定义 o_1，o_2
o1 = w1 * x + b1
o2 = w2 * o1 + b2
loss = F.mse_loss(torch.tensor(1.), o2)  # 定义 loss
# 定义链式法则
dloss_do2 = torch.autograd.grad(loss, [o2], retain_graph=True)[0]
do2_do1 = torch.autograd.grad(o2, [o1], retain_graph=True)[0]
do1_dw1 = torch.autograd.grad(o1, [w1], retain_graph=True)[0]
dloss_dw1 = torch.autograd.grad(loss, [w1], retain_graph=True)[0]
# 验证
d1 = dloss_do2 * do2_do1 * do1_dw1
d2 = dloss_dw1
print(d1, d2)  # tensor(24.) tensor(24.)

反向传播

我们先来看一个简单的多层多输出的感知机， 为输入层， 为中间层， 为输入层和中间层之间的权重， 表示从输入层的 指向中间层的 的权重，同理， 为输出层， 为中间层与输出层之间的权重， 为中间层 指向输出层 的权重。

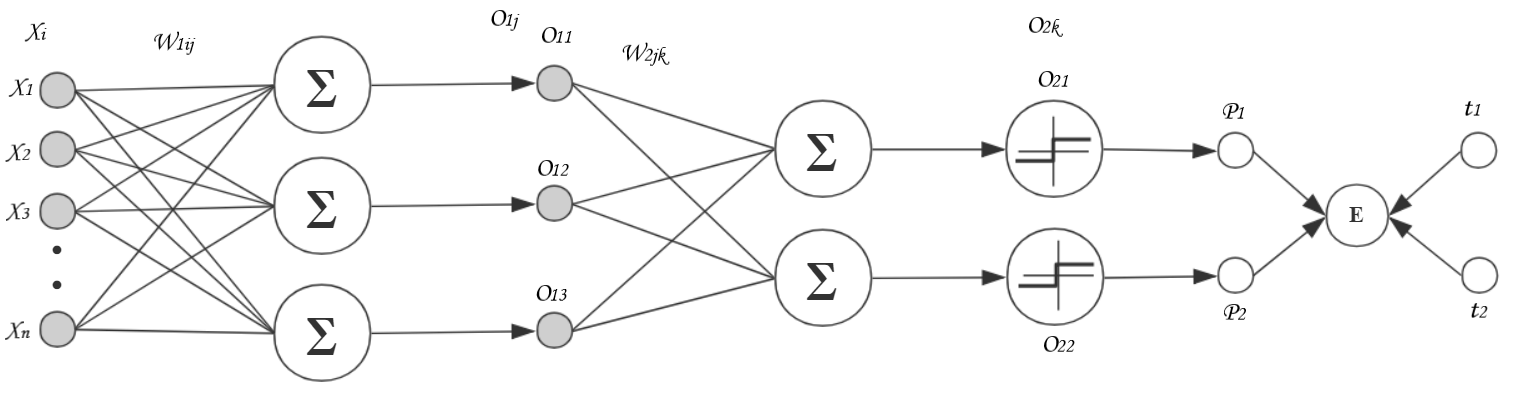
之前多输出感知机的输入层现在变成了多层多输出感知机的中间层 。在之前的单层多输出感知机部分，我们得出过结论，单层多输出感知机的 对第 个分支的第 个 的偏导数等于 。如果把中间层 左边部分挡住，中间层作为输入层，右边部分的偏导数就变成了 。因为 只由 决定，我们把这一部分用一个符号 表示，即 。

接下来，我们推导一下 对 的偏导数。

所以， 对 的偏导数等于 。同样的道理，后半部分 只跟 有关系，所以这一部分我们用符号 代替，即 。

将前面的内容归纳一下，当目标层为输出层时，，。当目标层为中间层（隐藏层）时，，。 是可以直接计算的，所以通过每层的 一层一层地反向传递，就能求得所有层所有权重参数的梯度，进而更新权重参数。