线性回归问题

原理

机器学习的目标是希望从数据中学习到一些高层次的、抽象的概念，对于一个新输入的 x，能够输出一个比较符合实际情况的 y。这样的 y 有两种类型，一种是离散的值，另一种是连续的值。

连续值预测

连续值预测的问题可以归结为给出一个 ，经过模型的函数 f 和参数 θ 给出一个响应 ，使得这个响应尽量逼近真实的 （），最好能够等同于真实的 ，即零误差。

• 一元线性回归就是一个简单的连续值预测问题。

一元线性回归

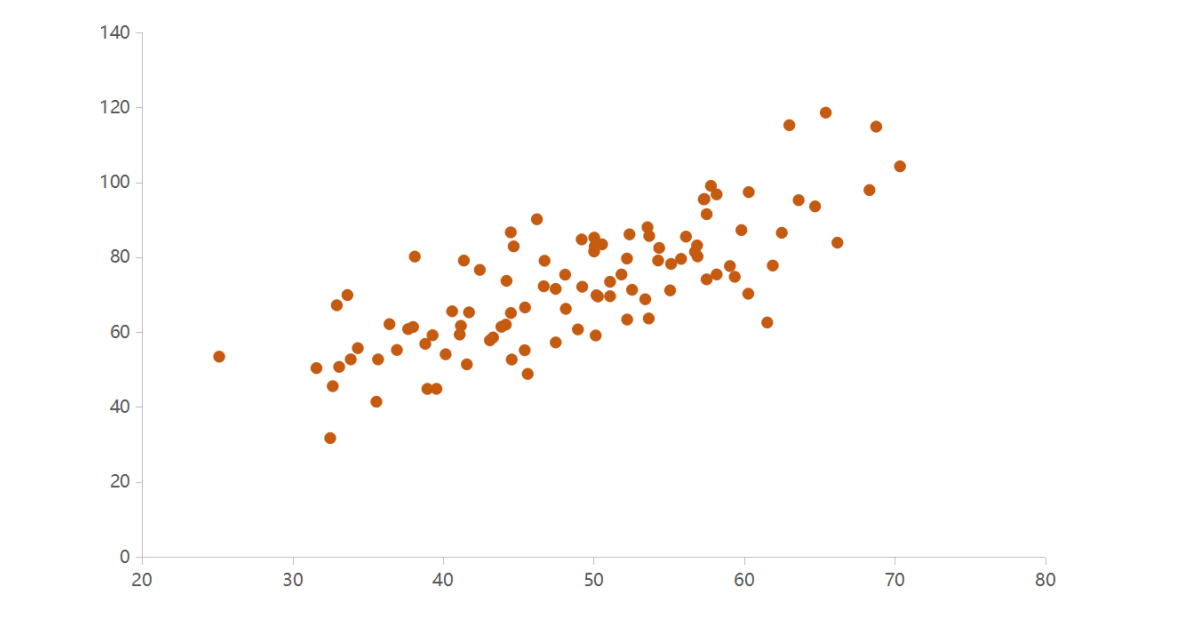
对于 这个方程，我们只需要给出两组数据 和 通过消元法就可以对这个方程精确求解。而日常生活中我们采集到数据的模型通常是未知的，并且数据是有偏差和噪音的。例如下图这组数据，我们可以假设它是符合一元二次方程的分布甚至是更加复杂的方程，也有可能只符合一个简单的一元线性回归。如果它符合 的一元线性回归，我们该如何求解？

损失函数 loss

我们构造一个新的函数叫做损失函数 。之前提到，连续值预测问题的目标是使 尽量逼近于 ，即 。所以我们构造这样一个函数 ， 越小，求得的 和 越精确。为了达到这个目标，我们使用一种梯度下降（Gradient Descent）方法，调优公式如下：

预设 和 的值，每计算一次， 和 都更新一次，即每次 都移动 ， 都移动 ， 衰减因子的作用是减小每次自变量移动的距离。当 的导数小于零，自变量会向右移动，当 的导数大于零，自变量会向左移动，即自变量总是向着 的极小值方向移动，这样最终总能得到一个相对准确的 和 。

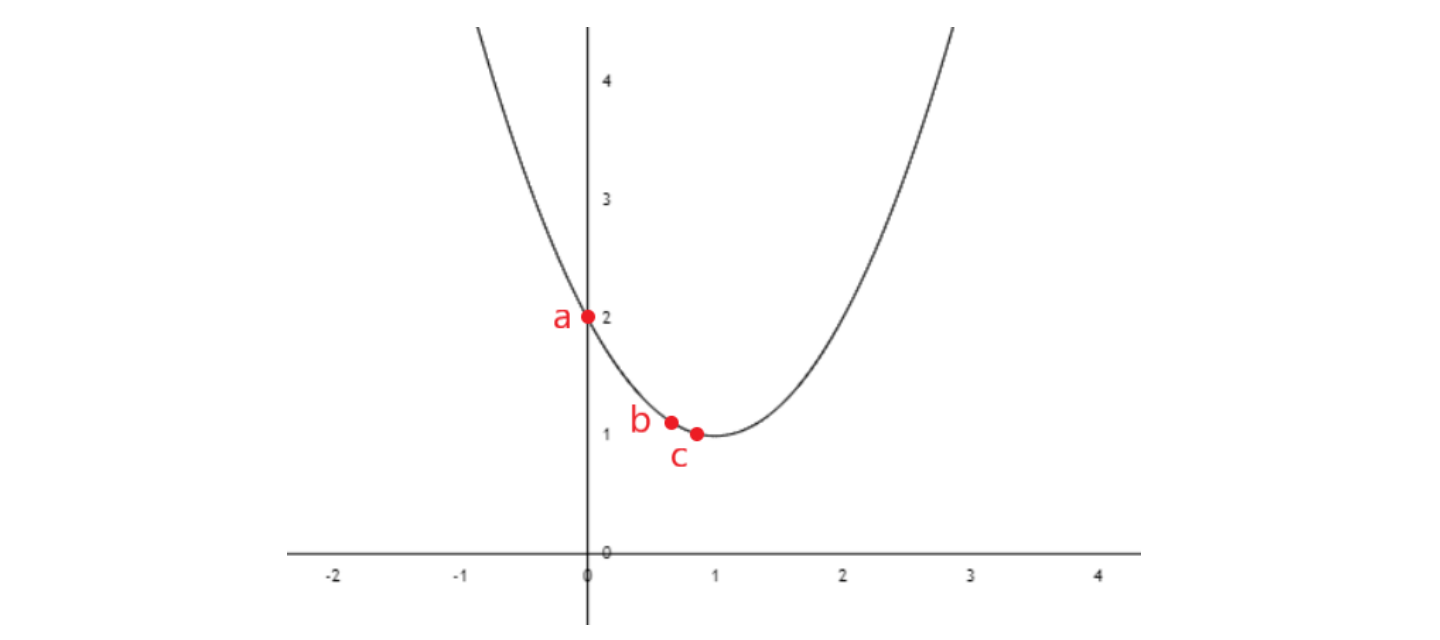
例如我们构造一个易于理解的损失函数 ，图像如下。显然 最小时，。如果使用梯度下降方法，设 初始为 0，衰减因子 ，那么 。第一次计算， 由 0 变为 0.8，最优解会从点 a(0, 2) 移动到点 b(0.8, 1.04)。第二次计算， 由 0.8 变为 0.96，最优解从点 b(0.8, 1.04) 移动到点 c(0.96, 1.0016)，越来越趋近最优解。虽然该方法对于这种明确有可求边界的函数略显复杂，但对于求解模糊复杂函数的最优解是很有帮助的。

实现

在上一部分我们提到，求解一个线性回归问题，要使得 ，这里的 是输入的自变量， 是真实的输出。首先要构造一个损失函数 ，不断地调整 和 使损失函数达到最小，数据量较大时，损失函数一般会取 ， 为点的个数，即 。然后通过梯度下降方法构造 和 的调优公式，每次计算出新的 和 都使损失函数 向最小值趋近一小步，最后我们的目标就变成了求解损失函数的最小值，从而取得最优的 和 。我们分别使用 Numpy 和 Pytorch 来实现。

Numpy 实现

# # 导入 numpy 库
import numpy as np
# # 求解 y = wx + b，定义 loss 函数
# 参数 b 和 w 分别为偏秩和斜率，points 为点的数组 [(x0,y0),(x1,y1),……,(xn,yn)]
def ComputeLossforLineGivenPoints(b, w, points):
    totalLoss = 0
    N = float(len(points))
    for i in range(0, len(points)):
        # 这是 numpy 一种特殊的数组取值方法，等同于 points[i][0]
        x = points[i, 0]
        y = points[i, 1]
        # 计算 (w * x + b - y) 的平方和
        totalLoss += (w * x + b - y) ** 2
    # 损失函数 loss 取 1/N
    return totalLoss / N
# # 定义 gradient descent 算法
# b_current 和 w_current 是上一次调优的 b 和 w，learningRate 是衰减因子 lr
def SetGradientDescent(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # loss 对 b 的偏导数求和
        b_gradient += (2/N) * ((w_current * x + b_current) - y)
        # loss 对 w 的偏导数求和
        w_gradient += (2/N) * x * ((w_current * x + b_current) - y)
    # 更新调优的 b 和 w
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]
# # 定义循环函数，不断地优化 b 和 w
# starting_b 和 starting_w 为预设的偏秩和斜率，num_iterations 是循环的次数
def GradientDescentRunner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    # 不断地执行 gradient descent 算法
    for i in range(num_iterations):
        b, w = SetGradientDescent(b, w, np.array(points), learning_rate)
    return [b, w]
def Run():
    # 这里使用一个随机的数据集，共有100个点，即本节第一张图所示的数据
    points = np.genfromtxt("data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0 # 预设的偏秩
    initial_w = 0 # 预设的斜率
    num_iterations = 1000 # 设置循环1000次
    # 打印调优之前的 b、w 和误差
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b, initial_w,
                  ComputeLossforLineGivenPoints(initial_b, initial_w, points))
          )
    print("Running...")
    # 得到最优的 b 和 w
    [b, w] = GradientDescentRunner(points, initial_b, initial_w, learning_rate, num_iterations)
    # 打印调优之后的 b、w 和误差
    print("After gradient descent b = {0}, w = {1}, error = {2}".
          format(b, w,
                 ComputeLossforLineGivenPoints(b, w, points))
          )
if __name__ == '__main__':
    Run()
# # 结果
# Starting gradient descent at b = 0, w = 0, error = 5565.107834483211
# Running...
# After gradient descent b = 0.08893651993741346, w = 1.4777440851894448, error = 112.61481011613473

Pytorch 实现

import numpy as np
import torch
import torch.nn as nn
from torch import optim
from torch.autograd import Variable
points = np.genfromtxt("data.csv", delimiter=",")
x_train = points[:, :1]
x_train = x_train.astype(np.float32)
y_train = points[:, 1:]
y_train = y_train.astype(np.float32)
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)  # 输入和输出都是一维
    def forward(self, x):
        out = self.linear(x)
        return out
model = LinearRegression()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.0001)
num_epochs = 1000
for epoch in range(num_epochs):
    inputs = Variable(x_train)
    target = Variable(y_train)
    # 前向传播
    out = model(inputs)
    loss = criterion(out, target)
    # 后向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
print("Running...")
# 得到最优的 b 和 w
[w, b] = list(model.parameters())
b = b.tolist()
w = w.tolist()
# 打印调优之后的 b、w 和误差
print("After gradient descent b = {0}, w = {1}, error = {2}".
     format(b, w,
            loss.item())
     )
# # 结果
# Running...
# After gradient descent b = [0.792700469493866], w = [[1.463911771774292]], error = 112.21363067626953