导数与梯度

梯度（gradient）

什么是梯度

我们先从导数说起，一个函数的导数定义为函数在自变量 处的变化量，导数代表了在自变量变化趋于无穷小的时候，函数值的变化与自变量变化的比值，即 ，几何意义为某点切线的斜率，物理意义为某时刻的变化率，因此导数是标量。

在一元函数中，只有一个自变量变动，所以函数只有一个方向的导数。当函数变为多元，多个自变量同时变动，函数就有了多个方向的导数，这时就产生了偏导数的概念。对于一个二元函数，它的几何形状是一个空间曲面，对于面上的一个点来说，它有无穷多个方向可以变化，也就是说二元函数有无穷多个导数，但是它只有两个偏导数。也就是说，偏导数是函数在各个自变量方向上的导数，它们也是标量。例如函数 ， 对 的偏导数 ， 对 的偏导数 。

梯度的定义就是函数所有的偏导数组成的向量，即 ，上述函数 的梯度则表示为 ，梯度的大小也就是梯度的模等于 。

梯度有什么用

在求解线性回归问题时，我们构造了损失函数。在这个过程中，沿着函数梯度下降的方向，我们可以找到损失函数的最小值，从而求得线性回归问题的最优解。而且，对于某个特定的点来说，梯度的方向是函数在该点变化最快的方向，好比一个小球在半球形的碗的边缘自由下滑，一定会按照一个时刻受力最大的轨迹移动（当然具体情况可能会复杂得多）。

以函数 为例，当 、 到达 时，函数在某个方向上的变量的增量设为 ，并设置 方向的单位向量为 ，那么 在 轴上的投影为 ， 在 轴上的投影为 。这样的话，函数 在 方向上的增量 就等于 ，那么函数 在 处的导数就可以表示为 现在我们设一个 向量为 ， 向量为 ，两者的夹角为 ，那么 就可以表示为 ，要想 达到最大， 等于 0，即两者平行。那这样 的最大值就等于 ，所以梯度的方向是函数在 点变化最快的方向。

梯度下降算法

为了沿着函数梯度下降的方向找到损失函数的最小值，我们需要构造梯度下降算法来优化参数，这一部分在线性回归问题求解时已详细阐述，这里只列出公式：

梯度下降的问题

对于凸函数（函数上任意两点之间拉一条直线，这条直线上的任一点的值都要大于它在原函数上投影的点的值，类似于半球形），它总是能找到一个全局最优解，所以上面的这些方法是很完美的。然而对于非凸的，也就是坑坑洼洼的函数来说，一个全局最优解并不容易找到。能否顺利找到最优解取决于参数的初始状态（参数初始值在函数中的位置）、学习率（决定参数位置移动的步长）、动量（函数达到极小值而非最小值时，能否冲出极小值的束缚）。

损失函数

MSE 函数

非常常见的损失函数有均方误差函数（Mean Squared Error，MSE）、交叉熵函数（Cross Entropy），在这里我们重点阐述均方误差函数及其实现，交叉熵函数留到逻辑回归问题部分。在手写数字体识别问题中，我们接触到了均方误差函数 。我们在 Pytorch 进阶操作中提到过二范数，均方误差函数等于 的二范数的平方，即 。

接下来，我们要使用 pytorch 实现 MSE 损失函数的定义和求导。求导有两种方式，手动求导和自动求导。要注意的是，因为 pytorch 是动态图，也就是做一步计算一步图，每次求导更新参数后，图也要手动更新一遍，具体问题在代码中展示。

Pytorch 实现

import torch
from torch.nn import functional as F
x = torch.ones(1)
w = torch.full([1], 2)
b = torch.full([1], 1)
# y = wx + b
mse = F.mse_loss(x*w+b, torch.ones(1))
# loss = sum((pred - y)^2)
# 设定 w 和 b 是可导的
w.requires_grad_()
b.requires_grad_()
# 我们也可以在定义 w 或 b 时直接设定可导，w = torch.full([1], 2, requires_grad=True)
# torch.autograd.grad(mse, [w, b])
# RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
# 因为设定 w 和 b 可导是在 loss 定义后，所以在改变 w 和 b 后需要重新定义 loss，否则报错
mse = F.mse_loss(x*w+b, torch.ones(1))
# torch.autograd.grad() 用于手动计算 loss 对各参数的偏导，返回偏导列表
d = torch.autograd.grad(mse, [w, b])
print(d)  # (tensor([4.]), tensor([4.]))
# 验证一下，dmse/dw=2(1-(wx+b))(-x)=4，dmse/db=2(1-(wx+b))(-1)=4
x1 = torch.ones(1)
w1 = torch.full([1], 2, requires_grad=True)
b1 = torch.full([1], 1, requires_grad=True)
mse1 = F.mse_loss(x1*w1+b1, torch.ones(1))
# 直接在 loss 函数上使用 backward 就可以自动计算 loss 对所有参数的偏导
mse1.backward()
# 我们可以查看 loss 对每个参数的偏导
print(w1.grad)  # tensor([4.])
print(b1.grad)  # tensor([4.])

激活函数

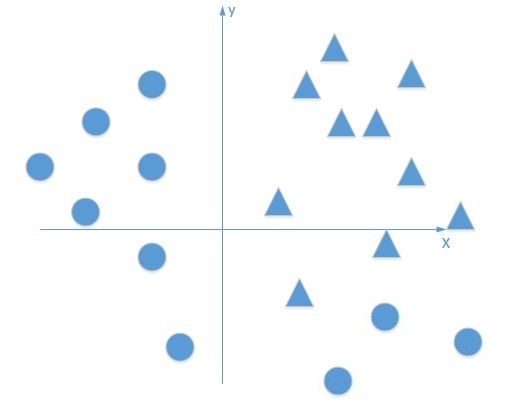
在求解手写数字体问题的时候，我们为了将回归模型复杂化，添加了一个非线性因子，也就是激活函数。它的作用是为了让原本线性的模型变得非线性化，比如说下图的二分类问题，如果我们用单层感知机在两个类别之间划一条界线，那只能画一条直线，但没有一条直线能够清晰地将两种类别分离开。这时，我们需要通过激活函数让神经网络能够拟合一条曲线来清晰地将两种类别分离。

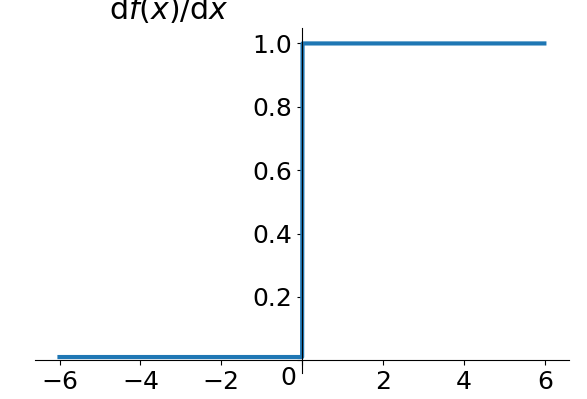
最初的激活函数 sign 来源于青蛙的神经元机制，当输入的值达到神经元打开的阈值，神经元才会被激活，否则，神经元处于关闭状态，于是产生了下面这种阶梯函数。当 x 小于 0 的时候，函数值等于 0，x 大于 0 时，函数值为大于 0 的恒定值。但是，这种激活函数是不连续的，当 x 等于 0 时，函数不可导。

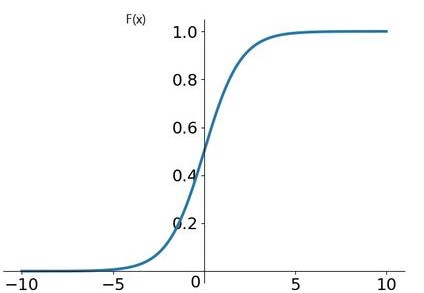
Sigmoid 函数

为了解决阶梯函数不可导的问题，科学家提出了一种连续的、平滑的 Sigmoid 激活函数，。它的最小值接近于 0，最大值接近于 1，且越靠近最大值或最小值，梯度越平缓。

我们推导一下它的导数：

所以 ，因为 的取值为 (0, 1)，所以 sigmoid 函数的导数也被限定在了 (0, 1) 的范围内。神经网络经常会用到这样一个范围，比如概率的表示，RGB 通道的表示等等，所以 sigmoid 函数是非常有用的。 但 sigmoid 函数也有一个缺陷，当自变量 x 的绝对值比较大时，会出现导数更新速度非常慢的情况，这种现象叫做梯度离散。

a = torch.linspace(-100, 100, 10)
print(a)
# tensor([-100.0000,  -77.7778,  -55.5556,  -33.3333,  -11.1111,   11.1111,
#           33.3333,   55.5555,   77.7778,  100.0000])
b = torch.sigmoid(a)
# tensor([0.0000e+00, 1.6655e-34, 7.4564e-25, 3.3382e-15, 1.4945e-05, 9.9999e-01,
#         1.0000e+00, 1.0000e+00, 1.0000e+00, 1.0000e+00])
print(b)

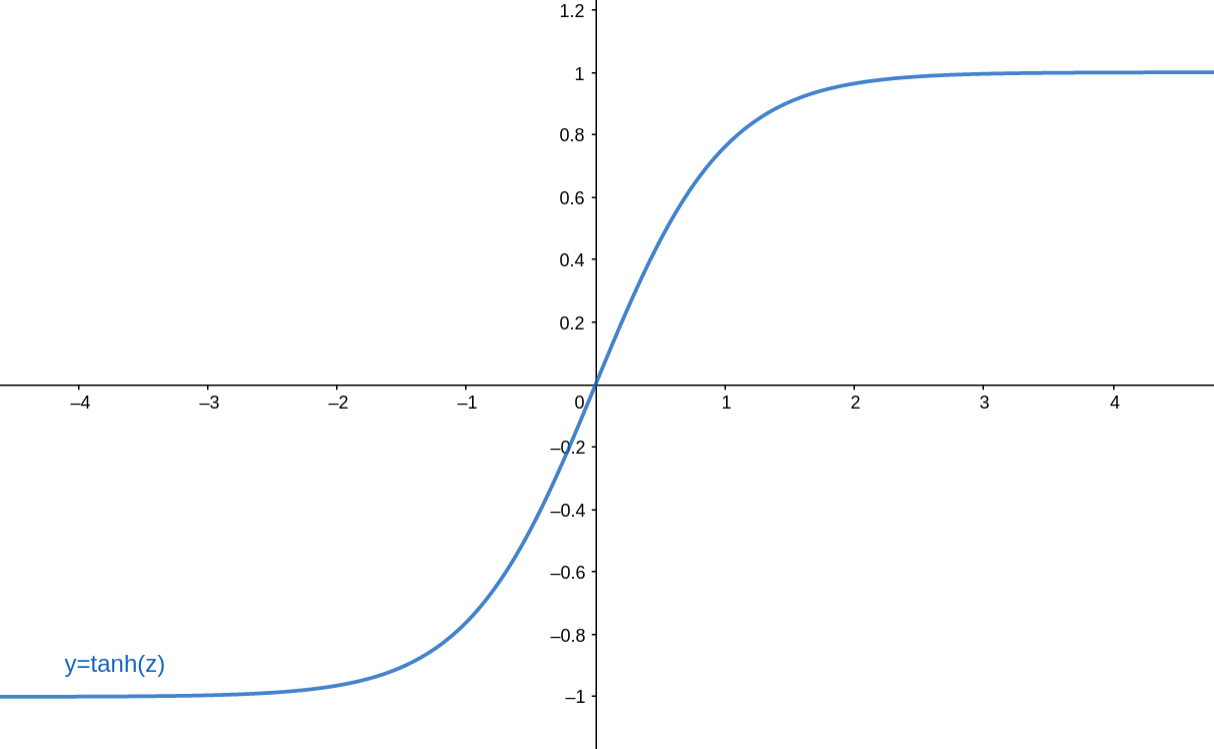
Tanh 函数

Tanh 函数是另一种激活函数，它是 sigmoid 函数的变形，在循环神经网络（Recurrent Neural Network）中经常被使用。，也就是在 sigmoid 函数的基础上，横坐标缩小一倍，纵坐标扩大一倍，然后减一，出来就是下面这个样子。

同样推导一下它的导数：

c = torch.linspace(-1, 1, 10)
print(c)
# tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111,  0.1111,  0.3333,  0.5556,
#          0.7778,  1.0000])
d = torch.tanh(c)
print(d)
# tensor([-0.7616, -0.6514, -0.5047, -0.3215, -0.1107,  0.1107,  0.3215,  0.5047,
#          0.6514,  0.7616])

ReLU 函数

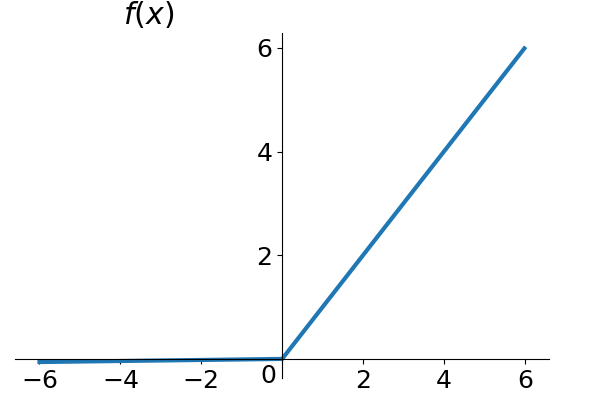
ReLU 函数是一个非常简单的激活函数，但也是目前神经网络中用的最多的激活函数，ReLU 全称 Rectified Linear Unit（整形线性单元）。当 x 小于零的时候，ReLU 函数不响应，当 x 大于等于零的时候，ReLU 函数线性响应。

ReLU 函数的优势在于它的导数计算起来非常简单，并且不容易出现梯度离散或梯度爆炸现象，它长这个样子：

e = torch.linspace(-8, 8, 10)
print(e)
# tensor([-8.0000, -6.2222, -4.4444, -2.6667, -0.8889,  0.8889,  2.6667,  4.4444,
#          6.2222,  8.0000])
f = torch.relu(e)
print(f)
# tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.8889, 2.6667, 4.4444, 6.2222,
#         8.0000])

还有一个比较常用的激活函数叫做 ，它经常和交叉熵损失函数一同使用，所以 softmax 函数同交叉熵函数一起留到逻辑回归问题部分。