手写数字体识别

原理

机器学习的目标是希望从数据中学习到一些高层次的、抽象的概念，对于一个新输入的 x，能够输出一个比较符合实际情况的 y。这样的 y 有两种类型，一种是离散的值，另一种是连续的值。

离散值预测

离散值的预测问题以分类问题为主，给出一个 x，经过模型的函数 f 和参数 θ 给出一个基于所有目标值的单位向量响应 ，使得这个单位向量中真实的 对应的数值最大，即最有可能的结果是 。

• 离散值预测以分类问题为主，例如手写数字体识别问题。

MNIST 数据集

首先我们来介绍一个常用的数据集 MNIST，它是由 Yann Lecun 收集得到的，Yann Lecun 是卷积神经网络的发明者，他被称为深度学习的三驾马车之一，另外两位分别是“AI 圣经”《Deep Learning》的作者 Yoshua Bengio 与 神经网络之父 Geoffrey Hinton。

MNIST 包含了从 0 到 9 十种数字各 7000 张图片，每张图片采集于不同的人的不同笔迹，总共有 70k 张图片。我们将 70k 张图片分为 60k 的训练集和 10k 的测试集，训练集用于得出 和 ，测试集用于测试模型的性能。

标准化处理

像素标准化

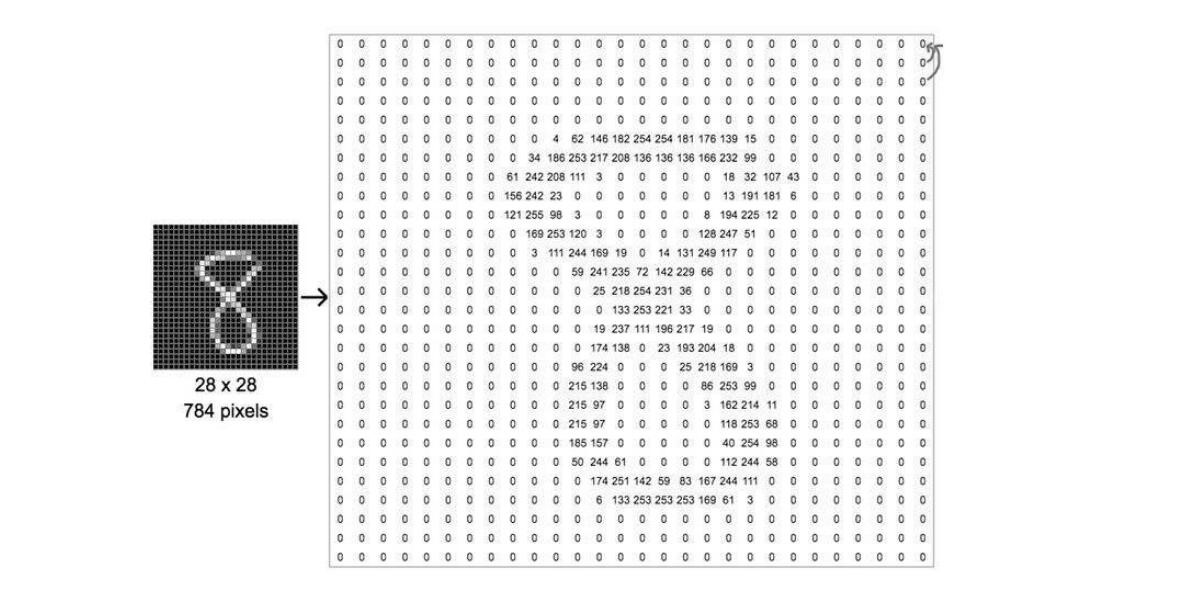
对于图片的分类问题，输入图片的大小和长宽比都是不定的，为了解决这个问题，我们将手写数字图片标准化为 28*28 的像素（图2），用 0~255 的数字表示像素的灰度值，0 表示像素颜色为纯黑，255 表示像素颜色为纯白。这样的话我们就可以将输入图片的形状记为 [28, 28, 1]，28 行 28 列 1 个值。若图片为彩色，我们可以使用表示 RGB 的元组 (0~255, 0~255, 0~255) 填充像素，输入图片的形状记作 [28, 28, 3]，28 行 28 列 3 个值。

为了取得一张图片的向量，我们将图片像素值的每一行依次追加到第一行之后，形成一个长度为 784 的向量，记作 [1, 784] 作为输入向量，这里的 1 代表输入一张图片，[a, 784] 则代表输入 a 张向量长度为 784 的图片。

One-hot 编码

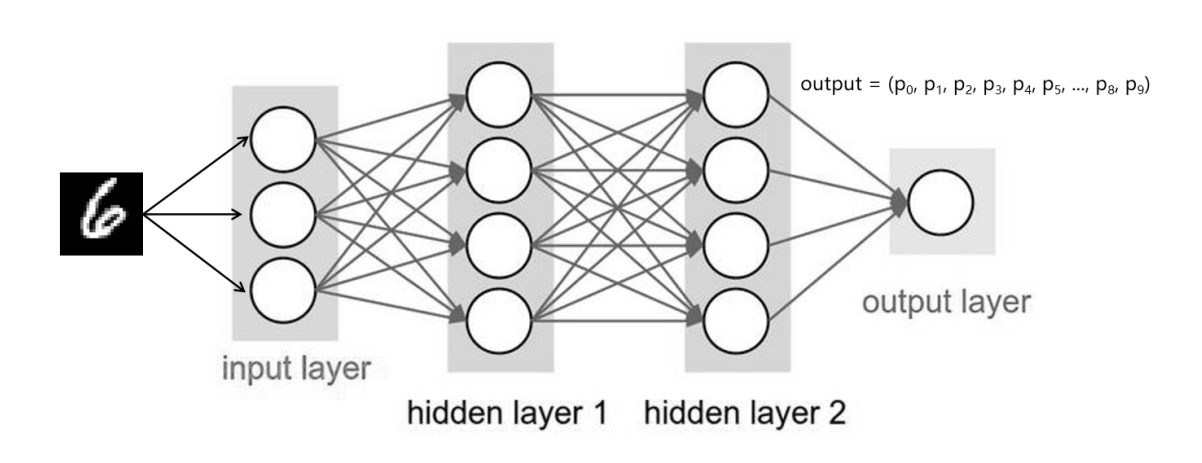
我们最终想要得到一种输出结果，它能够显示出哪种类别的可能性最高。我们介绍一种 One-hot 编码方式，假设问题中总共有 n 个类别，输出结果可以表示为 的向量，下标为 的元素代表第 种类别的概率，所有类别的概率相加等于 1，即 。如图 3 中输入数字 6 的图片，经过模型训练后输出一组向量，， 应为最大元素。

回归问题的复杂化

如果我们把分类问题中的每个类别看做一个回归问题，那输出向量中的每个元素都是一个回归问题的解。将回归问题的解法迁移到分类问题上，分类问题的目标就变成了求解 。对于手写数字识别问题，output 是长度为 10 的向量，即 110 的矩阵，input 是一个长度为 784 的向量，即 1784 的矩阵。 对应十种数字的回归问题的偏秩，所以也是长度为 10 的向量，即 110 的矩阵。将它们代入公式可以得出 是一个 78410 的矩阵。

求解分类问题只需要一个简单的线性回归模型就可以了吗？显然不行。一个分类模型内部的逻辑是复杂的的，不太可能是一个线性的逻辑。那怎么办呢？我们在回归模型上添加一个非线性因子，它是一个函数，添加后变成这个样子 。我们把 函数称为激活函数，这个函数有一个简单常见的形式叫做 ReLU 函数，那么我们的模型就变成 。

隐藏层

即使这样，经过测试发现这个模型还是太简单了，准确度并不高。所以一道工序不行再加一道，也就出现了深度学习中的隐藏层 hidden layer。首先，将 input 传入第一个隐藏层：，然后将第一个隐藏层的输出 作为 input 传入下一个隐藏层：，然后不断地重复，最终输出层输出 。

现在我们使用三道工序求解手写数字识别问题，input 是 1784 的矩阵，， 可以是 784512 的矩阵， 可以是 1＊512 的矩阵，， 可以是 512256 的矩阵， 可以是 1256 的矩阵，， 可以是 25610 的矩阵， 可以是 110 的矩阵。可以发现，输入 input 和输出 output 的形状都是给定的，中间过程里 和 的形状满足数学运算就可以了。

均方误差函数

下面我们来构建模型的损失函数 来优化参数 。对于 6 这个数字来说，它的真实的 应该等于 (0, 0, 0, 0, 0, 1, 0, 0, 0, 0)，但我们的输出 ouput 里并不一定只有一个元素 1，它有可能是这个样子：(0, 0, 0, 0, 0, 0.8, 0, 0.05, 0.15, 0)，我们希望输出 output 更接近真实的 。所以我们计算一个均方误差函数（MSE）作为损失函数 ，即 。

实现

上述部分中，我们将线性回归的方法迁移到分类问题，使用 ReLU 函数给模型添加非线性因子，然后加入隐藏层，计算每层中的 、 和 output，将每层的 output 作为下一层的 input，不断重复。使用均方误差函数（MSE）构建损失函数 ，对所有的 和 进行调优。

Matplotlib 可视化

import  torch
from    matplotlib import pyplot as plt
def plot_curve(data):
    fig = plt.figure()
    plt.plot(range(len(data)), data, color='blue')
    plt.legend(['value'], loc='upper right')
    plt.xlabel('step')
    plt.ylabel('value')
    plt.show()
def plot_image(img, label, name):
    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(img[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')
        plt.title("{}: {}".format(name, label[i].item()))
        plt.xticks([])
        plt.yticks([])
    plt.show()
def one_hot(label, depth=10):
    out = torch.zeros(label.size(0), depth)
    idx = torch.LongTensor(label).view(-1, 1)
    out.scatter_(dim=1, index=idx, value=1)
    return out

Pytorch 实现

import  torch
from    torch import nn
from    torch.nn import functional as F
from    torch import optim
import  torchvision
from    utils import plot_image, plot_curve, one_hot

batch_size = 512
# # 加载 Mnist 数据集
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=False)

x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), x.max())
# 展示数据样例
plot_image(x, y, 'image sample')
# # 定义训练模型
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # wx + b
        self.fc1 = nn.Linear(28*28, 256)
        self.fc2 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        # x: [b, 1, 28, 28]
        # h1 = relu(xw1 + b1)
        x = F.relu(self.fc1(x))
        # h2 = relu(h1w2 + b2)
        x = F.relu(self.fc2(x))
        # h3 = h2w3 + b3
        x = self.fc3(x)
        return x

net = Net()
# [w1, b1, w2, b2, w3, b3]
# 使用 optimizers 类可以简单地定义梯度下降函数 x' = x - lr * δloss/δx
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []
# # 定义 loss 与 gradient descent
for epoch in range(3):
    for batch_idx, (x, y) in enumerate(train_loader):
        # x: [b, 1, 28, 28], y: [512]
        # [b, 1, 28, 28] => [b, 784]
        x = x.view(x.size(0), 28*28)
        # => [b, 10]
        out = net(x)
        # [b, 10]
        y_onehot = one_hot(y)
        # loss = mse(out, y_onehot)
        loss = F.mse_loss(out, y_onehot)
        optimizer.zero_grad()
        loss.backward()
        # w' = w - lr*grad
        optimizer.step()
        train_loss.append(loss.item())
        if batch_idx % 110 == 0:
            print(epoch, batch_idx, loss.item())
plot_curve(train_loss)
# we get optimal [w1, b1, w2, b2, w3, b3]
total_correct = 0
for x, y in test_loader:
    x = x.view(x.size(0), 28*28)
    out = net(x)
    # out: [b, 10] => pred: [b]
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct += correct
total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)
x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')

# # 结果
# 0 0 0.10349637269973755
# 0 110 0.049387287348508835
# 1 0 0.04749932512640953
# 1 110 0.03771667554974556
# 2 0 0.035466525703668594
# 2 110 0.03215049207210541
# test acc: 0.887