1.element-wise operations(逐点运算)

  • 相同维度的张量可以进行逐点运算，比如：+-*/等。并且运算是作用在相同位置的元素。

    2.broadcast(广播机制)：让不同维度的张量进行逐点运算

    1. x = np.random.random((4,5)) * 10
    2. x

  • np.random.random():产生0~1之间的浮点数。

  • np.random.random((4,5))：使用0~1之间的浮点数组成(4,5)形状的张量。

  • np.random.random((4,5)) 10：每一个数的数值都10，同样是**(4,5)形状的张量。**

    1. y = np.random.random(5) * 10
    2. y

  • y的shape:(5,)

    1. #先借助广播机制将y变为(4，5)的，然后进行逐点比较
    2. z = np.maximum(x,y)
    3. z

  • np.maximum(x,y):逐点运算，比较x,y的每一个位置的最大值

  • 先借助广播机制，将y先变成(4，5)的，每一行都是原来的y

  • 然后进行逐点比较

    3.对2d tensors进行按列/按行操作

    按列对其进行加和

    1. x = np.random.randint(30,size=(2,4))
    2. x
    1. y = x.sum(axis=0)
    2. y

  • axis=0表示按照列加和

  • y轴就是”第0轴”

image.png
想要知道原来x的每一行各位置元素占对应列和的百分数，则可以直接用”/“

  1. z = x / y
  2. z

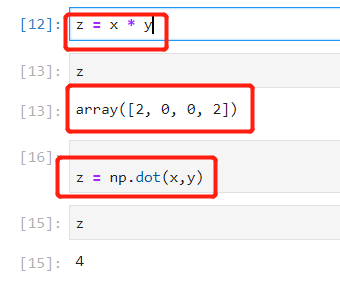
image.png

4.np.dot()运算符

  • 使用numpy去计算向量的乘法会降低运算时间。

情况①：向量*向量===逐点相乘，再相加
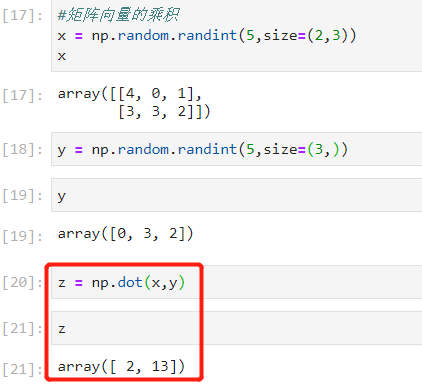
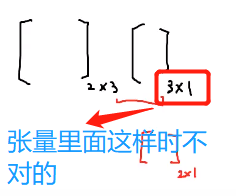
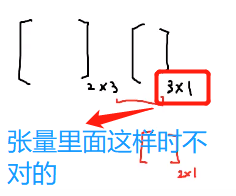
image.png image.png
情况②：矩阵*向量
image.png image.pngimage.png

  • python里面的矩阵和向量相乘，不能将向量看成3*1的，而是(3，)。
  • 但是计算过程是类似的，最终的结果也是一样的

情况③：矩阵*矩阵：和平常的一样
情况④：高维度的dot运算：（a,b,c,d）dot (d,e) = (a,b,c,e)
（a,b,c,d）dot (d,) = (a,b,c)[后面的逗号省略]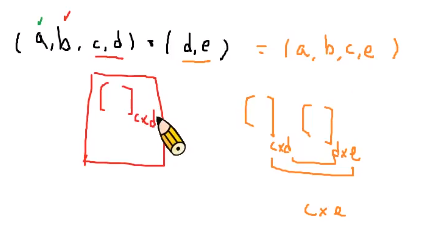
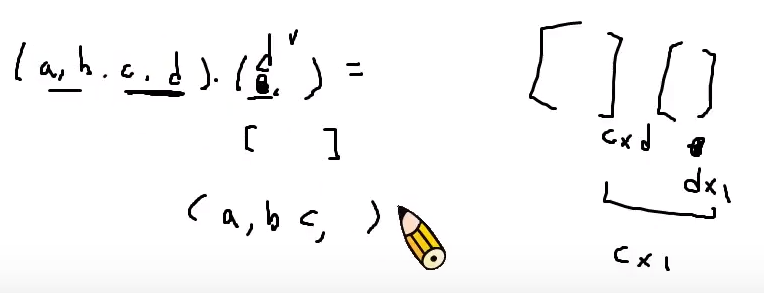
image.pngimage.png

  • 都是先看低纬度的计算，高纬度保留
  • python里面的向量都是横着摆的，计算的时候可以先将其摆成数学中的竖着的，最后再变过来

  • 从后往前算

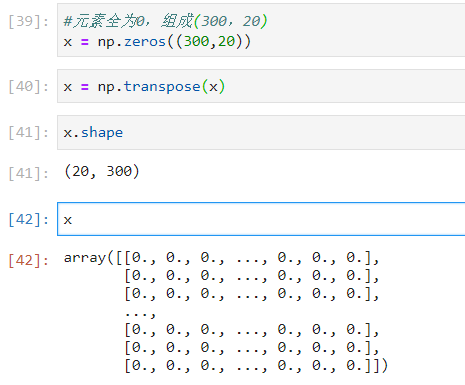
    5.np.reshape()运算符

  • np.zeros(size):组成指定size的张量，并且所有元素的值都是0.

  • np.transpose():对张量进行转置运算.

image.png

6.高维张量的转置怎么转置呢？以及如何写出来高维张量的转置？

  • 高纬度的张量的转置都是将各个维度的值**倒过来写**。
  • (3,20,100)的转置是(100,20,3)

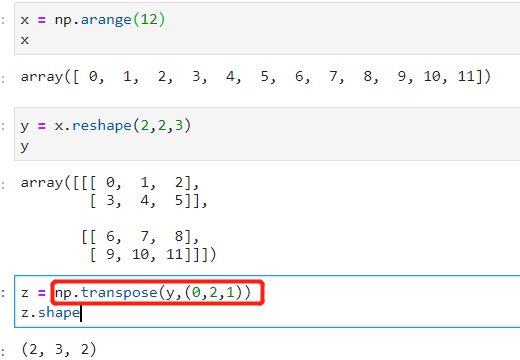
step1：借助np.arange()构造(24，)的x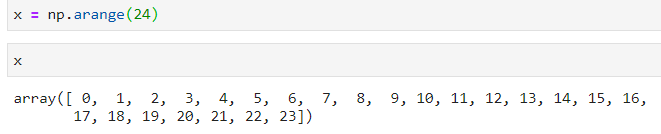
image.png
step2：借助np.reshape(2,3,4)将x变为(2,3,4)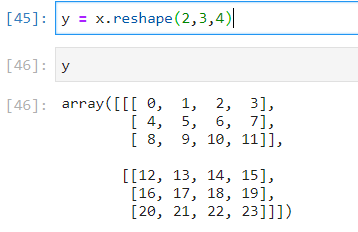
image.png
step3：对y进行转置运算，看z的具体取值情况
image.png image.png

  • （2，3，4）——>（4，3，2）：相当于将第0轴与第2轴进行交换.
  • 首先已经确定z的形状是(4，3，2)，现在的目标是往对应位置进行填数。

image.png

  • 找到z中元素的索引下标，按照轴对换的规则进行对换，然后再到y里面去找相应的元素。

    7.对张量不全部转置而是部分转置的做法！(在transpose函数后面加上指定即可)

    image.png

  • z即是将y的第1轴和第2轴交换的结果，想要写出z的具体取值，和上面的方法一样