1.三种随机梯度下降的方式(true SGD、minibatch SGD、batch SGD)

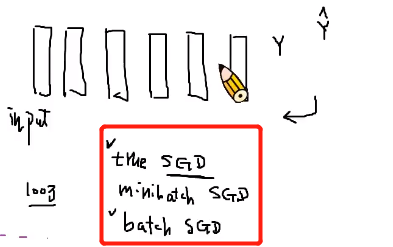
image.png

  • 比如目前有100万个数据
  • true SGD：每次丢进去1个数据，然后就进行反向传递，更新参数
  • batch SGD:一次性把所有的100万个数据全部丢进去，然后更新参数
  • minibatch SGD:一次丢一批数据，然后就进行反向传播，更新参数

  • minibatch SGD效果一般最好，前两种太过极端

    2.反向传播的原理总结

  • 梯度的方向就是变量变化最快的方向的简答说明：

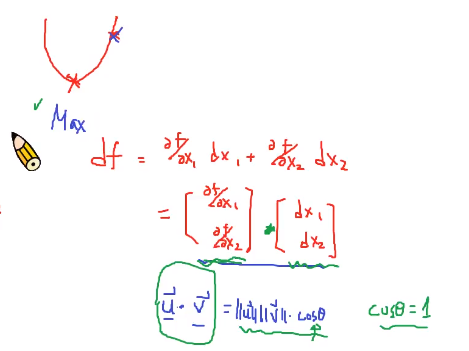
image.png

  • 两个向量共线时，df达到最值
  • 类比梯度下降与牛顿法求函数的“零点”

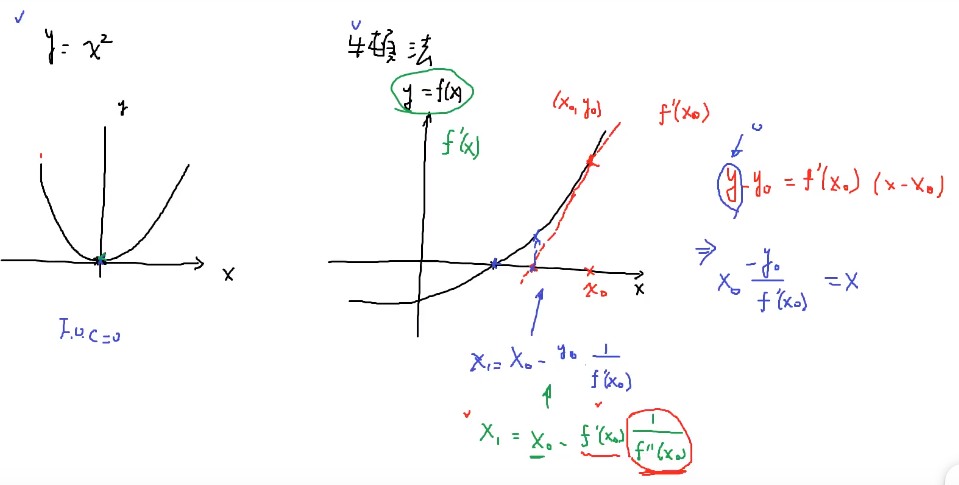
image.png

  • 以y=x^2为例，展示梯度下降寻找其极小点的过程

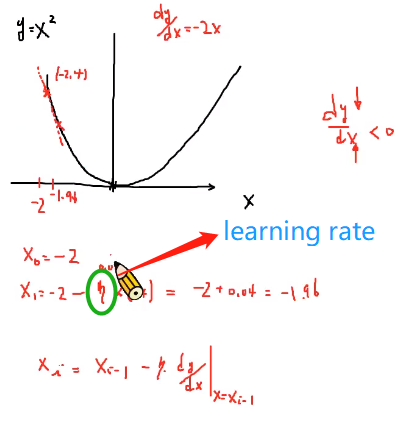
image.png

  • 当处于负半轴时，dy/dx<0,也就是说x增大y会减小(变化趋势相反)。
  • 我们想要找到极小值，就要使得y减小——>增大x、
  • 但是，负半轴时x都是负的—->减去一个负值
  • 正半轴类似的做法
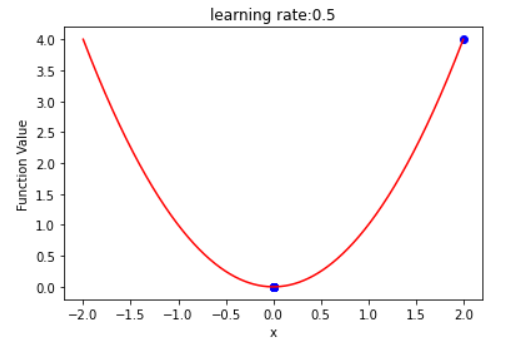
  • learning rate：取值要合适，取值过大可能会导致发散，不会逐渐收敛到极小值

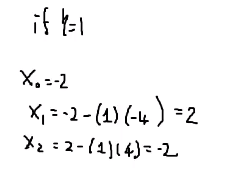image.png 以lr=1为例，会左右发散

  • 思考：单单以梯度为参考是否合适？
  • 简单的梯度下降往往会导致训练很长一段时间都不下降也不变化的情况，即找到了局部最小值

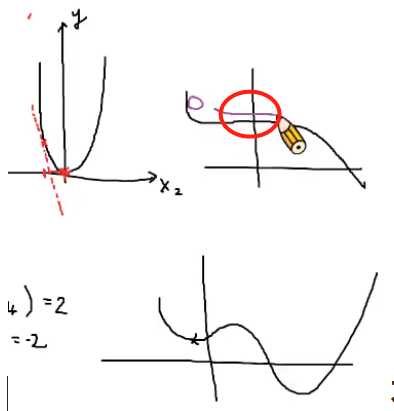
image.png

  • 不光要考虑梯度还要考虑动量，否则就有可能在平缓的地方一直左右摇摆，找不到真正的最小值

    3.两个比较常用的性能较好的优化器：Adam和RMSProp

    image.png

  • 详细介绍优化器的论文

  • Adam没有考虑动量只是对之前的所有梯度做了进一步处理
  • RMSProp考虑了动量，使其不会困于局部极小值或者平缓的地方

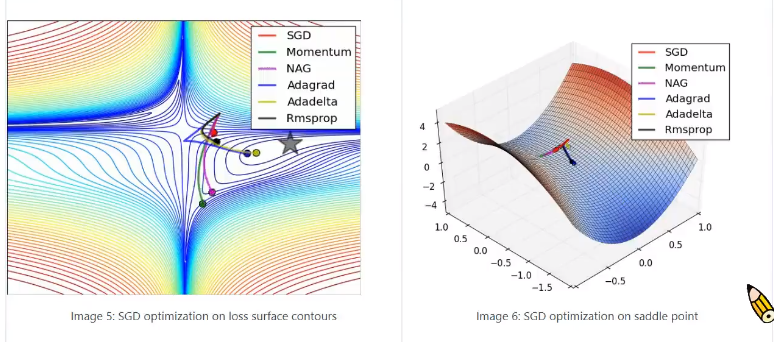
image.png

  • 论文里的图：用于比较各个优化器的优化过程

  • 动量：小球下落不只取决于斜坡陡不陡，还取决于能不能下降，有没有速度下降

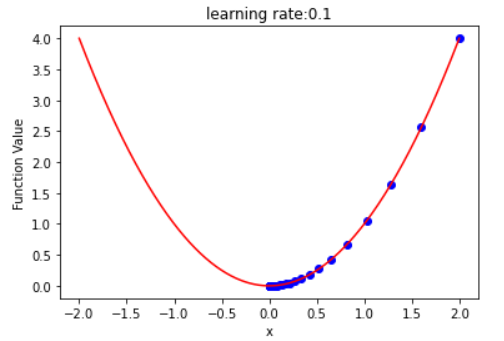
    4.以y=x^2为例，展示梯度下降的参数更新过程。

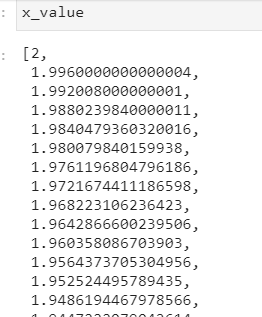    image.png image.png
    image.pngx从2开始，不断向0靠近

    1. y = np.max(np.abs(x_value))
    2. z = np.linspace(-y,y,num_iterate)
    3. plt.plot(x_value,fn_value,"bo")
    4. plt.plot(z,fn(z),"r")
    5. plt.xlabel('x')
    6. plt.ylabel('Function Value')
    7. plt.show()

  • 变量y表示x在梯度下降过程中绝对值最大值。[不能保证x都是朝希望的方向前进]

  • 绘图时横轴的范围即为：【-y,y】

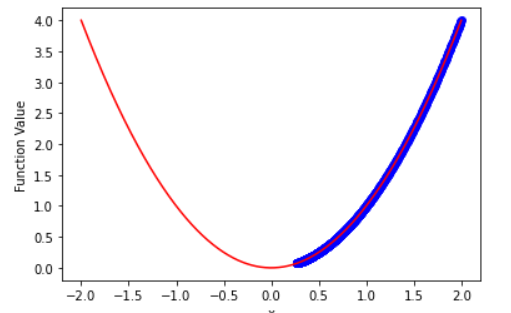
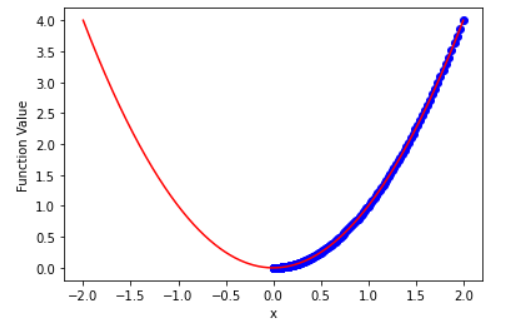
image.pngimage.png

  • 左图的学习率是0.001，可以发现在循环1000次后，还是没有到目标值0.
  • 右图的学习率是0.08，1000次后到达目标值.

image.png image.png