十二、神经网络与深度学习NN&DL

12.1 简介

• 我们之前学习的一系列分类和回归算法问题就在于，我们必须要知道判别函数的形式与样本的特征并对其进行优化

12.1.1 深度学习的定义与优点

• 深度学习(Deep Learning)是机器学习的一个分支。它是一系列由多个处理层组成的，用来学习高维度抽象数据和复杂结构的算法，由一系列非线性的transformation组成
• 传统的监督学习中，最重要的在于定义特征这一步骤，而深度学习实现了特征的主动提取，减少了对人工提取特征的需要

12.1.2 神经网络的历史

• 1957年的时候感知机Perceptron就已经被提出，这是一个简单的二层神经网络
  • 感知机只能学习一些线性可分的函数，对于复杂的函数无能为力
• 1969年，神经网络的第一次寒冬
  • 批学习和在线学习：一批一起学和一个个学的区别
  • 感知机存在一个误差边界
• 1970年代，Backpropagation被引入但是没有引起重视
• 1986年，Backpropagation被重新“发明”

12.1.3 神经网络的分类

• 多层前馈神经网络：
  • 输入层和输出层之间存在着多个隐层
  • 神经元之间不存在跨层的连接，也没有层内的连接，但是相邻的两层之间是全连接
• 神经网络具有万能近似性质，一个具有隐层的深度前馈网络并且拥有任何一种具有挤压性质的激活函数，那么只要给予网络足够数量的隐藏单元可以以人员已经都来拟合一个从有限维空间到另一个有限维空间的可测函数。
  • 常见的激活函数比如Sigmoid函数和ReLU都具有这样的作用
  • 万能近似定理告诉我们存在一个足够大的神经网络可以达到我们所希望的任意精度

12.2 逆向传播算法Back Propagation

12.2.1 简介

• 前向传播是指神经网络层接收输入数据并经过一系列隐藏单元进行层层计算，最终产生输出结果的过程，在传播的过程中，前向传播可以一直持续到产生一个标量代价函数，而反向传播允许代价函数的信息通过网络向后流动，以便计算梯度。

• 反向传播算法是目前最成功的神经网络的算法，不仅可以用在多层前馈神经网络中，也可以在别的神经网络中起作用

  • 反向传播只是一个用来计算梯度的算法
• 计算图：用有向图来表示一个神经网络的计算过程，节点表示中间变量，有向边表示计算的过程

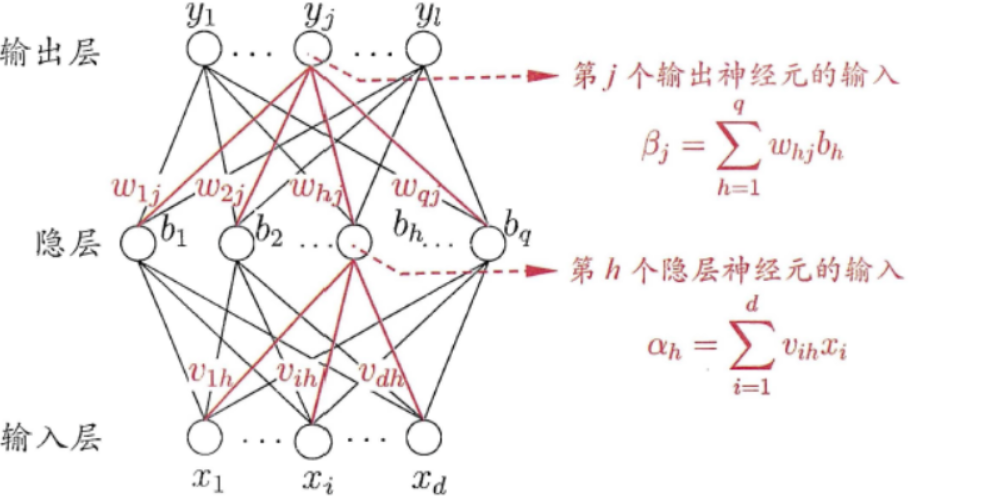
12.2.2 问题的定义和表示

• 给定训练集D，其中x由d个属性来表述，输出的结果y是l维的实向量，我们假设一个多层的前反馈网络如下所示：
• 该网络共有三层，分别是输入层、隐层、输出层
  • 输入层假设输入的样本有d个不同的特征，输出的结果有l个不同的特征
  • 隐层一共有q个和输入层全连接的神经元
  • 输入层的d个神经元到隐层q个神经元的权重是
  • 隐层q个神经元收到的输入是，阈值是，输出的结果是，连接到输出层的权重是
  • 输出层收到的输入是，阈值是，最终预测的结果是，结果的真实值是
  • 每一层都采用sigmoid函数作为激活函数

12.2.3 BP算法的具体内容

• 隐层接受的输入为：

• 隐层输出的结果是：

%0A#card=math&code=b_j%3Df%28%5Calpha_j-%5Cgamma_j%29%0A)

• 输出层接收到的输入是：

• 输入层输出的结果是：

%0A#card=math&code=z_k%3Df%28%5Cbeta_k-%5Ctheta_k%29%0A)

• 那么这一条样本的训练导致的均方误差是：

%5E2%0A#card=math&code=E%3D%5Cfrac%2012%5Csum_%7Bk%3D1%7D%5El%28z_k-y_k%29%5E2%0A)

• BP是一种迭代式的算法，采用梯度下降法进行训练，而我们待定的参数有：
  • %5Ctimes%20q#card=math&code=%28d%2Bl%29%5Ctimes%20q)个权值
  • 个层间输入和个层间输出
• 此外我们采用的sigmoid函数有非常好的性质，即：

%3Df(x)(1-f(x))%0A#card=math&code=f%27%28x%29%3Df%28x%29%281-f%28x%29%29%0A)

• 因此我们对均方误差进行求梯度，可以得到如下一些结果：

f’(%5Cbeta_k-%5Ctheta_k)%5C%5C%26%3D(z_k-y_k)f(%5Cbeta_k-%5Ctheta_k)(1-f(%5Cbeta_k-%5Ctheta_k))%5C%5C%26%3D(z_k-y_k)z_k(1-z_k)%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%5Cfrac%7B%5Cpartial%20E%7D%7B%5Cpartial%20%5Cbeta_k%7D%26%3D%5Cfrac%7B%5Cpartial%20E%7D%7B%5Cpartial%20z_k%7D%5Ctimes%20%5Cfrac%7B%5Cpartial%20z_k%7D%7B%5Cpartial%20%5Cbeta_k%7D%20%5C%5C%26%3D%28z_k-y_k%29f%27%28%5Cbeta_k-%5Ctheta_k%29%5C%5C%26%3D%28z_k-y_k%29f%28%5Cbeta_k-%5Ctheta_k%29%281-f%28%5Cbeta_k-%5Ctheta_k%29%29%5C%5C%26%3D%28z_k-y_k%29z_k%281-z_k%29%5Cend%7Baligned%7D%0A)

z_k(1-z_k)%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%5Cfrac%7B%5Cpartial%20E%7D%7B%5Cpartial%20%5Ctheta_k%7D%26%3D%5Cfrac%7B%5Cpartial%20E%7D%7B%5Cpartial%20z_k%7D%5Ctimes%20%5Cfrac%7B%5Cpartial%20z_k%7D%7B%5Cpartial%20%5Ctheta_k%7D%20%5C%5C%26%3D-%28z_k-y_k%29z_k%281-z_k%29%5Cend%7Baligned%7D%0A)

zk(1-z_k)%0A#card=math&code=%5Cfrac%7B%5Cpartial%20E%7D%7B%5Cpartial%20w%7Bjk%7D%7D%3Db_j%28z_k-y_k%29z_k%281-z_k%29%0A)

• 而神经网络的学习目标就是使得训练集D上的累计均方误差最小化：

• 因此在每一轮的训练中设定一定的学习率并不断进行迭代，就可以求解BP算法

12.3 卷积神经网络CNN

• 卷积神经网络CNN在2012年的ImageNet大赛中一战成名，但是在CNN大热之前已经有了一系列必要的条件

12.3.1 NN的重大突破

• ReLU作为激活函数的提出：
  • ReLU的中译名叫做线性整流单元

• ReLU的优点：
  • 对于一个特定的输入，一般的神经元处于silence状态
  • 相比于sigmoid函数，ReLU的表现性能更好并且对预训练不敏感
  • 更加节约计算资源
  • ReLU的函数梯度是固定的，只有0或者1，不会存在梯度不存在的点
  • 更适应于稀疏的特征
• Dropout算法
  • 每次迭代的过程中，每个神经元都有一定的几率被ignored
  • 即训练的时候每次随机将一部分的神经元激活，另一部分沉默，但是测试的时候让所有的神经元都处于激活状态

12.3.2 卷积Convolution

• 图像一般size都比较大，如果真的把整张图片作为输入，会使得参数个数出现指数级别的增长
• 但图像具有非常强的2D局部结构特征：相邻的一些像素点是有较强相关性的，因此可以利用这一点来压缩输入的数据
• 数学中的卷积是一种将两个函数进行积分的运算，产生的结果用来表示一个函数的形状是如何被另一个函数改变的：

(t)%3D%5Cint%20%5E%5Cinfty%7B-%5Cinfty%7Df(%5Cgamma)g(t-%5Cgamma)d%5Cgamma%0A#card=math&code=%28f%2Ag%29%28t%29%3D%5Cint%20%5E%5Cinfty%7B-%5Cinfty%7Df%28%5Cgamma%29g%28t-%5Cgamma%29d%5Cgamma%0A)

• 而在2D的图像中我们可以用如下方式计算卷积
  • 定义一个卷积核(2D数组，表示可以学习的参数)，大小是
  • 定义一个特征map，并用如下方式计算一张图片的卷积：

%5Bi%2Cj%5D%3D%5Csum%7Bm%3D-M%7D%5EM%5Csum%7Bn%3D-N%7D%5ENx%5Bi%2Bm%2Cj%2Bn%5Dw%5Bm%2Cn%5D%0A#card=math&code=s%5Cleft%5Bi%2Cj%5Cright%5D%3D%28x%2Aw%29%5Bi%2Cj%5D%3D%5Csum%7Bm%3D-M%7D%5EM%5Csum%7Bn%3D-N%7D%5ENx%5Bi%2Bm%2Cj%2Bn%5Dw%5Bm%2Cn%5D%0A)

• 不同的卷积核带来的效果

12.3.3 卷积层

• 卷积核(filter，也可以叫滤波器)需要覆盖输入图像的所有深度

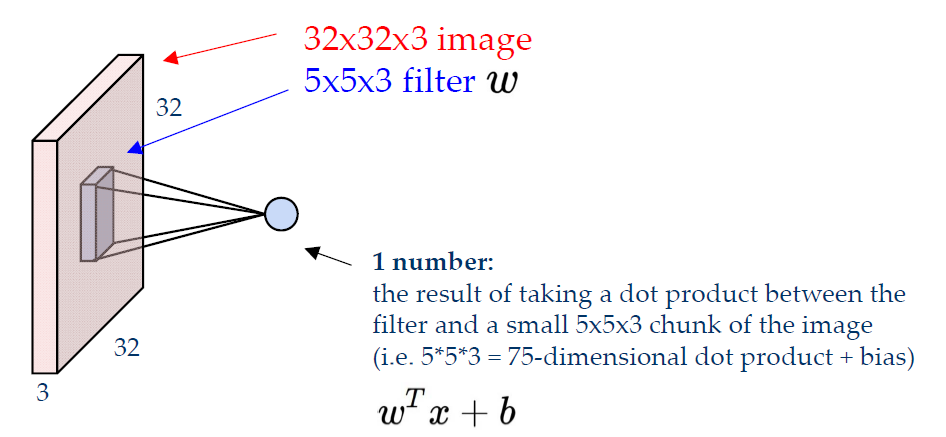
• 上图中32_32_3大小的输入图片在5_5_3的卷积核运算过后将留下28_28_1的activation maps，如果有多个大小相同的卷积核，那么就可以得到若干个不同的activation maps并将其组合成一张新的图片
  • 卷积网络由一系列的卷积层和穿插的激活函数组合而成

步长：卷积核的移动存在一个步长(stride)，卷积核移动的步长（stride）小于卷积核的边长时，变会出现卷积核与原始输入矩阵作用范围在区域上的重叠，卷积核移动的步长与卷积核的边长相一致时，不会出现重叠现象
接收域receptive field：卷积核可以覆盖到的局部特征区域，比如一个3_3的卷积核可以包含一个3_3区域内的信息，那么其接收域就是33，随着层数的加深，接受域也在变大。*大的步长也使得接受域的增大速度变快

• 靠近输入层的卷积层一般特征比较简单，靠近输出层的卷积层一般可以反映出更复杂的特征

12.3.4 池化层Pooling Layer

• 池化可以让特征的表示规模更小并且更加manageable，并且要在每个activation map中分别进行
• 平均池化average pooling
  • 按照池化窗口的大小计算该范围内的平均值，达到压缩图片大小的目的

• 最大值池化 Max-Pooling
  • 用一个window内的最大值来代替整个window中的值
• 池化层可以压缩卷积层得到的结果，并且可以控制过拟合

12.3.5 CNN的总体架构

• CNN的总体架构如下图所示：

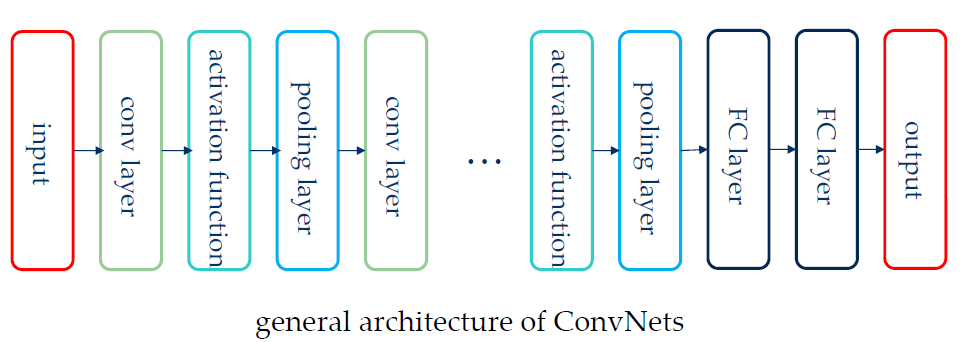
• 卷积网络的四个优点：
  • 局部连接
  • 共享权重
  • 池化pooling
  • 多个层级
• 图中的FC层是Full-Connection全连接层的意思
  • 有的神经网络没有FC层和池化层

12.4 CNN的实例

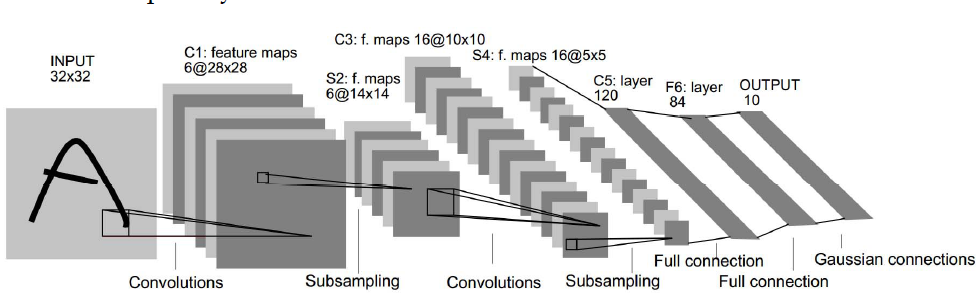
12.4.1 LeNet-5

• 这是CNN的第一个成功的应用，包括7个层
  • 卷积层用C表示，子采样层用S表示，全连接层用F表示

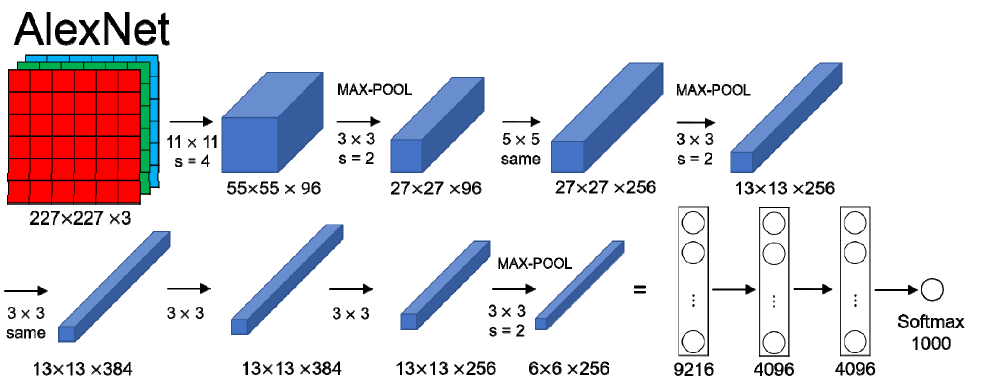
12.4.2 AlexNet

• 第一个在计算机视觉领域热门的网络，大约有60M个可训练的参数

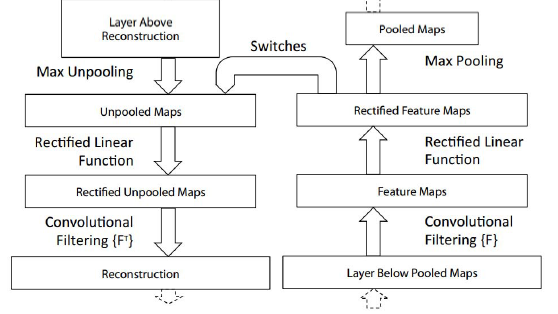
12.4.3 ZF Net

• 提出了一种将特征活动映射回输入像素空间的新方法

12.5 RNN与自然语言处理NLP

• 在自然语言处理中我们经常需要根据时间结构或者顺序结构来进行建模，比如视频的帧、音频的片段和句子的词语组成顺序

12.5.1 语言的建模

• 词语的预测实际上就是在给定了若干个词语的条件下预测下一个最有可能的词语的过程，可以用概率表达式表示成：

%0A#card=math&code=P%28x_%7Bt%2B1%7D%7Cx_t%2C%5Cdots%2Cx_1%29%0A)

• 为此，我们需要用时间或顺序结构以及不同长度的输入和输出对数据进行建模，为此我们可以使用RNN，即递归(循环)神经网络

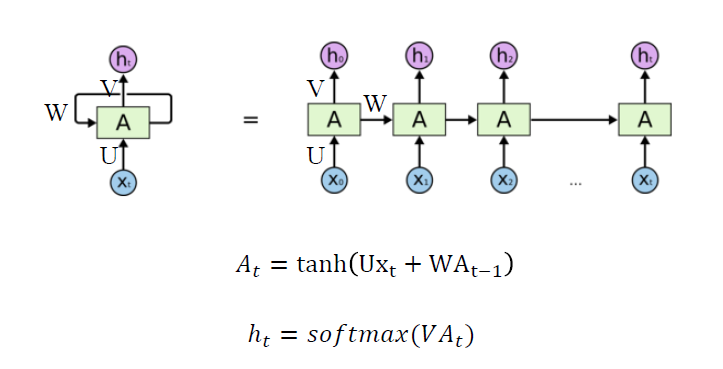
12.5.2 递归神经网络RNN简介

• RNN是一种联结模型(connectionist models)，可以有选择地跨序列传递信息，同时一次处理一个元素的顺序数据
  • RNN有一种允许存储先前的输入并保持网络的内部状态，并影响网络输出的机制

• RNN的输出层得到的结果是一个向量，但是我们需要将其转化成概率，此时就可以用到softmax激活函数，我们假设输出层输出的结果是一个向量#card=math&code=%28z_1%2C%5Cdots%2Cz_K%29)，那么softmax函数计算的每个输出对应的概率是：

12.5.3 RNN的优缺点

• RNN的一些优点：
  • 可以处理任意长度的输入，每次计算可以使用前几次计算中存储的信息
  • 模型的size不会随着输入的变长而增长
  • 每一步的权重相同，处理输入具有对城西
• RNN的缺点：
  • 计算速度慢，不能并行计算各个步骤
  • 从许多步骤中获取信息是比较困难的，这个问题也叫做 Vanishing Gradient Problem梯度消失问题

12.5.4 梯度消失问题Vanishing Gradient Problem

• BPTT训练法

• 看不懂 先不看了

12.5.5 LSTM

• 可以学习到long range dependency，LSTM在RNN的基础上增加了一个cell memory用来存储，一个普通的的LSTM单元由如下几部分组成：
  • cell state和hidden state
  • 三个控制门：Forget gate, input gate, output gate
  • 可以解决梯度消失问题

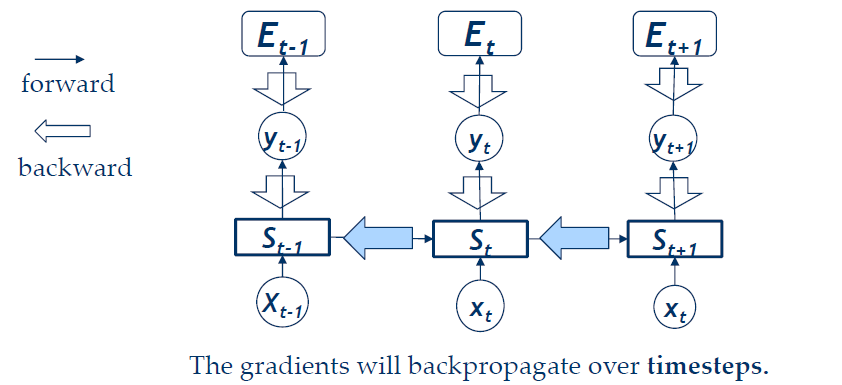
12.5.6 LSTM如何解决了VGP

• LSTM架构使得RNN可以更好地存储很多步之前的信息
  • 如果将forget门设置为1，将输入门设置为0，那么这个cell中的内容将永久保存
  • 并没有彻底消灭VGP，但是很大程度上解决了这个问题

12.5.7 RNN的输出

• 一对一：运行效果就跟MLP(多层感知机)是一样的
• 一对多：文章生成，给定一个随机数的种子，生成一篇文章
• 多对一：文本情绪分析和分类
• 多对多：
  • 输入输出长度不同：机器翻译
  • 长度相同：名称实体识别NER
• 经典的编码-解码RNN模型
  • 是一种多对多的模型

12.7 深度学习常用的Tricks

12.7.1 批归一化Batch Normalization

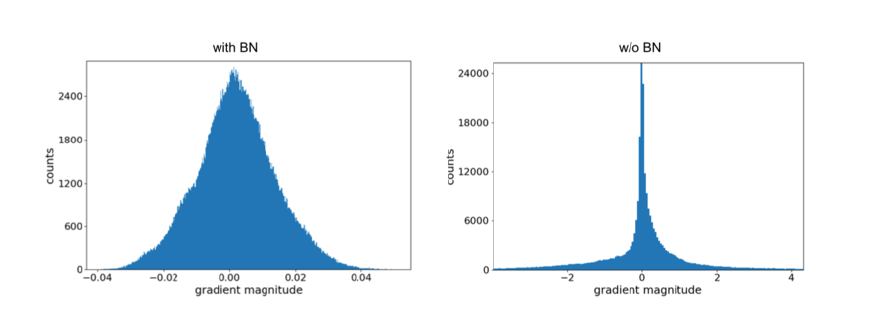
• 深度学习的网络训练中依然存在着梯度爆炸或者梯度消失的问题(即梯度太大或者太小)
• 批归一化处理是一种特殊的神经网络层用来将训练数据进行归一化的处理
  • 很多SOTA模型都用了这一trick
  • 因此常见的NN都具有如下的基本单元：卷积—批归一—ReLU函数

• 如果在网络的第K层输入的N个样本都记作%7D#card=math&code=x%5E%7B%28K%29%7D)，那么需要进行的归一化处理就是：

%7D%3D%5Cfrac%7Bx%5E%7B(K)%7D-E(x%5E%7B(K)%7D)%7D%7B%5Csqrt%7B%5Cmathrm%20%7Bvar%7D(x%5E%7B(K)%7D)%7D%7D%0A#card=math&code=%5Cbar%20x%5E%7B%28K%29%7D%3D%5Cfrac%7Bx%5E%7B%28K%29%7D-E%28x%5E%7B%28K%29%7D%29%7D%7B%5Csqrt%7B%5Cmathrm%20%7Bvar%7D%28x%5E%7B%28K%29%7D%29%7D%7D%0A)

• 在深度神经网络中，批归一化处理也可以正常使用，对于的情形，下面的归一化处理也可以使用：

%7D%7B%5Csqrt%7B%5Cmathrm%7Bvar%7D(y)%7D%7D%3D%5Cfrac%7Bwx%2Bb-E(wx%2Bb)%7D%7B%5Csqrt%20%7B%5Crm%7Bvar(wx%2Bb)%7D%7D%7D%0A#card=math&code=y%27%3D%5Cfrac%7By-E%28y%29%7D%7B%5Csqrt%7B%5Cmathrm%7Bvar%7D%28y%29%7D%7D%3D%5Cfrac%7Bwx%2Bb-E%28wx%2Bb%29%7D%7B%5Csqrt%20%7B%5Crm%7Bvar%28wx%2Bb%29%7D%7D%7D%0A)

• 发现经过上面的处理，即使w和b发生变化也不会影响批归一处理的结果

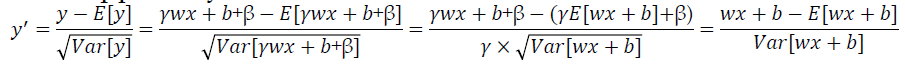
• 因此可以对批归一化层进行如下的参数学习：

%7D%3D%5Cgamma%5Ctimes%20%5Cfrac%7Bx%5E%7B(K)%7D-E(x%5E%7B(K)%7D)%7D%7B%5Csqrt%7B%5Cmathrm%20%7Bvar%7D(x%5E%7B(K)%7D)%7D%7D%2B%5Cbeta%0A#card=math&code=%5Cbar%20x%5E%7B%28K%29%7D%3D%5Cgamma%5Ctimes%20%5Cfrac%7Bx%5E%7B%28K%29%7D-E%28x%5E%7B%28K%29%7D%29%7D%7B%5Csqrt%7B%5Cmathrm%20%7Bvar%7D%28x%5E%7B%28K%29%7D%29%7D%7D%2B%5Cbeta%0A)

• 批归一化处理使得数据分布更加集中，避免了梯度的爆炸和消失

12.7.2 数据增加Data Augmentation

• 增加训练数据的量，避免出现过拟合的情况
• 对于同一张图片，可以通过图像的一些基本变换和处理产生更多的训练数据

12.7.3 神经网络的剪枝

• 一个神经网络所需要的资源可以分为存储资源和计算资源：
  • 存储资源是用于存储模型参数的资源
  • 计算资源是前传过程计算产生的cost
• 神经网络的剪枝的基本思想是删掉一些网络中不重要的组件，节约存储资源和计算资源
  • 关键在于如何衡量网络中各个组件的重要性
  • 主要的组件有权重、卷积时的滤波器、网络的层
  • Weight-level的剪枝主要有：
    • 将不重要的权重设置为0
    • 直接减少参数的个数
  • Filter‐level的剪枝主要有：
    • 去掉不重要的filter
    • 直接减少参数或者计算的规模
  • Layer-Level的剪枝主要是直接删除不重要的层
• 几种剪枝的缺点
  • Weight-level pruning使得权重矩阵变得稀疏，但是移动设备上的库函数对稀疏矩阵的支持比较有限
  • Filter-level pruning：如何定义不重要的filter？众说纷纭，可以根据范数的大小、特征图的mean activation values、filter的重复性等来评判
  • Layer-level pruning

12.8 生成对抗网络GAN

• GAN可以通过学习生成一些图像。比如人脸、风景、画作等等