📅 第三轮刷题

字符串匹配

public int search(String txt, String pat) {
    int i, N = txt.length();
    int j, M = pat.length();
    for (int i = 0, j = 0; i < N && j < M; i++) {
        if (txt.charAt(i) == pat.charAt(j)) {
            j++;
        } else {
            i -= j;
            j = 0;
        }
    }
    if (j == M) return i - M;
    else return N;
}

📌 第一周 1ST

剑指 Offer 03. 数组中重复的数字

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，请找出数组中任意一个重复的数字。

class Solution {
    public int findRepeatNumber(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == i) {
                continue;
            } else if (nums[nums[i]] == nums[i]) {
                return nums[i];
            } else {
                swap(nums,nums[i], i);
            }
        }
        return -1;
    }
    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

剑指 Offer 07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return traverse(preorder, 0, preorder.length - 1,
                        inorder, 0, inorder.length - 1);
    }
    private TreeNode traverse(int[] preorder, int preS, int preE,
                          int[] inorder, int inS, int inE) {
        if (preS > preE) return null;//一开始边界条件没有加，注意
        int rootVal = preorder[preS];
        int index = 0;
        for (int i = inS; i <= inE; i++) {
            if (inorder[i] == rootVal) {
                index = i;
                break;
            }
        }
        TreeNode root = new TreeNode(rootVal);
        int leftval = index - inS;
        root.left = traverse(preorder, preS + 1, preS + leftval,
                             inorder, inS, index - 1);
        root.right = traverse(preorder,preS + leftval + 1, preE,
                              inorder, index + 1, inE);
        return root;
    }
}

剑指 Offer 09. 用两个栈实现队列

class CQueue {
    Stack<Integer> in; 
    Stack<Integer> out; 
    public CQueue() {
        in = new Stack<>();
        out = new Stack<>();
    }
    public void appendTail(int value) {
        in.push(value);
    }
    public int deleteHead() {
        if (out.isEmpty()) {
            //while保证in里面的全部元素都压进out里面
            while (!in.isEmpty()) {
                out.push(in.pop());
            }
        }
        if (out.isEmpty())
            return -1;
        return out.pop();
    }
}

剑指 Offer 10- I. 斐波那契数列

class Solution {
    public int fib(int n) {
        if(n == 0) return 0;
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            dp[i] = dp[i-1] + dp[i-2];
            dp[i] %= 1000000007;
        }
        return dp[n];
    }
}

剑指 Offer 11. 旋转数组的最小数字

输入：[3,4,5,1,2]
输出：1

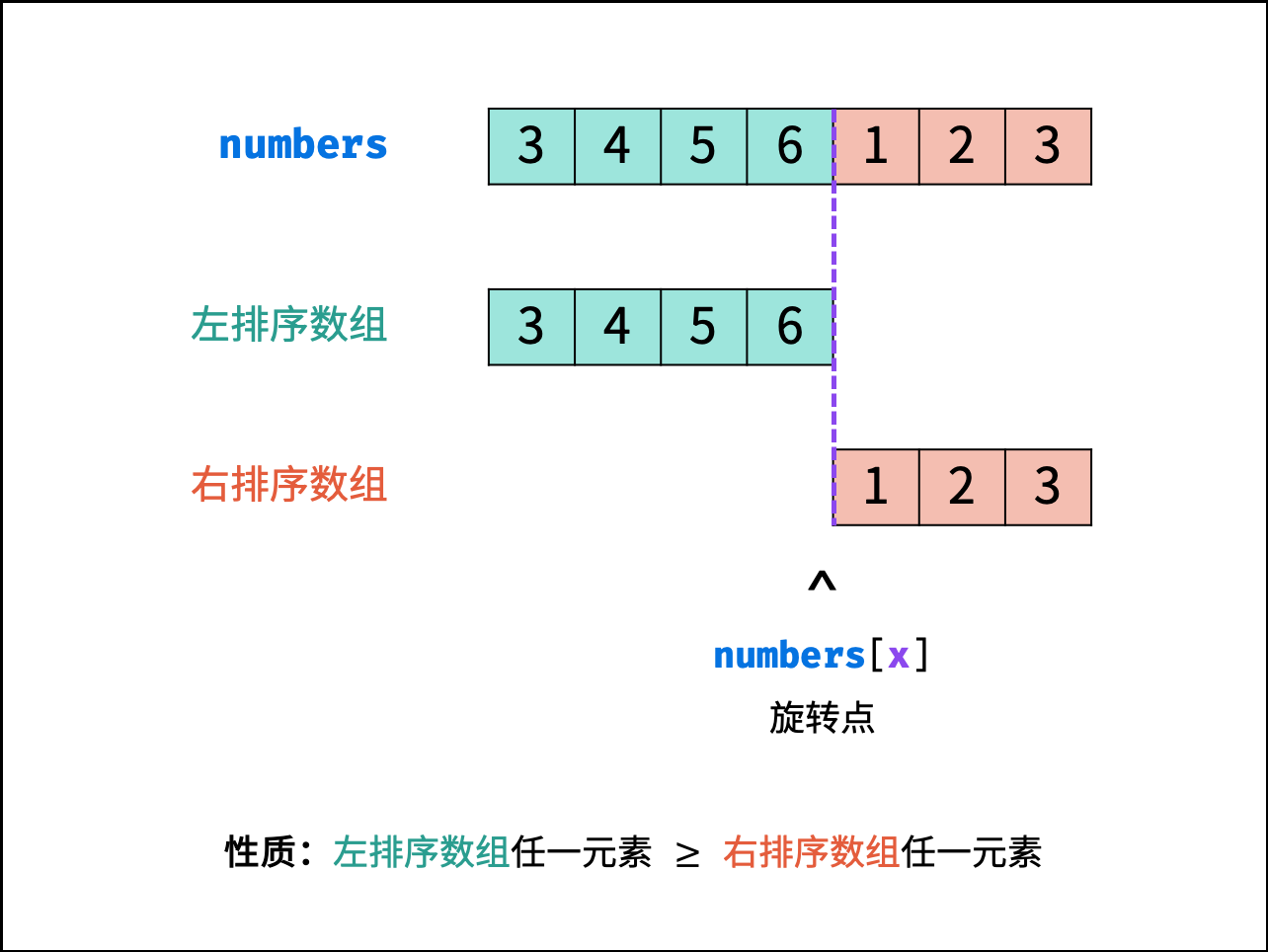
class Solution {
    public int minArray(int[] numbers) {
        int i = 0, j = numbers.length - 1;
        while (i < j) {
            int m = (i + j) / 2;
            if (numbers[m] < numbers[j]) j = m;
            else if (numbers[m] > numbers[j]) i = m + 1;
            else j--;//无法确定左区间还是右区间，缩小j
        }
        return numbers[j];
    }
}

剑指 Offer 12. 搜索单词

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

class Solution {
    private int[][] direction = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
    private int m;
    private int n;
    public boolean exist(char[][] board, String word) {
        if (word == null || word.length() == 0) return true;
        if (board == null || board.length == 0) return false;
        m = board.length;
        n = board[0].length;
        boolean[][] hasVisited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (backtrack(board, word, hasVisited,i, j, 0)) return true;
            }
        }
        return false;
    }
    private boolean backtrack(char[][] board, String word, boolean[][] visited, int r, int c, int k) {
        if (k == word.length()) {
            return true;
        }
        if (r < 0 || r >= m || c < 0 || c >= n
            || board[r][c] != word.charAt(k) || visited[r][c]) {
            return false;
        }
        visited[r][c] = true;
        for (int[] d : direction) {
            int dr = r + d[0];
            int dc = c + d[1];
            if (backtrack(board, word, visited, dr, dc, k + 1)) return true;
        }
        visited[r][c] = false;
        return false;
    }
}

剑指 Offer 15. 二进制中1的个数

//把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0.
//那么一个整数的二进制有多少个1，就可以进行多少次这样的操作。
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count=0;
        while(n!=0){
            count++;
            n=n&(n-1);
        }
        return count;
    }
}

剑指 Offer 16. 数值的整数次方

输入：x = 2.00000, n = 10
输出：1024.00000

class Solution {
    public double myPow(double x, int n) {
        double res = 1.0;
        for(int i = n; i != 0; i /= 2) {
            if(i % 2 != 0){
                res *= x;
            }
            x *= x;
        }
        return  n < 0 ? 1 / res : res;
    }
}

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

输入：nums = [1,2,3,4]
输出：[1,3,2,4]

class Solution {
    //while循环里面三个判断都没有加i < j
    public int[] exchange(int[] nums) {
        int i = 0, j = nums.length - 1;
        while (i < j) {
            while (i < j && nums[i] % 2 != 0)
                i++;
            while (i < j && nums[j] % 2 == 0)
                j--;
            if (i < j) {
                int t = nums[i];
                nums[i] = nums[j];
                nums[j] = t;
            }
        }
        return nums;
    }
}

剑指 Offer 29. 顺时针打印矩阵

class Solution {
    public int[] spiralOrder(int[][] matrix) {
        if (matrix.length == 0) return new int[0];
        int l = 0;
        int r = matrix[0].length - 1;
        int t = 0;
        int b = matrix.length - 1;
        int x = 0;
        int[] res = new int[(r + 1) * (b + 1)];
        while (true) {
            //从左往右
            //列在变，列为循环值
            //从左往右的下一步是往下走，上边界内缩，故++t
            //每做完一次循环收缩边界
            for (int i = l; i <= r; i++) res[x++] = matrix[t][i];
            if (++t > b) break;
            for (int i = t; i <= b; i++) res[x++] = matrix[i][r];
            if (--r < l) break;
            for (int i = r; i >= l; i--) res[x++] = matrix[b][i];
            if (--b < t) break;
            for (int i = b; i >= t; i--) res[x++] = matrix[i][l];
            if (++l > r) break;
        }
        return res;
    }
}

剑指 Offer 30. 包含min函数的栈

class MinStack {
    /** initialize your data structure here. */
    Stack<Integer> A, B;
    public MinStack() {
        A = new Stack<>();
        B = new Stack<>();
    }
    public void push(int x) {
        A.push(x);
        if (B.isEmpty() || B.peek() >= x) {
            B.push(x);
        }
    }
    public void pop() {
        if (A.pop().equals(B.peek()))
            B.pop();
    }
    public int top() {
        return A.peek();
    }
    public int min() {
        return B.peek();
    }
}

剑指 Offer 33. 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        return recur(postorder, 0, postorder.length - 1);
    }
    private boolean recur(int[] nums, int s, int e) {
        if (s >= e) return true;
        int rootVal = nums[e];
        int m = s;
        while(m < e && nums[m] < rootVal) {
            m++;
        }
        int k = m;
        while (k < e && nums[k] > rootVal) {
            k++;
        }
        return k == e && recur(nums, s, m - 1) && recur(nums, m, e - 1);
    }
}

剑指 Offer 34. 二叉树中和为某一值的路径

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1
输出：
[
   [5,4,11,2],
   [5,8,4,5]
]

class Solution {
    List<List<Integer>> ret = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        if (root == null) return ret;
        List<Integer> track = new ArrayList<>();
        backtrack(track, root, target);
        return ret;
    }
    private void backtrack(List<Integer> track, TreeNode root, int target) {
        if (root == null) return;
        track.add(root.val);
        if (root.left == null && root.right == null && target == root.val) {
            ret.add(new ArrayList<>(track));
            //return;//不能加return，返回上一层状态没有重置
        }
        backtrack(track, root.left, target - root.val);
        backtrack(track, root.right, target - root.val);
        track.remove(track.size() - 1);
    }
}

剑指 Offer 35. 复杂链表的复制

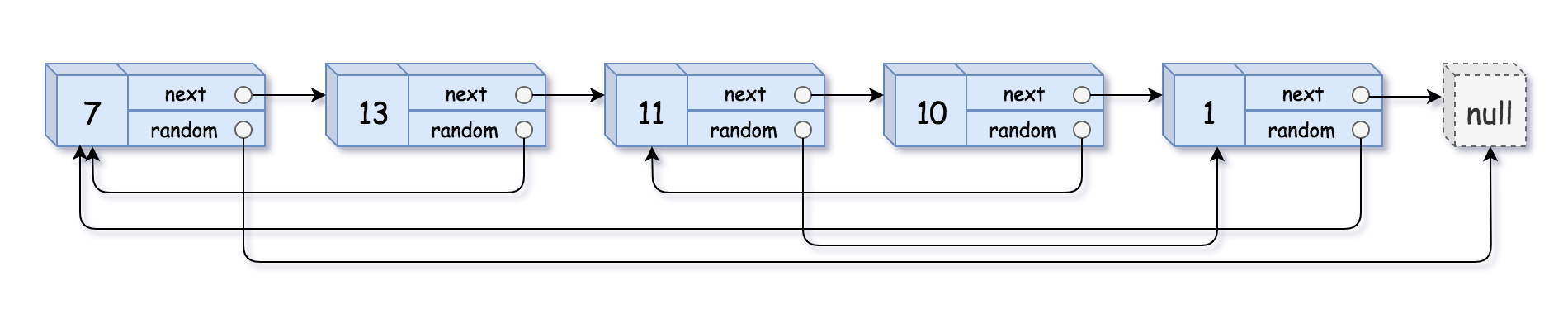
class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) return null;
        // 1. 复制各节点，并构建拼接链表
        Node cur = head;
        while (cur != null) {
            Node next = cur.next;
            Node temp = new Node(cur.val);
            cur.next = temp;
            temp.next = next;
            cur = next;
        }
        //2.复制random
        cur = head;
        while (cur != null) {
            if (cur.random != null)
                cur.next.random = cur.random.next;
            cur = cur.next.next;
        }
        // 3. 拆分两链表
        cur = head.next;
        Node pre = head, res = head.next;
        while(cur.next != null) {
            pre.next = pre.next.next;
            cur.next = cur.next.next;
            pre = pre.next;
            cur = cur.next;
        }
        pre.next = null; // 单独处理原链表尾节点
        return res;      // 返回新链表头节点
    }
}
/**
1.链表问题有时需要cur = head;
2.在第二步复制random的时候没有判断cur.random是否为空
3.拆分的时候要注意有一个pre节点，把最后指向复制链表的地方断开！
*/

剑指 Offer 36. 二叉搜索树与双向链表

class Solution {
    Node head, pre;
    public Node treeToDoublyList(Node root) {
        if (root == null) return null;
        dfs(root);
        //首尾节点互指
        pre.right = head;
        head.left = pre;
        return head;
    }
    private void dfs(Node cur) {
        if (cur == null) return;
        dfs(cur.left);
        if (head == null) 
            head = cur;
        if (pre != null)
            pre.right = cur;
            cur.left = pre;
        pre = cur;
        dfs(cur.right);
    }
}

剑指 Offer 39. 数组中出现次数超过一半的数字

//时间O(n)，空间O(1)
class Solution {
    public int majorityElement(int[] nums) {
        int x = 0, vote = 0;//x为众数，vote为票数
        for (int num : nums) {
            if (vote == 0) x = num;
            vote += num == x ? 1 : -1;
        }
        return x;
    }
}

需要的数字出现次数多于一半 那么排序后必定在中间

//时间O(nlogn)，空间O(1)
class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length/2];
    }
}

剑指 Offer 41. 数据流中的中位数

核心思想：大顶堆存放较小的元素，小顶堆存放较大的元素！！！

class MedianFinder {
    PriorityQueue<Integer> small;
    PriorityQueue<Integer> large;
    public MedianFinder() {
        small = new PriorityQueue<>((v1, v2) -> v2 - v1);//大堆顶
        large = new PriorityQueue<>();//小堆顶
    }
    //维持两个顶堆的元素不超过1
    public void addNum(int num) {
        if (small.size() < large.size()) {
            large.offer(num);
            small.offer(large.poll());
        } else {
            small.offer(num);
            large.offer(small.poll());
        }
    }
    public double findMedian() {
        if (large.size() > small.size()) {
            return large.peek();
        } else if (large.size() < small.size()) {
            return small.peek();
        } 
        return (large.peek() + small.peek()) / 2.0;
    }
}

剑指 Offer 43. 1～n 整数中 1 出现的次数

class Solution {
    public int countDigitOne(int n) {
        return f(n);
    }
    //下面我们都用 1234 和 2345 来举例
    private int f(int n){
        // 上一级递归 n = 20、10之类的整十整百之类的情况；以及n=0的情况
        if(n== 0) return 0;
        // n < 10 即为个位，这样子只有一个1
        if(n < 10) return 1;
        String s = String.valueOf(n);
        //长度：按例子来说是4位
        int length = s.length();
        //这个base是解题速度100%的关键，本例中的是999中1的个数：300
        // 99的话就是20 ; 9的话就是1 ；9999就是4000 这里大家应该发现规律了吧。
        int base = (length-1)*(int)Math.pow(10,length-2);
        //high就是最高位的数字
        int high = s.charAt(0) - '0';
        //cur就是当前所数量级，即1000
        int cur = (int)Math.pow(10,length -1);
        if(high == 1){
            //最高位为1，1+n-cur就是1000~1234中由千位数提供的1的个数，剩下的f函数就是求1000~1234中由234产生的1的个数
            return base + 1 + n - cur + f(n - high * cur); 
        }else{
            //这个自己思考
            return base * high + cur + f(n- high * cur);
        }
    }
}

剑指 Offer 44. 数字序列中某一位的数字

class Solution {
    public int findNthDigit(int n) {
        int digit = 1;// 记录位数，初始为一位数
        long start = 1; // 记录某一位数起始的第一个数，初始为一位数起点1
        long count = 9;// 记录某一位数所有包含的数字个数，初始为一位数个数9
        while (n > count) { 
            n -= count;
            digit += 1;
            start *= 10;
            count = digit * start * 9;
        }
        long num = start + (n - 1) / digit; // 2.判断第n位数字属于哪一个数
        return Long.toString(num).charAt((n - 1) % digit) - '0'; // 3.对位数取余得到哪一位
    }
}

剑指 Offer 45. 把数组排成最小的数

输入: [3,30,34,5,9]
输出: "3033459"

class Solution {
    public String minNumber(int[] nums) {
        if (nums == null || nums.length == 0) return "";
        int n = nums.length;
        String[] arr = new String[n];
        for (int i = 0; i < n; i++)
            arr[i] = nums[i] + "";
        Arrays.sort(arr, (s1, s2) -> (s1 + s2).compareTo(s2 + s1));
        String ret = "";
        for (String str : arr)
            ret += str;
        return ret;
    }
}

剑指 Offer 46. 把数字翻译成字符串

输入: 12258
输出: 5
解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

class Solution {
    public int translateNum(int num) {
        String s = String.valueOf(num);
        int[] dp = new int[s.length() + 1];
        dp[0] = dp[1] = 1;
        for (int i = 2; i <= s.length(); i++) {
            String tmpStr = s.substring(i - 2, i);
            if (tmpStr.compareTo("10") >= 0 && tmpStr.compareTo("25") <= 0) {
                dp[i] = dp[i - 1] + dp[i - 2];
            } else {
                dp[i] = dp[i - 1];
            }
        }
        return dp[s.length()];
    }
}
//理解dp数组的含义
//dp[i]就是第i个字符有多少种翻译的方法
//[i-1..i]如果可以组成一种方法，该情况就为dp[i-2]的大小
//[i]组成一种翻译方法，该情况就为dp[i-1]的大小

剑指 Offer 49. 丑数

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

class Solution {
    //dp[i]表示第i+1个丑数
    //这个题用三指针，第一个丑数是1，以后的丑数都是基于前面的小丑数分别乘2，3，5构成的。
    //我们每次添加进去一个当前计算出来个三个丑数的最小的一个，并且是谁计算的，谁指针就后移一位。
    public int nthUglyNumber(int n) {
        if (n <= 0)
            return -1;
        int[] dp = new int[n];
        dp[0] = 1;
        int id2 = 0, id3 = 0, id5 = 0;
        for (int i = 1; i < n; i++) {
            dp[i] = Math.min(dp[id2] * 2, Math.min(dp[id3] *3, dp[id5] * 5));
            // 这里不用else if的原因是有可能id2(3) * 2 == id3(2) * 3
            // 这种情况两个指针都要后移
            if (dp[id2] * 2 == dp[i])
                id2 += 1;
            if (dp[id3] * 3 == dp[i])
                id3 += 1;
            if (dp[id5] * 5 == dp[i])
                id5 += 1; 
        }
        return dp[n - 1];
    }
}

剑指 Offer 51. 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
归并排序

输入: [7,5,6,4]
输出: 5

class Solution {
    //用来统计逆序对的个数
    int count = 0;
    public int reversePairs(int[] nums) {
        merge(nums, 0, nums.length - 1);
        return count;
    }
    public void merge(int[] nums, int left, int right) {
        int mid = (left + right) / 2;
        if (left < right) {
            merge(nums, left, mid);
            merge(nums, mid + 1, right);
            mergeSort(nums, left, mid, right);
        }
    }
    public void mergeSort(int[] nums, int left, int mid, int right) {
        int[] temparr = new int[right - left + 1];
        int index = 0;
        int temp1 = left, temp2 = mid + 1;//左右两部分的起始索引
        while (temp1 <= mid && temp2 <= right) {
            if (nums[temp1] <= nums[temp2]) {
                temparr[index++] = nums[temp1++];
            } else {
                count += (mid - temp1 + 1);//左边和右边是有序的，当temp1>temp2时
                //说明temp1到mid的值都比temp2大，一共有这么多逆序对
                temparr[index++] = nums[temp2++];
            }
        }
        //把左边剩余的数移入数组
        while (temp1 <= mid) {
            temparr[index++] = nums[temp1++];
        }
        //把右边剩余的数移入数组
        while (temp2 <= right) {
            temparr[index++] = nums[temp2++];
        }
        //把新数组中的数覆盖nums数组
        //没有理解
        for (int k = 0; k < temparr.length; k++) {
            nums[k + left] = temparr[k];
        }
    }
}

剑指 Offer 53 - II. 0～n-1中缺失的数字

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

输入: [0,1,3]
输出: 2

class Solution {
    //缺失的数字等于 “右子数组的首位元素” 对应的索引；因此考虑使用二分法查找 “右子数组的首位元素”
    public int missingNumber(int[] nums) {
        int i = 0, j = nums.length - 1;
        while (i <= j) {
            int m = (i + j) / 2;
            if (nums[m] == m) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}

41. 缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

输入：nums = [3,4,-1,1]
输出：2

class Solution {
    public int firstMissingPositive(int[] nums) {
        int len = nums.length;
        for (int i = 0; i < len; i++) {
            while (nums[i] > 0 && nums[i] <= len && nums[nums[i] - 1] != nums[i]) {
                swap(nums, nums[i] - 1, i);
            }
        }
        for (int i = 0; i < len; i++) {
            if (nums[i] != i + 1)
                return i + 1;
        }
        return len + 1;
    }
    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

剑指 Offer 56 - I. 数组中数字出现的次数

由于数组中存在着两个数字不重复的情况，我们将所有的数字异或操作起来，最终得到的结果是这两个数字的异或结果

class Solution {
    public int[] singleNumbers(int[] nums) {
        //用于将所有的数异或起来
        int k = 0;
        // e.g. [2,4,2,3,3,6] 异或和：(2^2)^(3^3)^(4^6)=2=010
        for(int num: nums) {
            k ^= num;
        }
        //获得k中最低位的1
        int mask = 1;
         & operator只有1&1时等于1 其余等于0
        // 用上面的e.g. 4和6的二进制是不同的 我们从右到左找到第一个不同的位就可以分组 4=0100 6=0110
        // 根据e.g. 010 & 001 = 000 = 0则 mask=010
        // 010 & 010 != 0 所以mask=010
        // 之后就可以用mask来将数组里的两个数分区分开
        while((k & mask) == 0) {
            mask <<= 1;
        }
        int a = 0;
        int b = 0;
        for(int num: nums) {
            //根据&是否为0区分将两个数字分区，并分别求异或和
            if((num & mask) == 0) {
                a ^= num;
            } else {
                b ^= num;
            }
        }
        return new int[]{a, b};
    }
}

剑指 Offer 57 - II. 和为s的连续正数序列

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

输入：target = 9
输出：[[2,3,4],[4,5]]

class Solution {
    public int[][] findContinuousSequence(int target) {
        List<int[]> list = new ArrayList<>();
        //套滑动窗口模板，l是窗口左边界，r是窗口右边界，窗口中的值一定是连续值。
        //当窗口中数字和小于target时，r右移; 大于target时，l右移; 等于target时就获得了一个解
        for (int l = 1, r = 1, sum = 0; r < target; r++) {
            sum += r;
            while (sum > target) {
                sum  -= l;
                l++;
            }
            if (sum == target) {
                int[] temp = new int[r - l + 1];
                for (int i = 0; i < temp.length; i++) {
                    temp[i] = l + i;
                }
                list.add(temp);
            }
        }
        int[][] res = new int[list.size()][];
        for (int i = 0; i < res.length; i++) {
            res[i] = list.get(i);
        }
        return res;
    }
}

剑指 Offer 58 - I. 翻转单词顺序

Input:
"I am a student."
Output:
"student. a am I"

public String ReverseSentence(String str) {
    int n = str.length();
    char[] chars = str.toCharArray();
    int i = 0, j = 0;
    while (j <= n) {
        if (j == n || chars[j] == ' ') {
            reverse(chars, i, j - 1);
            i = j + 1;
        }
        j++;
    }
    reverse(chars, 0, n - 1);
    return new String(chars);
}
private void reverse(char[] c, int i, int j) {
    while (i < j)
        swap(c, i++, j--);
}
private void swap(char[] c, int i, int j) {
    char t = c[i];
    c[i] = c[j];
    c[j] = t;
}

剑指 Offer 59 - I. 滑动窗口的最大值

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 
  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 0 || k == 0) return new int[0];
        int n = nums.length;
        // 双向队列 保存当前窗口最大值的数组位置 保证队列中数组位置的数按从大到小排序
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[n - k + 1];
        for (int i = 0; i < n; i++) {
            // 保证从大到小 如果前面数小 弹出
            while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
                deque.pollLast();
            }
            deque.offerLast(i);
            //等到窗口长度为k时 下次移动在删除过期数值
            if (deque.peekFirst() <= i - k) {
                deque.pollFirst();
            }
            if (i - k + 1 >= 0) {
                res[i - k + 1] = nums[deque.peekFirst()];
            }
        }
        return res;
    }
}

60. 十进制转换八进制

public static void main(String[] args) {
    Scanner number=new Scanner(System.in);
    int n=number.nextInt();
    String result="";
    while (n>8) {
        result = n%8+result;
        n=n/8;
    }
    result = n+result;
    System.out.println(result);
}

📌 第二周 Leetcode

621. 任务调度器

你需要计算完成所有任务所需要的 最短时间 。

输入：tasks = ["A","A","A","B","B","B"], n = 2输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，
而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。

class Solution {
    //填桶
    public int leastInterval(char[] tasks, int n) {
        int[] temp = new int[26];
        int countMaxTask = 0;
        int maxTask=0;
        for(char c:tasks){
            temp[c-'A']++;
            maxTask = Math.max(temp[c-'A'],maxTask);
        }
        for(int i=0;i<26;i++){
            if(temp[i]==maxTask){
                countMaxTask++;
            }
        }
        return Math.max(tasks.length,(maxTask-1)*(n+1)+countMaxTask);
        //总排队时间 = (桶个数 - 1) * (n + 1) + 最后一桶的任务数
    }
}