Laten Factor Model 隐因子模型

算法思想

协同过滤的思路就是基于用户和物品的交互行为，要么计算用户间的相似度，推荐相似度高的用户喜欢的物品，因为这两个用户可能兴趣相投；要么就是计算物品间的相似度，推荐和历史记录相似度很高的物品，因为他们可能属于同一类别的商品。
我们做决策的基础都是默认了物品是有类别的，可能有的用户都喜欢某一类物品，所以这些用户之间相似度高，可能有的物品是属于同一类别的，因此这些物品的相似度很高。那既然这样，有没有可能直接得到物品的类别呢？这样我们就可以直接根据类别去进行推荐了。LFM就是基于这样的想法，假设物品存在若干个属性，那么每个用户对每个属性会有一个兴趣度，同样的，物品在每个属性上又都存在着一个权重。计算用户对物品的喜爱程度，就可以使用用户对物品属性的喜爱程度与物品的属性乘积。
该算法的核心思想是转化成一个矩阵分解问题，然后用传统机器学习算法去优化分解得到的矩阵。

举例介绍

我们用表示用户，表示物品，表示用户i对于物品j的评分，也就是喜好度。那么我们需要得到一个关于用户-物品的二维矩阵，如下面的矩阵：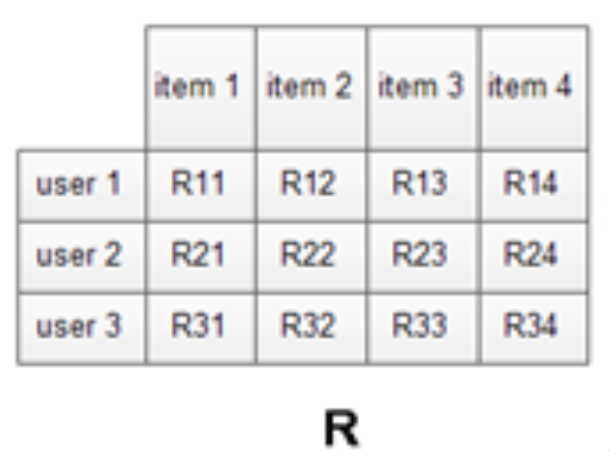

常见的系统中， 是一个非常稀疏的矩阵，因为我们不可能得到所有用户对于所有物品的评分。于是利用稀疏的，填充得到一个满矩阵就是我们的目的。

下面我们就来看看LFM是如何解决上面的问题的？对于一个给定的用户行为数据集（数据集包含的是所有的user, 所有的item，以及每个user有过行为的item列表），使用LFM对其建模后，我们可以得到如下图所示的模型：（假设数据集中有3个user, 4个item, LFM建模的分类数为4）: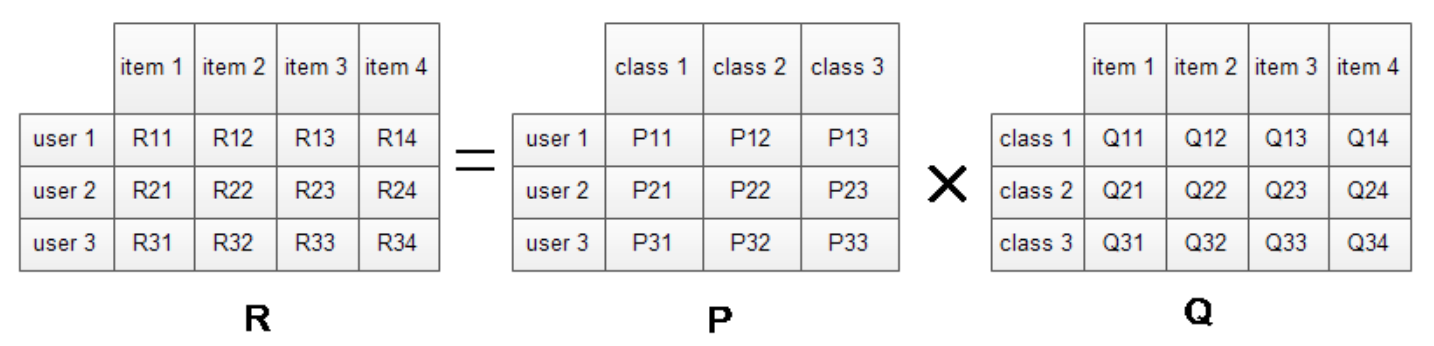

矩阵是user-item矩阵，矩阵值表示的是user i对item j的兴趣度，这正是我们要求的值。对于一个user来说，当计算出他对所有item的兴趣度后，就可以进行排序并作出推荐。LFM算法从数据集中抽取出若干主题，作为user和item之间连接的桥梁，将 矩阵表示为 矩阵和 矩阵相乘。其中 矩阵是user-class矩阵，矩阵值 表示的是user i对class j的兴趣度；矩阵式class-item矩阵，矩阵值表示的是item j在class i中的权重，权重越高越能作为该类的代表。所以LFM根据如下公式来计算用户 对物品 的兴趣度：


其中 K 为隐因子的个数。