SVD与推荐系统

首先了解一下SVD的原理

本部分主要引用文章 https://www.cnblogs.com/pinard/p/6251584.html 做部分修改

回顾特征值和特征向量

下特征值和特征向量的定义如下：

其中A是一个 的实对称矩阵， 是一个 维向量，则我们说 是矩阵A的一个特征值，而 是矩阵A的特征值 所对应的特征向量。
求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的𝑛个特征值，以及这 个特征值所对应的特征向量 , 如果这 个特征向量线性无关，则矩阵A可用如下的特征值分解：

其中, 是这 个特征向量所张成的 维矩阵，而 为这 个特征值为主对角线的 维矩阵。
一般我们会把 的这 个特征向量标准化，即满足 , 或者说 ，此时 的 个特征向量为标准正交基，满足 ，即 , 也就是说 为酉矩阵。
这样我们的特征分解表达式可以写成：

注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

SVD的定义

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个 的矩阵，那么我们定义矩阵A的SVD为：

其中 是一个 的矩阵， 是一个 的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值， 是一个 的矩阵。 和 都是酉矩阵，即满足 , 。下图可以很形象的看出上面SVD的定义：

那么我们如何求出SVD分解后的 这三个矩阵呢？

如果我们将 的转置和 做矩阵乘法，那么会得到 的一个方阵 。既然 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

这样我们就可以得到矩阵 的 个特征值和对应的 个特征向量 了。将 的所有特征向量张成一个 的矩阵 ，就是我们SVD公式里面的 矩阵了。一般我们将 中的每个特征向量叫做 的右奇异向量。

如果我们将 和 的转置做矩阵乘法，那么会得到 的一个方阵 。既然 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

这样我们就可以得到矩阵 的m个特征值和对应的m个特征向量 了。将 的所有特征向量张成一个 的矩阵 ，就是我们SVD公式里面的 矩阵了。一般我们将 中的每个特征向量叫做 的左奇异向量。

和 我们都求出来了，现在就剩下奇异值矩阵 没有求出了。由于 除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值 就可以了。

我们注意到:

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵 。

上面还有一个问题没有讲，就是我们说 的特征向量组成的就是我们SVD中的V矩阵，而 的特征向量组成的就是我们SVD中的 矩阵，这有什么根据吗？这个其实很容易证明，我们以 矩阵的证明为例。

上式证明使用了: 。可以看出 的特征向量组成的的确就是我们SVD中的 矩阵。类似的方法可以得到 的特征向量组成的就是我们SVD中的 矩阵。

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系:

这样也就是说，我们可以不用 来计算奇异值，也以通过求出 的特征值取平方根来求奇异值。

SVD的性质

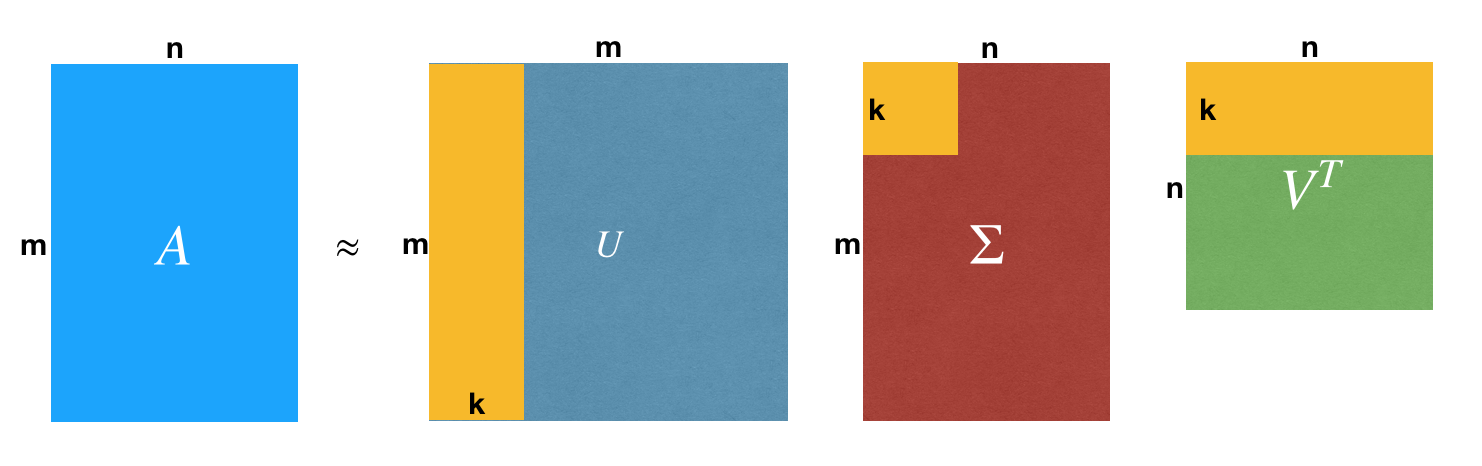
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的 个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

其中， 要比 小很多，也就是一个大矩阵 可以用三个小矩阵 来表示，如下图所示，现在我们的矩阵 只需要黄色的部分的三个小矩阵就可以近似描述了。

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

SVD用于PCA

要用PCA降维，需要找到样本协方差矩阵 的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵 ，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到我们的SVD也可以得到协方差矩阵 最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵 ，也能求出我们的右奇异矩阵 。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是 的矩阵 ，如果我们通过SVD找到了矩阵 最大的d个特征向量张成的 维矩阵 ，则我们如果进行如下处理：

可以得到一个 的矩阵 ,这个矩阵和我们原来的 维样本矩阵 相比，行数从 减到了 ，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

SVD用于推荐

一个评分矩阵 ,可做分解得到两个矩阵 和 ，如下图所示：

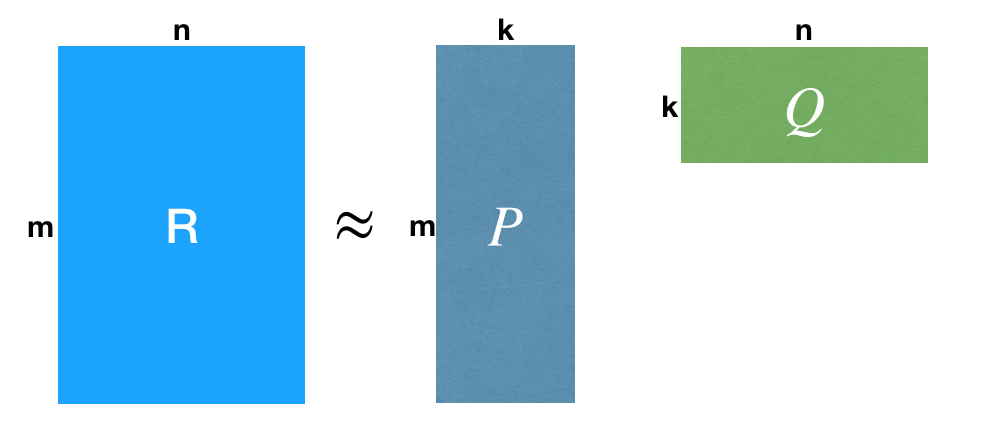
用来表示用户数， 表示物品数目。

利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分，那么未知的评分也就可以用P的某一行乘上Q的某一列得到了：

这是预测用户u对商品i的评分，它等于 矩阵的第 行乘上 矩阵的第 列。这个是最基本的SVD算法，那么如何通过已知评分训练得到 和 的具体数值呢？
假设已知评分为：

则真实值与预测值的误差为：

进而可以计算得到总的误差平方和：

只要通过训练把SSE降到最小那么P、Q就能最好地拟合R了。