运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制 。实现 LRUCache 类：

LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字-值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

进阶：你是否可以在 O(1) 时间复杂度内完成这两种操作？

  1. 输入
  2. ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
  3. [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
  4. 输出
  5. [null, null, null, 1, null, -1, null, -1, 3, 4]
  7. 解释
  8. LRUCache lRUCache = new LRUCache(2);
  9. lRUCache.put(1, 1); // 缓存是 {1=1}
  10. lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
  11. lRUCache.get(1);    // 返回 1
  12. lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
  13. lRUCache.get(2);    // 返回 -1 (未找到)
  14. lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
  15. lRUCache.get(1);    // 返回 -1 (未找到)
  16. lRUCache.get(3);    // 返回 3
  17. lRUCache.get(4);    // 返回 4

提示：

  • 1 <= capacity <= 3000
  • 0 <= key <= 3000
  • 0 <= value <= 104
  • 最多调用 3 * 104 次 get 和 put

思路

说实话，一开始我被这个题目搞的云里雾里，题目都没看懂，我tm真菜，看了题解答案，发现缓存其实就是存储hash或者链表存储，实现缓存机制。

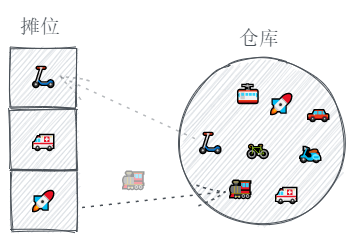
假设我们有一个玩具摊位，可以向顾客展示小玩具，但是摊位大小有限，我们不能把所有的玩具都摆在摊位上，所以我们就把大部分的玩具都放在了仓库里。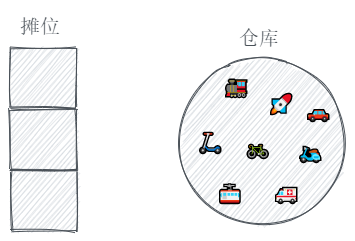
image.png

如果有顾客来问，我们就去仓库把那个玩具拿出来，摆在摊位上。

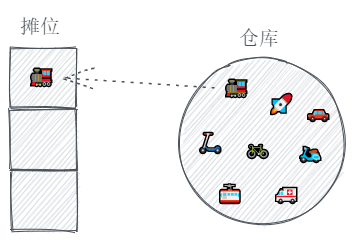
image.png

因为最上面的那个位置最显眼，所以我们想总是把最新拿出来的玩具放在那。

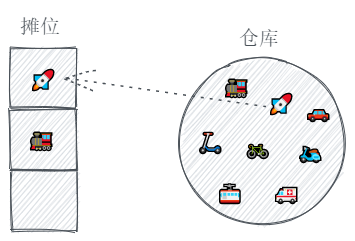
image.png

但是摊位大小有限，很快就摆满了，如果这时又来了顾客想看新玩具。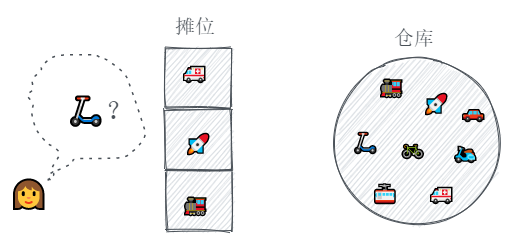
image.png

我们只能把最下面的玩具拿回仓库(因为最下面的位置相对没那么受欢迎)，腾出一个位置来放新玩具。

image.png

如果顾客想看的玩具就在摊位上，我们就可以直接展示这个玩具，同时把它放到最上面的位置(有人问说明它受欢迎嘛)，其他的玩具就要挪挪位置了。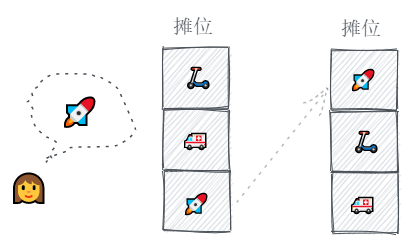
image.png

回到计算机问题上面来，我们要用什么来表示我们的玩具摊位呢，如果用数组，玩具在摊位上的位置挪来挪去的，时间复杂度得是 O(N)O(N)，所以只能用链表了。

用链表的话，随意移除一个节点的时间复杂度是 O(1)O(1)，移除节点后，我们还得把它前后两个节点连起来，所以用双向链表会比较方便。

但是链表获取节点的时间复杂度是 O(N)O(N)，我们手动移动玩具的时候，只需要看一眼就知道要找的玩具在哪个位置上，但是计算机没有那么聪明，所以我们还需要一个数据结构(哈希表)来帮计算机记录什么玩具在什么位置上。

复杂度分析
时间复杂度：O(1)O(1)。
空间复杂度：链表 O(N)O(N)，哈希表 O(N)O(N)，结果还是 O(N)O(N)。
伪代码

  1. // put
  3. if key 存在:
  4.     更新节点值
  5.     把节点移到链表头部
  7. else:
  8.     if 缓存满了:
  9.         移除最后一个节点
  10.         删除它在哈希表中的映射
  12.     新建一个节点
  13.     在哈希表中增加映射
  14.     把节点加到链表头部
  17. // get
  19. if key 存在:
  20.     返回节点值
  21.     把节点移到链表头部
  22. else:
  23.     返回 -1
  1. class DoubleLinkedListNode {
  2.     constructor(key, value) {
  3.         this.key = key;
  4.         this.value = value;
  5.         this.prev = null;
  6.         this.next = null;
  7.     }
  8. }
  10. class LRUCache {
  11.     constructor(capacity) {
  12.         this.capacity = capacity;
  13.         // Mappings of key->node.
  14.         this.hashmap = {};
  15.         // Use two dummy nodes so that we don't have to deal with the head/tail seperately.
  16.         this.dummyHead = new DoubleLinkedListNode(null, null);
  17.         this.dummyTail = new DoubleLinkedListNode(null, null);
  18.         this.dummyHead.next = this.dummyTail;
  19.         this.dummyTail.prev = this.dummyHead;
  20.     }
  22.     _isFull() {
  23.         return Object.keys(this.hashmap).length === this.capacity;
  24.     }
  26.     _removeNode(node) {
  27.         node.prev.next = node.next;
  28.         node.next.prev = node.prev;
  29.         node.prev = null;
  30.         node.next = null;
  31.         return node;
  32.     }
  34.     _addToHead(node) {
  35.         const head = this.dummyHead.next;
  36.         node.next = head;
  37.         head.prev = node;
  38.         node.prev = this.dummyHead;
  39.         this.dummyHead.next = node;
  40.     }
  42.     get(key) {
  43.         if (key in this.hashmap) {
  44.             const node = this.hashmap[key];
  45.             this._addToHead(this._removeNode(node));
  46.             return node.value;
  47.         } else {
  48.             return -1;
  49.         }
  50.     }
  52.     put(key, value) {
  53.         if (key in this.hashmap) {
  54.             // If key exists, update the corresponding node and move it to the head.
  55.             const node = this.hashmap[key];
  56.             node.value = value;
  57.             this._addToHead(this._removeNode(node));
  58.         } else {
  59.             // If it's a new key.
  60.             if (this._isFull()) {
  61.                 // If the cache is full, remove the tail node.
  62.                 const node = this.dummyTail.prev;
  63.                 delete this.hashmap[node.key];
  64.                 this._removeNode(node);
  65.             }
  66.             // Create a new node and add it to the head.
  67.             const node = new DoubleLinkedListNode(key, value);
  68.             this.hashmap[key] = node;
  69.             this._addToHead(node);
  70.         }
  71.     }
  72. }
  74. /**
  75.  * Your LRUCache object will be instantiated and called as such:
  76.  * var obj = new LRUCache(capacity)
  77.  * var param_1 = obj.get(key)
  78.  * obj.put(key,value)
  79.  */

作者：suukii
链接：https://leetcode-cn.com/problems/lru-cache/solution/146-lru-huan-cun-ji-zhi-shuang-xiang-lian-biao-ha-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。