二叉树是什么？

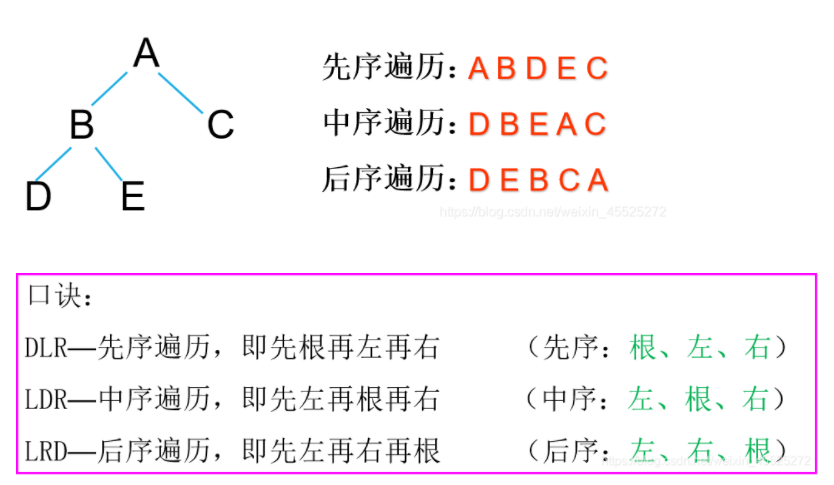
二叉树就是是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。 二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树 。

二叉树的概念

  • 根节点
  • 右子树
  • 左子树

    二叉树的实现

    ```javascript // 创建节点 class CreateNode { constructor(key){
    1.   this.key = key;
    2.   this.left = null;
    3.   this.right = null;
    } }

class Tree { constructor() { // 创建根节点 this.root = null; } set(val){ // 创建节点 let node = new CreateNode(val); // 如果根节点为空，那么要插入的节点则作为根节点 if(!this.root){ this.root = node; }else{ // 如果根节点不为空，则正常插入节点 // 当前插入的节点 | 插入节点的位置 this.addNode(node,this.root); } } addNode(node,root){ // 判断节点插入的位置 // 如果插入的节点小于上面的节点则插入到左子树 if(node.key < root.key){ // 如果要插入的节点的左子树为空，直接插入，否则往下找 if(!root.left) { root.left = node; }else{ this.addNode(node,root.left); } }

  1.     // 如果插入的字节点大于插入当前位置的节点，那么则插在右面
  2.     if(node.key > root.key){
  3.         if(!root.right){
  4.             root.right = node;
  5.         }else{
  6.             this.addNode(node,root.right)
  7.         }
  8.     }
  9.     // 返回结果
  10.     return this.root;
  11. }
  12. // 显示方法
  13. show(obj){
  14.     // for(let key in obj){
  15.     //     if(typeof obj[key] == 'object'){
  16.     //         console.log(obj[key]);
  17.     //         this.show(obj[key])
  18.     //     }else{
  19.     //         console.log(obj[key]);
  20.     //     }
  21.     // }
  22.     console.log(this.root);
  23. }

}

  1. <a name="LjjlA"></a>
  2. #### 二叉树的求最值
  3. ```javascript
  4. max(){
  5.     // 如果根节点不存在
  6.     if(!this.root) return false;
  7.     while(this.root.right){
  8.         this.root = this.root.right;
  9.     }
  10.     // 返回结果
  11.     return this.root;
  12. }

二叉树三种顺序图示

二叉树遍历图示.png

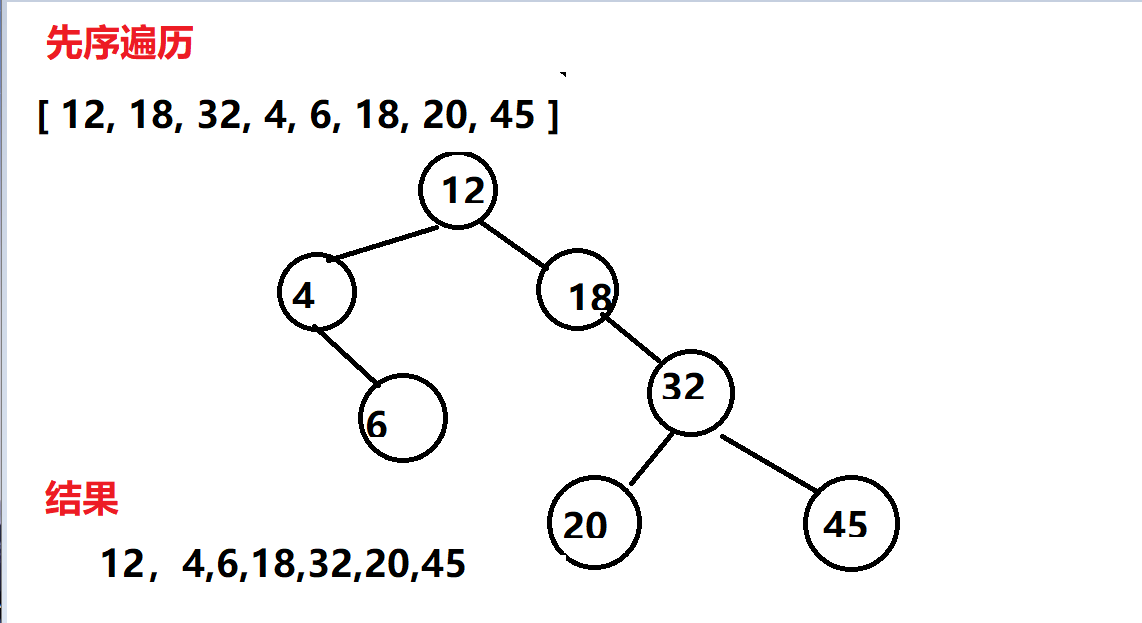
二叉树的先序

图示

binarySearchTree.png

二叉树先序的代码展示
  1. class CreateNode {
  2.     constructor(key) {
  3.         this.key = key;
  4.         this.left = null;
  5.         this.right = null;
  6.     }
  7. }
  9. class BinarySearchTree {
  10.     constructor() {
  11.         // 创建根节点
  12.         this.root = null;
  13.     }
  14.     set(arr) {
  15.         // 创建节点
  16.         arr.forEach(item => {
  17.             let node = new CreateNode(item);
  19.             // 如果根节点为空，那么要插入的节点则作为根节点
  20.             if (!this.root) {
  21.                 this.root = node;
  22.             } else {
  23.                 // 如果根节点不为空，则正常插入节点
  24.                 //      当前插入的节点 | 插入节点的位置
  25.                 this.addNode(node, this.root);
  26.             }
  27.         })
  29.     }
  30.     addNode(node, root) {
  31.         // 判断节点插入的位置
  32.         // 如果插入的节点小于上面的节点则插入到左子树
  33.         if (node.key < root.key) {
  34.             // 如果要插入的节点的左子树为空，直接插入，否则往下找
  35.             if (!root.left) {
  36.                 root.left = node;
  37.             } else {
  38.                 this.addNode(node, root.left);
  39.             }
  40.         }
  42.         // 如果插入的字节点大于插入当前位置的节点，那么则插在右面
  43.         if (node.key > root.key) {
  44.             if (!root.right) {
  45.                 root.right = node;
  46.             } else {
  47.                 this.addNode(node, root.right)
  48.             }
  49.         }
  50.         // 返回结果
  51.         return this.root;
  52.     }
  53.     // 先序遍历 先遍历根节点，然后先从左子树遍历，左子树遍历完在遍历右子树
  54.     prevTraval(callback) {
  55.         this.prevTravalNode(this.root, callback)
  56.     }
  57.     prevTravalNode(node, callback) {
  58.         // 如果节点存在，则打印该节点
  59.         if (node) {
  60.             // 调用回调
  61.             callback(node.key);
  62.             this.prevTravalNode(node.left, callback);
  63.             this.prevTravalNode(node.right, callback)
  64.         }
  65.     }
  67. }
  69. var BST = new BinarySearchTree();
  71. BST.set([12, 18, 32, 4, 6,20, 45])
  72. BST.prevTraval((val) => console.log(val))