1.题目

给你一个有 n 个服务器的计算机网络，服务器编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示服务器 ui 和 vi 之间有一条信息线路，在 一秒 内它们之间可以传输 任意 数目的信息。再给你一个长度为 n 且下标从 0 开始的整数数组 patience 。

题目保证所有服务器都是 相通 的，也就是说一个信息从任意服务器出发，都可以通过这些信息线路直接或间接地到达任何其他服务器。

编号为 0 的服务器是 主 服务器，其他服务器为 数据 服务器。每个数据服务器都要向主服务器发送信息，并等待回复。信息在服务器之间按 最优 线路传输，也就是说每个信息都会以 最少时间 到达主服务器。主服务器会处理 所有 新到达的信息并 立即 按照每条信息来时的路线 反方向 发送回复信息。

在 0 秒的开始，所有数据服务器都会发送各自需要处理的信息。从第 1 秒开始，每 一秒最 开始 时，每个数据服务器都会检查它是否收到了主服务器的回复信息（包括新发出信息的回复信息）：

如果还没收到任何回复信息，那么该服务器会周期性 重发 信息。数据服务器 i 每 patience[i] 秒都会重发一条信息，也就是说，数据服务器 i 在上一次发送信息给主服务器后的 patience[i] 秒 后 会重发一条信息给主服务器。
否则，该数据服务器 不会重发 信息。
当没有任何信息在线路上传输或者到达某服务器时，该计算机网络变为 空闲 状态。

请返回计算机网络变为 空闲 状态的 最早秒数 。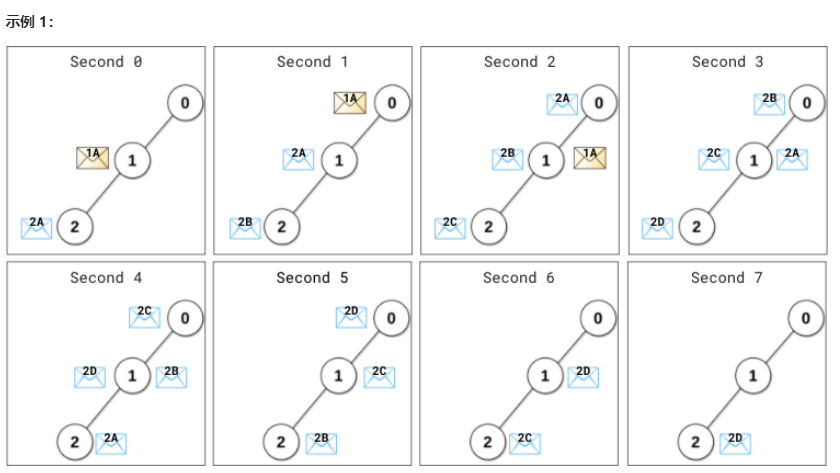
image.png

  1. 输入：edges = [[0,1],[1,2]], patience = [0,2,1]
  2. 输出：8
  3. 解释：
  4. 0 秒最开始时，
  5. - 数据服务器 1 给主服务器发出信息（用 1A 表示）。
  6. - 数据服务器 2 给主服务器发出信息（用 2A 表示）。
  8. 1 秒时，
  9. - 信息 1A 到达主服务器，主服务器立刻处理信息 1A 并发出 1A 的回复信息。
  10. - 数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒（1 < patience[1] = 2），所以不会重发信息。
  11. - 数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒（1 == patience[2] = 1），所以它重发一条信息（用 2B 表示）。
  13. 2 秒时，
  14. - 回复信息 1A 到达服务器 1 ，服务器 1 不会再重发信息。
  15. - 信息 2A 到达主服务器，主服务器立刻处理信息 2A 并发出 2A 的回复信息。
  16. - 服务器 2 重发一条信息（用 2C 表示）。
  17. ...
  18. 4 秒时，
  19. - 回复信息 2A 到达服务器 2 ，服务器 2 不会再重发信息。
  20. ...
  21. 7 秒时，回复信息 2D 到达服务器 2 。
  23. 从第 8 秒开始，不再有任何信息在服务器之间传输，也不再有信息到达服务器。
  24. 所以第 8 秒是网络变空闲的最早时刻。

image.png

2.思路

首先，信息在服务器之间按 最优 线路传输，也就是说每个信息都会以最少时间到达主服务器。这里决定信息到达主服务器时间的是服务器到主服务器的最短距离，也就是说需要求解出主服务器到每个服务器的最短距离，利用广度优先搜索在这个计算机网络构成的图内进行搜索，求解最短距离。题目要求的是整个计算机网络最早的空闲时间，那么就要求出服务器中接受到最后一条发出的消息的回复的最长时间。对于每个节点最后一条消息回复的最长时间是和其发出最后一条消息的时间以及发出消息后收到的时间相关的。假设最短距离为dist，那么对于第一条发出的消息来说，在2*dist会收到消息的回复，设服务器每过p秒会重新发送消息那么：

  • 当2dist<=p时，说明服务器仅发出一条消息，对于服务器来说，在2dist+1时网络中流动的信息就与它无关了。
  • 当2dist>p时，说明服务器不止发出了一条消息，需要找出最后一条消息的发送时间。题目中说明了当收到消息回复后就不会再发送消息了即收到第一条发送出去的消息的回复后不再发送消息，那么在2dist内会发送（2dist-1）/p条消息，最后一条消息的发送时间应该是pint(（2dist-1）/p)，最后一条消息的回复时间应该是pint(（2dist-1）/p)+2dist+1，记为time.当2*dist<=p时也满足该式。

最后的结果就是最大的time。

3.代码

class Solution {
public:
    int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
        int n = patience.size();
        int ans = 0, dist = 1;
        vector<vector<int>> adj(n);
        vector<bool> visit(n,false);
        queue<int> q;

        //创建邻接表，和visit表组合使用取最短距离
        for(auto e:edges)
        {
            adj[e[0]].emplace_back(e[1]);
            adj[e[1]].emplace_back(e[0]);
        }
        //广度遍历，距离由段到长，依次根据邻接表访问获得最短距离，进一步依据最后一次发送消息时间获取相应的时长
        q.emplace(0);
        visit[0] = true;
        while(!q.empty())
        {
            int sz = q.size();
            for(int i = 0; i < sz; i++)
            {
                int curr = q.front();
                q.pop();
                for(auto v:adj[curr])
                {
                    if(visit[v])
                        continue;
                    q.emplace(v);
                //cout << v << endl;
                    int time = ((2*dist-1)/patience[v])*patience[v]+2*dist+1;
                    ans = max(ans, time);
                    visit[v] = true;
                }
            }
            dist++;
        }
        return ans;
    }
};