2021.01.21 二进制中1的个数
今日题目:请实现一个函数,输入一个整数(以二进制串形式),输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。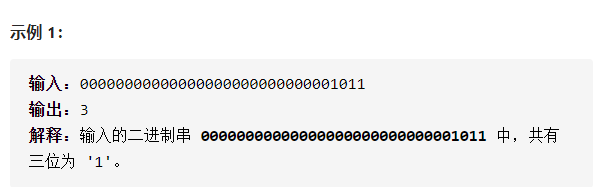
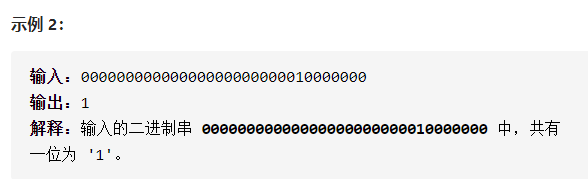
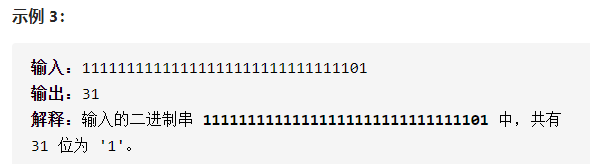
提示:输入必须是长度为 32 的 二进制串 。
- 思路:救命,这题好烦。写生气了。
- 法一:暴力法。分为正数与负数进行处理。(想的太复杂了55555)时间复杂度为O(n),空间复杂度为O(1)
- 正数:当n > 1时,对2取余,若为1,则count(计数器)++,最后再进行count ++。
- 负数:令n=n的相反数,把n的二进制表示分为两部分,以最右边的一个1为分界线,进行两个阶段的处理。例:00001000,设置一个布尔值tag用来区分两个阶段,同时用一个length来记录位数。第一阶段:先对2取余,一直到n>1且余数为1的情况,修改tag的值进入第二阶段。第二阶段:依旧是对2取余,若余数为0则count(计数器)++。每算出一位,length就进行加1。最后length再进行加一,若n是奇数则进行count++,1的个数就是32 - length + count。
- 法二:偷懒,直接调用Integer类中的bitCount()方法orz。
- 法三:逐位判断。因为提示说把n当作无符号数进行处理,则采用无符号右移的方式。n & 1== 0(n的最后一位为0),n & 1 ==1(n的最后一位为1)。时间复杂度为O(logn),空间复杂度为O(1)。
- 法四:大佬神了。设置一个计数器count用于记录1的数量,以n != 0为条件,令n = n & (n - 1); n & (n - 1)操作可以消掉n最右边的1。时间复杂度为O(M),M为1的个数,空间复杂度为O(1)。
- 法一:暴力法。分为正数与负数进行处理。(想的太复杂了55555)时间复杂度为O(n),空间复杂度为O(1)
注意:哈哈哈 n&(n-1) 还可以用来判断 n 是否是 2 的幂~
- 自己的菜鸡代码:
```java
// 法一
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
} }// int 类型有4B,为32位,为有符号整数,所以要把十进制数转为二进制数再确定1的个数// count 用于统计1的个数int count = 0;// 正数//System.out.println(n);if(n > 0){while(n > 1){if(n % 2 == 1) ++count;n = n / 2;}++count;}else if(n < 0){// 负数if(n == -2147483648) return 1;n = 0 - n;boolean tag = false;int length = 0;while(n > 1){++length;if(!tag && n % 2 == 1) {++count;tag = true;}if(tag && n % 2 == 0) ++count;n = n / 2;}if(!tag) ++count;++length;count = 32 - length + count;}return count;
// 法二 public class Solution { // you need to treat n as an unsigned value public int hammingWeight(int n) { int res = 0; while(n != 0){ res += n & 1; n >>>= 1; } return res; } }
// 法三 public class Solution { // you need to treat n as an unsigned value public int hammingWeight(int n) { int res = 0; while(n != 0){ res += n & 1; n >>>= 1; } return res; } }
// 法四
- 运行结果:法一(左)、法二(右)<br /><br />法三(左)、法四(右)<br /><a name="WaXOw"></a>### 2021.01.21 2的幂今日题目:给定一个整数,编写一个函数来判断它是否是 2 的幂次方。<br />- 思路:利用上面问题中的 n & (n - 1),在n > 0时,若n为2的幂,则n & (n - 1)的结果为0,否则不为0。(大佬太强悍了)- 自己的菜鸡代码:```javaclass Solution {public boolean isPowerOfTwo(int n) {return n > 0 && (n & (n - 1)) == 0;}}
- 运行结果:
2021.01.25 不用加减乘除做加法
今日题目:写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
提示:
- a, b 均可能是负数或 0
结果不会溢出 32 位整数
思路:因为题目中明确说明不能用“+”、“-”、“*”、“/” 四则运算符号,所以很明显就是用位运算,用value来记录结果值,用 c 记录每一位运算的进位情况,用res_a、res_b记录a 与 b的每一位。这个问题有一些棘手的地方:
- 因为是逐位运算,所以需要记录已计算的位数:
因为不能用加法,所以不能使用普通的记录值,-2147483648在java中的存储形式为 80000000H,每计算完一位,就将count逻辑右移一位,当count == 0时代表已经运算完毕,直接将value返回就好。
- 如何记录每一位的运算值:
- 运算过程:(1+2)0000……0001 + 0000……0010 6
初始化:
int value = 0; int c = 0;
int res_a = 0, res_b = 0;
int count = -2147483648;
循环条件:count != 0
先获得a、b当前位的值(a、b分别和 1 相与),
并将value右移一位
图中空白处默认为0
刚刚开始的时候: 
value右移一位之后此时res_a = 1,res_b = 0,c = 0;
开始计算,分为 4 种情况:
1. 当res_a + res_b + c ==0:c = 0; 1. 当res_a + res_b + c ==1:value = value | -2147483648;c = 0; 1. 当res_a + res_b + c ==2:c = 1; 1. 当res_a + res_b + c ==3:value = value | -2147483648;c = 1; 
这一轮计算完毕之后,将a、b、count逻辑右移一位。
然后继续运算。 依次类推。
依次类推。
- 时间复杂度:O(n),空间复杂度O(1)。
自己的菜鸡代码:
class Solution {public int add(int a, int b) {// 位运算,Java内部是以整数补码存储,模拟二进制运算(不能用 + 号 giao)int value = 0;int c = 0;int res_a = 0, res_b = 0;int count = -2147483648;// 循环停止的条件是 a 与 b 同时为 0while(count != 0){//获得a的最后一位res_a = a & 1;//获得b的最后一位res_b = b & 1;value >>>= 1;if(res_a == 1 && res_b == 1){if(c == 0){// // res_a + res_b + c == 2c = 1;}else{// res_a + res_b + c == 3value = value | -2147483648;c = 1;}}else if(res_a == 0 && res_b == 0){if(c == 1){// res_a + res_b + c == 1value = value | -2147483648;c = 0;}}else{if(c == 0){// res_a + res_b + c == 1value = value | -2147483648;c = 0;}else{// res_a + res_b + c == 2c = 1;}}a >>>= 1;b >>>= 1;count >>>= 1;}return value;}}
运行结果:
2021.02.15 两数之和
今日题目:不使用运算符 + 和 - ,计算两整数 a 、b 之和。
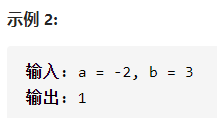
- 思路:这题很明显就是使用位运算,跟上一题一样,但是看了大佬的思路发现有更简便的方法。异或操作可以得到两个数无进位的加法结果,与操作可以得到两个数的进位情况。
如:3+9 = 12
0011 & 1001 = 0001 0011 XOR 1001 = 1010
随后需要将无进位的加法结果加上进位结果,所以需将进位结果左移一位再相加。
循环结束的条件就是进位结果为0;
自己的菜鸡代码:
class Solution {public int getSum(int a, int b) {while(b != 0){// 得到进位结果int c = a & b;// 进位结果左移一位c = (c <<= 1);// 得到无进位的加法结果a = a^b;// 保存进位结果b = c;}return a;}}
运行结果: