栈与队列 - 《算法刷题心得》

2021.01.02 滑动窗口的最大值
2021.01.05 用两个栈实现队列
2021.01.07 包含min函数的栈。（有点难）
2021.01.08 栈的压入、弹出序列。（有点难，俺好菜）

2021.01.02 滑动窗口的最大值

今日题目：给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。

思路：
1. 法一：用一个数组记录滑动窗口内的最大值，然后直接用暴力法找出每个滑动窗口内的最大值。时间复杂度为O(n)，空间复杂度为O(n)。
2. 法二：大佬的代码是用双端队列解决的。先判断数组是否为空或者数组长度为1，若是，则直接返回数组；定义一个双端队列（存放的是对应的数组下标而不是数据本身），遍历数组中各元素，在队列不空的情况下，与队尾元素进行比较，若是大于等于队尾元素，队尾元素就出队，一直到队列空或者小于队尾元素，则插入队尾。判断此时队首元素是否失效（即是否已位于滑动窗口外），若已失效，则出队。再判断是否已经遍历完整个滑动窗口，若是则保存队首元素（此滑动窗口的最大值）。

自己的菜鸡代码

// 法一
class Solution {
  public int[] maxSlidingWindow(int[] nums, int k) {
      // 暴力法解决
      if(nums.length < 2) return nums;
      int []record = new int[nums.length - k + 1];
      int max, j;
      for(int i = 0; i < record.length; i++){
          max = Integer.MIN_VALUE;
          for(j = i; j < i + k; j++){
              if(nums[j] > max) max = nums[j];
          }
          record[i] = max;
      }
      return record;
  }
}

正确解法：采用双端队列

思路见下边代码的注解（俺太菜了，大佬的代码看懂了但是也不一定会用）

// 法二
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 先判断数组是否为空或者数组长度为1，若是，则直接返回数组
        if(nums == null || nums.length < 2) return nums;
        // 结果数组
        int a[] = new int[nums.length - k + 1];
        // 双端队列（存放的是对应的数组下标而不是数据本身）
        LinkedList<Integer> queue = new LinkedList();
        // 遍历数组中各元素
        for(int i = 0; i < nums.length; i++){
            // 判断队列中是否为空，若不空，再将此时遍历到的元素nums[i]从队尾开始向前比较
            // 遇到比nums[i]小的数，一律弹出，直到遇到比它大的或者队列为空
            while(!queue.isEmpty() && nums[queue.peekLast()] <= nums[i]){
                queue.pollLast();
            // 队尾插入nums[i]对应的数组下标
            queue.addLast(i);
            // 若此时队首元素不在滑动窗口内，则弹出队首元素
            if(queue.peek() <= i-k) queue.poll();
            // 是否遍历完整个滑动窗口，若是则将队首元素（此时滑动窗口的最大值）存入结果数组中
            if(i-k+1 >= 0) a[i-k+1] = nums[queue.peek()];
        }
        return a;
    }
}

运行结果：
法一（左），法二（右）

2021.01.05 用两个栈实现队列

今日题目：用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )
提示：1 <= values <= 10000，最多会对 appendTail、deleteHead 进行 10000 次调用

思路：因为java中stack的容量会自动增长，初始值为10。因此入队操作不用考虑容量，出队操作时，可以先把s1中的数据全部存入s2中，s2栈顶元素即队首元素。
1. 版本一：入队操作即s1栈的入栈操作，出队操作——先把s1中的数据全部存入s2中，弹出s2的栈顶元素，再把s2中的全部数据重新存入s1中。这样子大部分时间都用于s1与s2之间数据的存放。
2. 版本二：入队操作即s1栈的入栈操作；出队操作——若s2中为空，则将s1中的数据全部存入s2中，弹出s2的栈顶元素，此时不再存入s1中，出队操作即s2的出栈操作；若s2中不为空，则直接执行s2的出队操作。（这样子应该可以省不少时间）
自己的菜鸡代码：

// 第一版，时间花费太多
class CQueue {
    Stack<Integer> s1;
    Stack<Integer> s2;
    public CQueue() {
        // 初始化操作
        this.s1 = new Stack<Integer>();
        this.s2 = new Stack<Integer>();
    }
    public void appendTail(int value) {
        // 实现入队操作，因为java中的stack容量会自动增长，初始值为10
        s1.push(value);
    }
    public int deleteHead() {
        // 实现出队操作
        int result;
        if(!s1.isEmpty()){
            while(!s1.isEmpty()){
                s2.push(s1.peek());
                s1.pop();
            }
            result = s2.peek();
            s2.pop();
            while(!s2.isEmpty()){
                s1.push(s2.peek());
                s2.pop();
            }
        }else{
            result = -1;
        }
        return result;
    }
}
/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */
// 第二版，时间应该会少很多（flag先立）===========================================
class CQueue {
    Stack<Integer> s1;
    Stack<Integer> s2;
    public CQueue() {
        // 初始化操作
        this.s1 = new Stack<Integer>();
        this.s2 = new Stack<Integer>();
    }
    public void appendTail(int value) {
        // 实现入队操作，因为java中的stack容量会自动增长，初始值为10
        s1.push(value);
    }
    public int deleteHead() {
        int result;
        if(!s2.isEmpty()){
            result = s2.peek();
            s2.pop();
        } else{
            if(s1.isEmpty()) return -1;
            while(!s1.isEmpty()){
                s2.push(s1.peek());
                s1.pop();
            }
            result = s2.peek();
            s2.pop();
        }
        return result;
    }
}
// 力扣官方出的====================================================================
class CQueue {
    Deque<Integer> stack1;
    Deque<Integer> stack2;
    public CQueue() {
        stack1 = new LinkedList<Integer>();
        stack2 = new LinkedList<Integer>();
    }
    public void appendTail(int value) {
        stack1.push(value);
    }
    public int deleteHead() {
        // 如果第二个栈为空
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        } 
        if (stack2.isEmpty()) {
            return -1;
        } else {
            int deleteItem = stack2.pop();
            return deleteItem;
        }
    }
}

运行结果（版本一）：zhwm级别的慢，感觉老人家走路都比这个快。
运行结果（版本二）：怎么还是这么慢？？

运行结果（官方版本的）：

跟力扣官方版本的主要区别就是数据结构用的不太一样，但是现在我还不能很准确地给出这两个数据结构之间的不同。

2021.01.07 包含min函数的栈。（有点难）

今日题目：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。
要降低时间复杂度无非就使用空间换时间，主要就是看如何换使得花费的空间更少就是了。

提示：各函数的调用总次数不超过 20000 次

思路：（自己想不出来，卡在了当目前最小值被pop出去后如何在O(1)的时间复杂度情况下求栈中的最小值，俺好菜，好了，俺想到可以用辅助栈，每push一个数，就在辅助栈中记录当前栈的最小值。）大佬的算法中没有用到辅助栈，也没有用java自带的stack类型（空间复杂度不如直接用数组但是很方便）。先初始化栈，min = Integer.MAX_VALUE；而后执行push()操作时，先比较min与要入栈值x的大小，若x大于min则直接入栈，否则先将原min值入栈，然后min = x，再将x入栈。出栈的时候判断栈顶元素是否等于min值，若是，则先pop，然后使min = data[top]，若是不相等则直接pop。

示意图（是这么个想法）：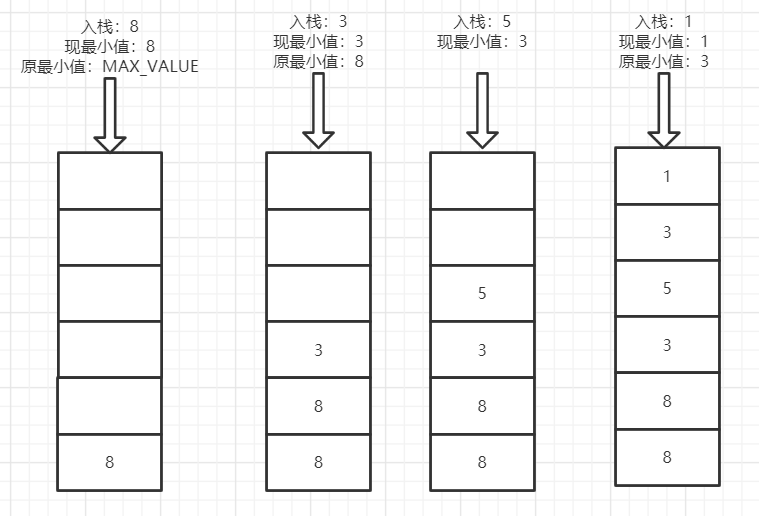

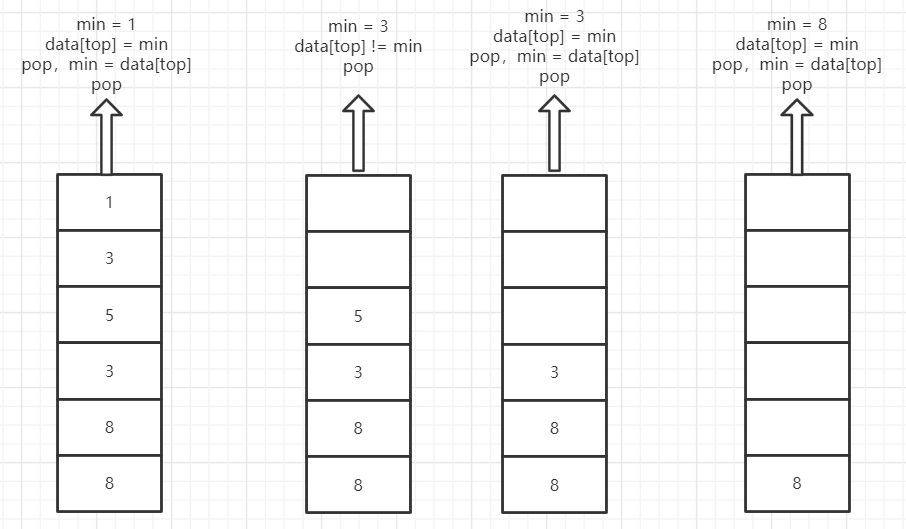
自己的菜鸡代码： ```java class MinStack { // 这个算法题最难的就是push和pop这两个方法 // 不用考虑栈为空的情况吗 private int data[]; // 用一个数组作为数据栈 private int top; // 栈顶指针 private int min; // 记录最小值 private int maxSize; // 最大长度

/* initialize your data structure here. / public MinStack() {
```
  maxSize = 10000;
  data = new int[maxSize];
  top = -1;
  min = Integer.MAX_VALUE;
```
}

public void push(int x) {
```
  if(x <= min) {
      data[++top] = min;
      min = x;
  }
  data[++top] = x;
```
}

public void pop() {
```
  // 栈为空
  //if(top == -1) return;
  if(min == data[top]){
      min = data[--top];
  }
  --top;
```
}

public int top() {
```
  // 栈为空
  //if(top == -1) return null;
  return data[top];
```
}

public int min() {
```
  return min;
```
} }

/**

Your MinStack object will be instantiated and called as such:
MinStack obj = new MinStack();
obj.push(x);
obj.pop();
int param_3 = obj.top();
int param_4 = obj.min(); */ ```

运行结果：

2021.01.08 栈的压入、弹出序列。（有点难，俺好菜）

今日题目：输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

提示：

0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列
思路：（看了题解的，神奇，有点难理解）使用一个辅助栈，一个序列索引 i 来模拟栈 stack 的输入输出。遍历pushed数组，对于遍历到的数组元素num先入栈，再循环判断栈顶元素是否等于popped[i]，若相等，则执行pop与i++；若不相等则对下一个pushed元素做相同处理。时间复杂度为：O(n)；空间复杂度为O(n)。

自己的菜鸡代码： ```java // 用java自带的Stack类型 class Solution { public boolean validateStackSequences(int[] pushed, int[] popped) {

  if(pushed.length < 2) return true;
  Stack<Integer> stack = new Stack<Integer>();
  int i = 0;
  for(int num: pushed){
      stack.push(num);
      while(!stack.isEmpty() && stack.peek() == popped[i]){
          stack.pop();
          ++i;
      }
  }
  return stack.isEmpty();

} }

// 用数组实现 class Solution { public boolean validateStackSequences(int[] pushed, int[] popped) { if(pushed.length < 2) return true; //Stack stack = new Stack(); int []stack = new int[pushed.length]; int i = 0, top = -1; for(int num: pushed){ stack[++top] = num; while(top != -1 && stack[top] == popped[i]){ —top; ++i; } } return top < 0; } }


- 运行结果（左为用Stack类，右为用数组模拟栈实现）：
![image.png](https://cdn.nlark.com/yuque/0/2021/png/1584832/1610074054163-5aafdf6d-0cc7-41be-b5c9-398c6f9f4425.png#align=left&display=inline&height=224&margin=%5Bobject%20Object%5D&name=image.png&originHeight=448&originWidth=666&size=29122&status=done&style=none&width=333)![image.png](https://cdn.nlark.com/yuque/0/2021/png/1584832/1610074031801-bc5c982b-0d29-412a-aac4-c25ce8cbbb19.png#align=left&display=inline&height=227&margin=%5Bobject%20Object%5D&name=image.png&originHeight=454&originWidth=659&size=29194&status=done&style=none&width=329.5)
<a name="T9JR4"></a>
### 2021.01.08 反转单词顺序
今日题目：输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串"I am a student. "，则输出"student. a am I"。<br />![image.png](https://cdn.nlark.com/yuque/0/2021/png/1584832/1610075831875-71fc1096-58d6-4d86-b44c-f083108f46ef.png#align=left&display=inline&height=404&margin=%5Bobject%20Object%5D&name=image.png&originHeight=473&originWidth=632&size=23847&status=done&style=none&width=540)<br />说明：
- 无空格字符构成一个单词。
- 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
- 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。
- 思路：
   1. 法一：可以用StringBuilder类来实现，先对字符串采取消除首尾空格的操作，对字符串从后往前遍历，每遇到一个单词，就截取下来加上一个空格加入StringBuilder的末尾最后再消除首尾空格。
   1. 法二：利用java自带的字符串分割函数，分割后再进行拼接，但是这种方法在面试的时候最好不要用（不过确实好好用）。
法一法二的时间复杂度都为O(n)，空间复杂度都为O(n)。
- 自己的菜鸡代码：
```java
// 改动前
class Solution {
    public String reverseWords(String s) {
        if(s == null) return s;
        s = s.trim();
        StringBuilder sentence = new StringBuilder();
        int j = s.length() - 1;
        for(int i = s.length() - 1; i >= 0;){
            j = i;
            while(i >= 0 && s.charAt(i) != ' ') --i;
            sentence.append(s.substring(i+1, j+1) + " ");
            while(i >= 0 && s.charAt(i) == ' ')--i;
        }
        return sentence.toString().trim();
    }
}
// 法二
class Solution {
    public String reverseWords(String s) {
        String []str = s.trim().split(" ");
        StringBuilder sentence = new StringBuilder();
        for(int i = str.length - 1; i >= 0; i--){
            if(str[i].equals("")) continue;
            sentence.append(str[i]);
            sentence.append(" ");
        }
        return sentence.toString().trim();
    }
}

运行结果：