一次面试中的缓存设计 - 《Tech Blog》

前言
题目分析设计
实现代码
简单版本

前言

尝试面试微软的暑期实习，结果在终面的时候被一道设计题给干趴了。本来以为会和之前几面一样上来丢个算法题做就是了，没想到突然来情境设计，弄得我当时的节奏有点乱了😑。面试后，我也尝试着去重新思考该题，但多次尝试都没有什么比较好的思路。最近，或许是因为空气被绵绵春雨洗刷得更加清新，使得我最近头脑比较清醒，致使我在图书馆窗边发呆的时候，突然又思考起这道题，然后灵光乍现。

题目分析设计

现在开始进入正题：

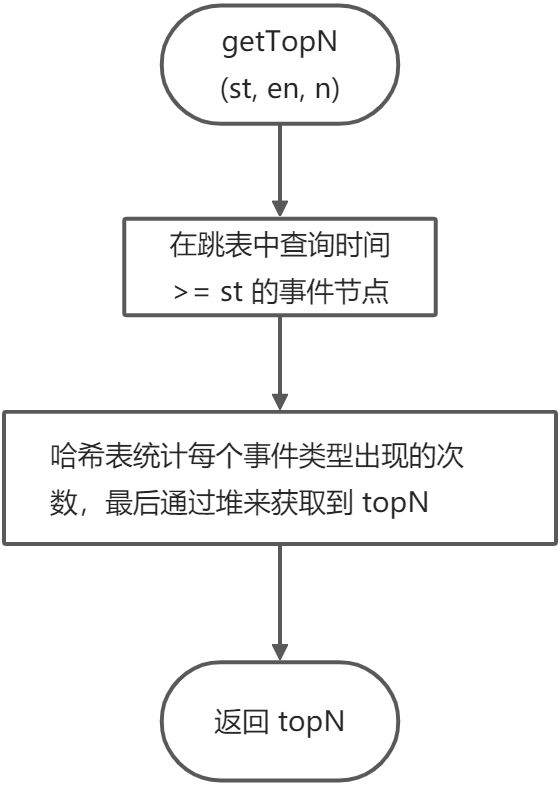
设计一个缓存，用于存储事件。每一个事件有两个主要的属性：事件类型、发生时间。接着，这个缓存需要提供一个方法 getTopN(st, en, n)，该方法获取时间窗口 [st，en] 中出现频率最高的 n 个事件类型。时间复杂度和空间复杂度越优越好。

从题目看，事件的结构已经非常明显了，就是包含 type、time 两个字段。主要难点在于，如何组织这些事件来方便之后快速地定位一个时间窗口，更直白一点就是要方便根据 time 这个字段进行范围查询。一说到范围查询我就想到了数据库的范围查询，然后想到了 B+ 树，嘿，思维就是这么跳跃。但是面试当场写 B+ 树的话，对于我而言就是作死……接着，联想同样与 B+ 树一样能够范围查询的数据结构：

平衡二叉搜索树。树搜索比较高效，能够支持范围查询，单查询的过程是树搜索，涉及到深搜回溯之类的，总感觉范围查询得不够优雅纯粹，而且实现起来也是比较麻烦，暂时不作为选择。
跳表。跳表实际上就是在链表的基础上建立了索引，使之能够支持类似二分查找的过程，所以搜索效率也高。更好的一点是，跳表对范围查询的支持很好！要得到一个 [st, en] 的时间窗口的话，就在跳表中查找到时间 st，接着顺序向后遍历即可。所以，使用跳表作为这个事件缓存的数据结构。

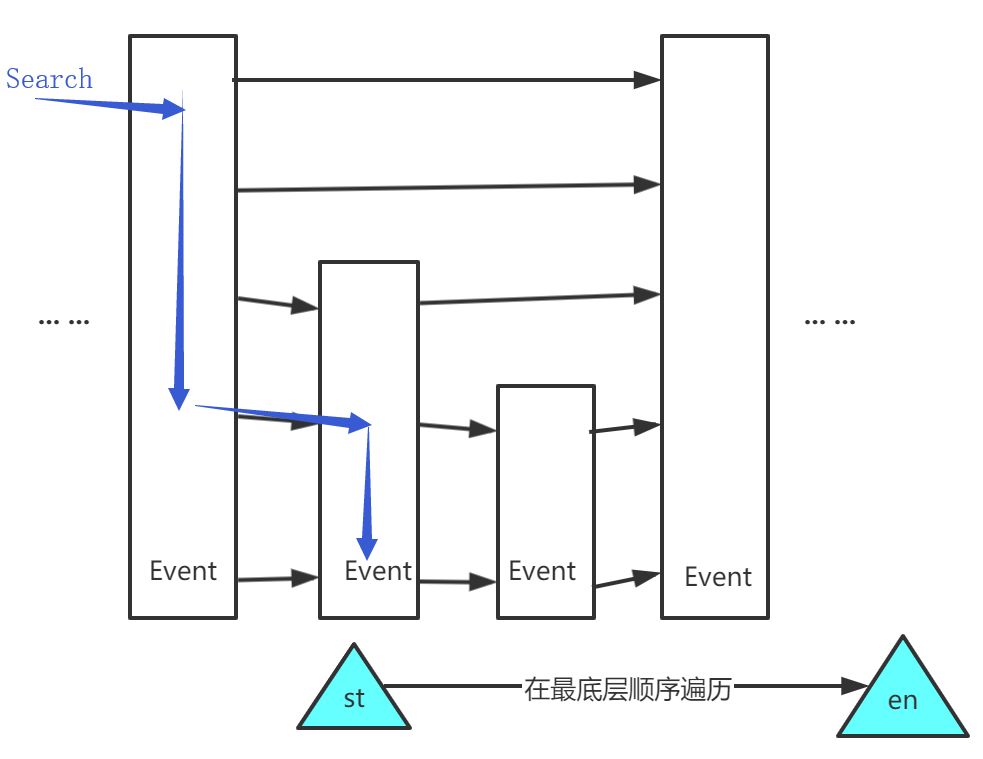
这样，定位一个时间窗口的问题就解决了，查询窗口下界的时间基本和二分查找一样是 logN。

接着，要获取时间窗口内的 topN 个事件类型。这个看似简单，但似乎也没有想到什么比较好的方法，目前的思路就是将这个区间的所有事件按照类型关键字排序，然后再顺序遍历一遍。这样的时间复杂度为 O(NlgN)，由于不能破坏原本的存储，所以需要对这个区间进行一次拷贝，故空间复杂度需要为 O(N)。另一种方案是，采用哈希表来进行统计，最后取出哈希表的元素进行排序，最终的复杂度也是一致的。

所以，总体的设计就是：

事件以 time 作为关键字，用跳表组织。
getTopN 时查询跳表，定位到时间窗口的下界。
使用哈希表统计各个类型的出现次数。
维护一个大小为 N 的堆，将哈希表的所有元素放入。

一次面试中的缓存设计 - 图3

实现代码

代码还是比较多的，感觉面试时要写出来还是比较困难……之后会展示更容易实现的一种方式。

public class EventCache {
    class Event implements {
        int time; // 事件发生时间
        int type; // 事件发生类型
    }
    // 跳表进行范围查询，解决时间窗口的问题
    class SkipList {
        private int MAX_LVL = 32;
        private Node head = new Node(null, 32);
        private int lvlCnt = 1; // 跳表的总层数
        class Node {
            Event e;
            Node[] nexts; // 向后指针
            int maxLvl; // 节点的最高层级
            Node(Event e, int maxLvl) {
                this.nexts = new Node[maxLvl];
                this.maxLvl = maxLvl;
                this.e = e;
            }
        }
        // 每高一层都要少 50% 的概率，即
        // 50% 的概率 1 层，25% 的概率 2 层，
        // 12.5% 的概率 3 层
        private int randomLvl() {
            int lvl = 1;
            while (Math.random() < 0.5f && lvl < MAX_LVL) {
                lvl += 1;
            }
            return lvl;
        }
        public void insert(Event e) {
            int lvl = randomLvl();
            this.lvlCnt = Math.max(lvlCnt, lvl);
            Node n = new Node(e, lvl);
            Node[] needUpdates = new Node[lvl];
            Node p = head, next;
            // 从最高层开始 自顶向下插入新的节点
            for (int i = lvlCnt - 1; i >= 0; i--) {
                while (p.maxLvl > i && 
                       (next = p.nexts[i]) != null && next.e.time < e.time) {
                    p = next;
                }
                if (i < lvl) {
                    needUpdates[i] = p;
                }
            }
            for (int i = 0; i < lvl; i++) {
                n.nexts[i] = needUpdates[i].nexts[i];
                needUpdates[i].nexts[i] = n;
            }
        }
        // 查找时间 >= time 的第一个事件
        public Node findGtEq(int time) {
            Node p = head, next;
            for (int i = lvlCnt - 1; i >= 0; i--) {
                while (p.maxLvl > i && 
                       (next = p.nexts[i]) != null && next.e.time < time) {
                    p = next;
                }
            }
            return p.nexts[0];
        }
    }
    private SkipList cache = new SkipList();
    public List<Integer> getTopN(int st, int en, int n) {
        // 跳表进行范围查询
        SkipList.Node node = cache.findGtEq(st);
        // K:事件类型 V:出现次数
        Map<Integer, Integer> map = new HashMap<>(); 
        while (node != null && node.e.time <= en) {
            map.put(node.type, map.getOrDefault(node.type, 0) + 1);
            node = node.nexts[0];
        }
        // 最小堆
           PriorityQueue<Entry<Integer, Integer>> pq = new PriorityQueue<>((e1, e2) -> {
            return e1.getValue() - e2.getValue();
        });
        for (Entry<Integer, Integer> e : map.entrySet()) {
            pq.offer(e.getValue());
            if (pq.size() > n) {
                 pq.poll();   
            }
        }
        return pq.stream().map(e -> e.getValue()).collect(Collectors.toList());
    }
}

简单版本

跳表的确是一个比较好的平衡查找与插入的数据结构，但是如果在面试的时候实现确实比较困难。由于时间总是递增的，所以以时间为关键字插入的时候，可以基本假设大部分情况有序。

这种情况可以使用插入排序的思想，每来一个新元素，就从后往前插入到其应在的位置，大部分情况就是直接末尾添加。由于还要支持区间的快速定位，所以可以考虑使用动态数组来实现，因为如果是末尾添加的话，除开拓容复制，动态数组添加元素也是比较高效的。

// Use ArrayList + binary search instead of SkipList,
// which is less tricky to code.
public static class Event {
    int time;
    int type;
    Event(int time, int type) {
        this.time = time;
        this.type = type;
    }
}
private List<Event> events = new ArrayList<>(); // dynamic array
// top k in [a, b]
public List<Integer> topK(int a, int b, int k) {
    int l = binSearch(a);
    int r = binSearch(b); 
    List<Integer> res = new ArrayList<>();
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = l; i <= r; i++) {
        Event e = events.get(i);
        if (e.time > b) break;
        map.put(e.type, map.getOrDefault(e.type, 0) + 1);
    }
    PriorityQueue<Entry<Integer, Integer>> pq = 
        new PriorityQueue<>((e1, e2) -> e2.getValue() - e1.getValue()); // great heap
    for (Entry<Integer, Integer> e: map.entrySet()) {
        pq.offer(e);
    }
    for (int i = 0; i < k; i++) {
        if (pq.isEmpty()) return res;
        res.add(pq.poll().getKey());
    }
    return res;
}
// insert sort
public void happen(int time, int type) {
    Event e = new Event(time, type);
    for (int i = events.size() - 1; i >= 0; i--) {
        if (e.time >= events.get(i).time) {
            events.add(i + 1, e);
            return;
        }
    }
    events.add(0, e);
}
// return index, where event's time >= t 
private int binSearch(int t) {
    int l = 0, r = events.size() - 1;
    int index = 0;
    while (l <= r) {
        int mid = l + (r-l)/2;
        if (events.get(mid).time >= t) {
            index = mid;
            r = mid - 1;
            continue;
        }
        l = mid + 1;
    }
    return index;
}