时间复杂度

什么是时间复杂度

  • 算法的时间效率
  • 算法的执行时间与算法的输入值之间的关系

1) 时间频度
算法需要花费的时间，和它语句执行的次数是成正比例的，因此把一个算法中的语句执行次数称为语句频度或时间频度，记为T(n)。
2) 时间复杂度
在上面提到的时间频度 T(n) 中，n 是指算法的规模，n 不断的变化，T(n) 就会不断的变化，为了衡量 T(n) 随 n 的变化规律，引入了时间复杂度的概念。

什么是时间复杂度，从数学的角度给出定义：
算法中某个函数有 n 次基本操作重复执行，用 T(n) 表示，现在有某个辅助函数 f(n)，使得当 n 趋近于无穷大时，T(n)/f(n) 的极限值为不等于零的常数，则称 f(n) 是 T(n) 的同数量级函数。记作 T(n) = O(f(n))，称 O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。
简要的说，就是找一个与 T(n) 同一数量级的函数 f(n) ，然后写成 O(f(n)) 就可以了。

大 O 表示法

T(n) = O(f(n))

常见时间复杂度案例分析

常数阶 O(1)

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是 O(1)

  1. int i = 1;
  2. int j = 2;
  3. ++i;
  4. j++;
  5. int m = i + j;

上述代码在执行的时候，它消耗的时间并不随着某个变量的增长而增长，那么无论这类代码有多长都可以用 O(1) 来表示它的时间复杂度。

线性阶 O(n)

  1. for(i=1; i<=n; ++i)
  2. {
  3.    j = i;
  4.    j++;
  5. }

这段代码，循环里面的代码会执行 n 遍，因此它消耗的时间是随着 n 的变化而变化的，因此这类代码都可以用 O(n) 来表示它的时间复杂度。

对数阶 O(logN)

  1. int i = 1;
  2. while(i < n)
  3. {
  4.     i = i * 2;
  5. }

上述代码在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。我们试着求解一下，假设循环 x 次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2^n，也就是说当循环 log2^n 次以后，这个代码就结束了。因此这个代码的时间复杂度为：O(logn)

线性对数阶 O(nlogN)

  1. for(m=1; m<n; m++)
  2. {
  3.     i = 1;
  4.     while(i<n)
  5.     {
  6.         i = i * 2;
  7.     }
  8. }

线性对数阶 O(nlogN) 其实非常容易理解，将时间复杂度为 O(logn) 的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是 O(nlogN)

平方阶 O(n²)

  1. for(x=1; i<=n; x++)
  2. {
  3.    for(i=1; i<=n; i++)
  4.     {
  5.        j = i;
  6.        j++;
  7.     }
  8. }

平方阶 O(n²) 就更容易理解了，如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²) 了
这段代码其实就是嵌套了 2 层 n 循环，它的时间复杂度就是 O(n*n)，即 O(n²)
如果将其中一层循环的 n 改成 m，

  1. for(x=1; i<=m; x++)
  2. {
  3.    for(i=1; i<=n; i++)
  4.     {
  5.        j = i;
  6.        j++;
  7.     }
  8. }

那它的时间复杂度就变成了 O(m*n)

立方阶 O(n³)、K次方阶 O(n^k)

参考上面的 O(n²) 去理解就好了，O(n³) 相当于三层 n 循环，其它的类似。

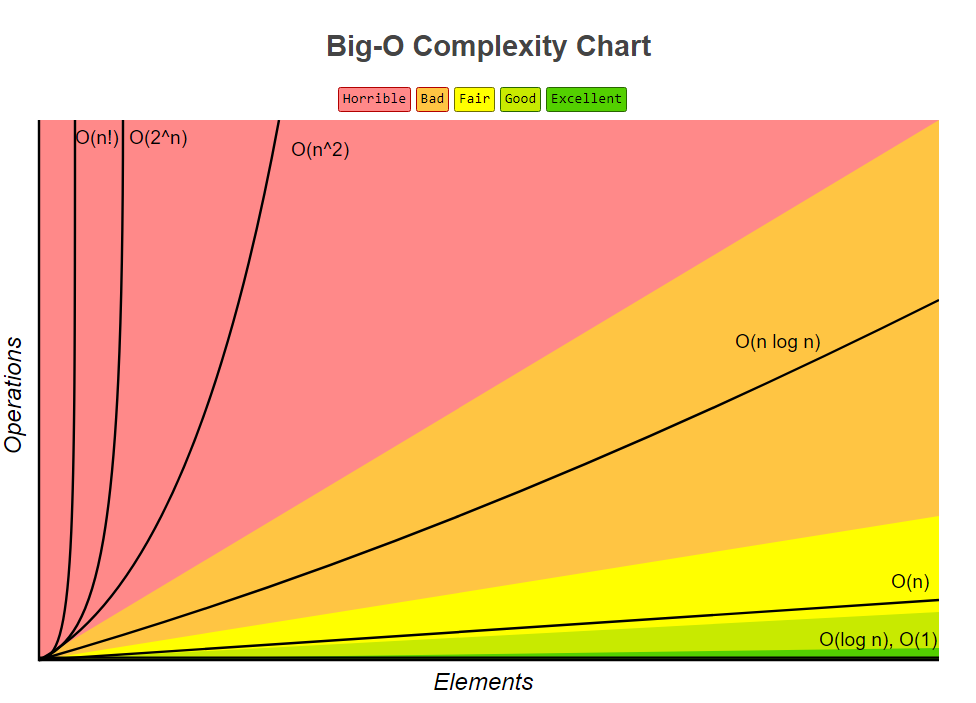
常见时间复杂度对比

image.png

空间复杂度

什么是空间复杂度

  • 算法的存储空间与输入值之间的关系
  • 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做 S(n) = O(f(n))

    大 O 表示法

    S(n) = O(f(n))

常见空间复杂度案例分析

空间复杂度 O(1)

如果算法执行所需要的临时空间不随着某个变量 n 的大小而变化，即此算法空间复杂度为一个常量，可表示为 O(1)

  1. int i = 1;
  2. int j = 2;
  3. ++i;
  4. j++;
  5. int m = i + j;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)

空间复杂度 O(n)

  1. int[] m = new int[n]
  2. for(i=1; i<=n; ++i)
  3. {
  4.    j = i;
  5.    j++;
  6. }

这段代码中，第一行 new 了一个数组出来，这个数据占用的大小为 n，这段代码的2-6行，虽然有循环，但没有再分配新的空间，
因此，这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)

递归中，由于每次递归的数据会保存下来，一般空间复杂度也为 O(n)

常见空间复杂度对比

参考：https://zhuanlan.zhihu.com/p/32326825
https://zhuanlan.zhihu.com/p/50479555
https://www.bigocheatsheet.com/