定义

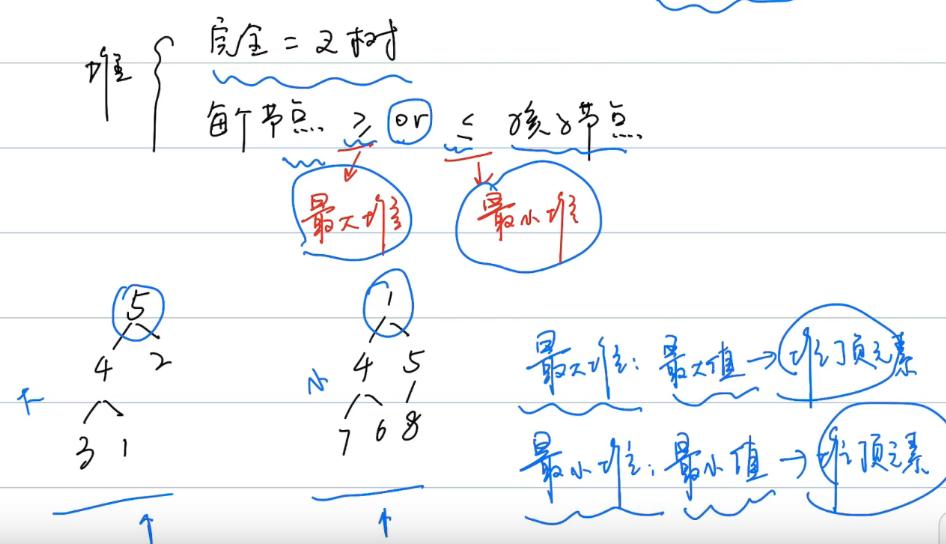
image.png

堆的四种操作

  • 访问 Access ×
  • 搜索 Search 时间复杂度 O(1)
    一般只查看堆顶元素，时间复杂度为 O(1)，查看其他元素为 O(N)
  • 添加 Insert 时间复杂度 O(logN)

只和上一层比较，不需要和同阶层比较

  • 删除 Remove 时间复杂度 O(logN)

由于堆是队列结构，只能从堆中删除堆顶元素。
移除堆顶元素之后，用堆的最后一个节点填补堆顶元素，并将堆的实际元素个数减一；然后将堆自顶向下调整，使其满足最大或最小堆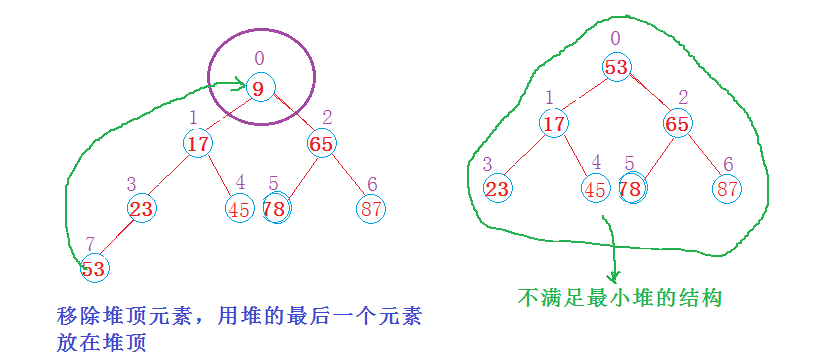
数据结构八：堆 Heap - 图2

堆化操作：时间复杂度O(N)

image.png
时间复杂度解释：https://www.bilibili.com/video/BV1sy4y1q79M?p=39

堆实际的常用操作（Java）

  • 创建堆

    1.       //Create a min heap
    2.       PriorityQueue<Integer> minheap = new PriorityQueue<>();
    3.       //Create a max heap
    4.       PriorityQueue<Integer> maxheap = new PriorityQueue<>(Collections.reverseOrder());

  • 添加元素

    1.       //Add Element
    2.       minheap.add(10);
    3.       minheap.add(8);
    4.       minheap.add(9);
    5.       minheap.add(11);
    6.       minheap.add(2);
    8.       maxheap.add(10);
    9.       maxheap.add(8);
    10.       maxheap.add(9);
    11.       maxheap.add(11);
    12.       maxheap.add(2);
    14.       //[2,8,9,11,10]
    15.       System.out.println(minheap.toString());
    16.       //[11,10,9,8,2]
    17.       System.out.println(maxheap.toString());

  • 获取堆顶元素

    1.       //Peek Element
    2.       minheap.peek();
    3.       maxheap.peek();

  • 删除堆顶元素

    1.       //Delete the top element
    2.       minheap.poll();
    3.       maxheap.poll();

  • 长度

    1.       //Size
    2.       minheap.size();
    3.       maxheap.size();

  • 边删除边遍历

    1.       //Iteration 
    2.       while (!minheap.isEmpty()) {
    3.           System.out.println(minheap.poll());
    4.       }

LeetCode练习

#215

#692

参考：https://www.bilibili.com/read/cv8825697?spm_id_from=333.788.b_636f6d6d656e74.26