时间复杂度
时间复杂度是对一个算法运行时间的度量,通常由一个运行次数最多的基础运算计算获得
空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的度量.通常由存储临时变量的列表来计算获得.
数组
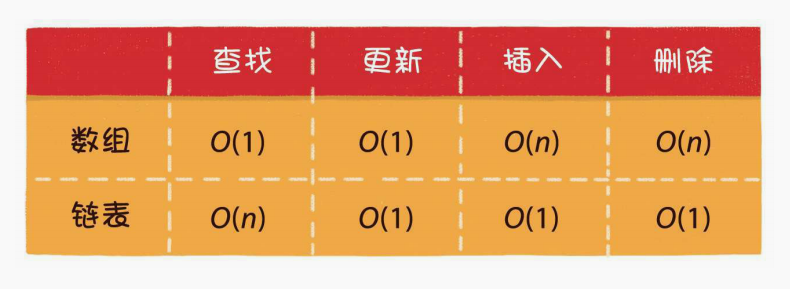
适合读操作多,写操作少的场景
- 数组具有非常高效的随机访问能力,只要给出下标就能用常量时间找到对应元素.
- 数组在插入和删除元素方面都会导致大量元素被迫移动,从而影响效率.
- 如果数组中元素的顺序没有要求,那么在删除元素的时候直接用最后一个元素顶上被删元素的位置.
- 数组基于下标的访问方式可以使用二分查找快速寻找满足条件的值
链表
适合增&删操作多,读操作少的场景
- 除了数据寻找困难一点,增删改都很方便
栈
先进后出的一个线性表
- 可应用在对历史的回溯这一方面,比如浏览器页面访问历史,用户足迹记录
队列
先进先出的一个线性表
数组实现队列可使用循环的方式.
- 队列长度比数组容量少一个,因为队尾永远占一个空的地址空间
- 对首使用一个变量记住,对尾使用一个变量记住,数组容量使用一个变量记住,三个变量结合使用,可以实现一个长度固定的队列
队列一般是用在与顺序相关的应用,讲究先来后到,比如爬虫的爬取顺序,线程访问资源的顺序.
双端队列
结合了栈和队列的特点,既可以先进先出,也可以后进后出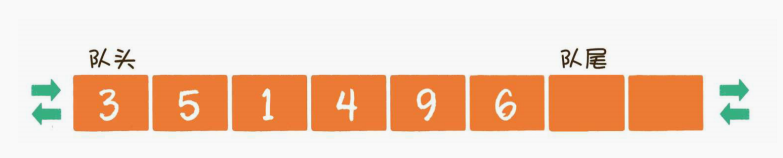
优先队列
谁优先级高谁就先出队列,但这种队列不是基于线性的数据结构,而是基于二叉堆来实现.
二叉树
满二叉树: 除了最后一层的叶子节点,所有的节点都需要满足两个孩子.
完全二叉树: 所有节点的顺序都需要满足满二叉树的节点顺序.
左孩子下标 = 父节点下标2 + 1
右孩子下标 = 父节点下标2 + 2
使用链表实现二叉树,即使用左右两个节点引用即可.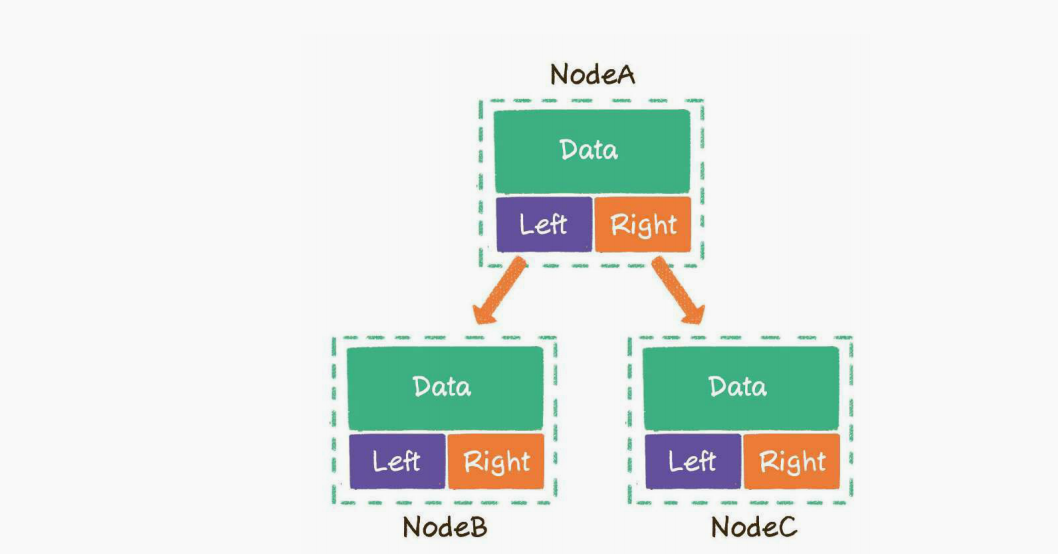
使用数组实现二叉树,那么数组下标代表着节点在二叉树中的顺序.但一个稀疏的二叉树使用数组来存储是很浪费空间的.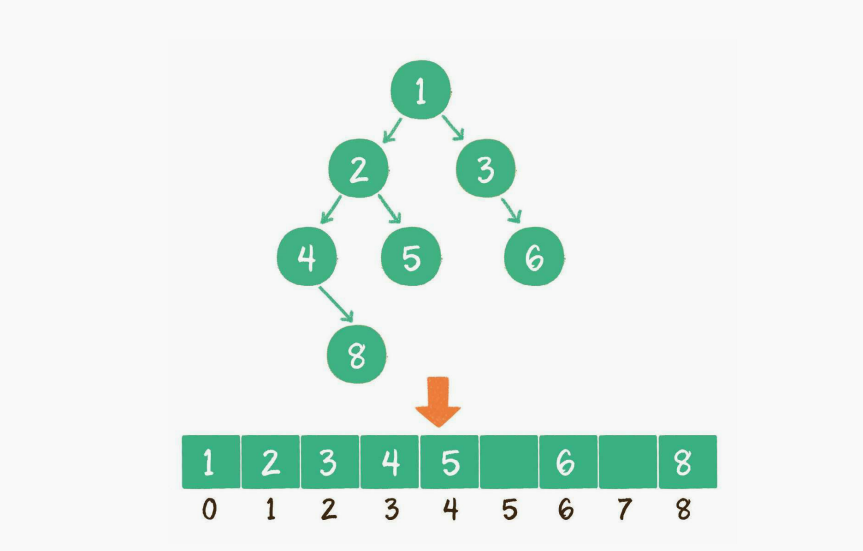
二叉树适合查找相关的场景:
二叉查找树/二叉排序树
有可能会退化成链表,这跟插入的值有关,而且插入已c存在的值似乎不适合.
- 如果左子树不为空,则左子树上所有节点的值均小于根节点的值
- 如果右子树不为空,则右子树上所有节点的值均大于根节点的值
- 左、右子树也都是二叉查找树
二叉堆
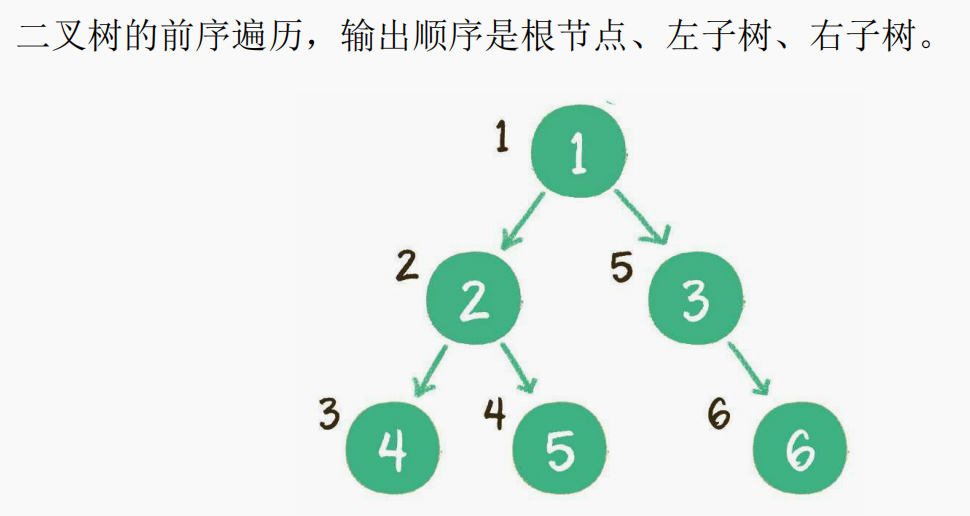
前序遍历(深度遍历)
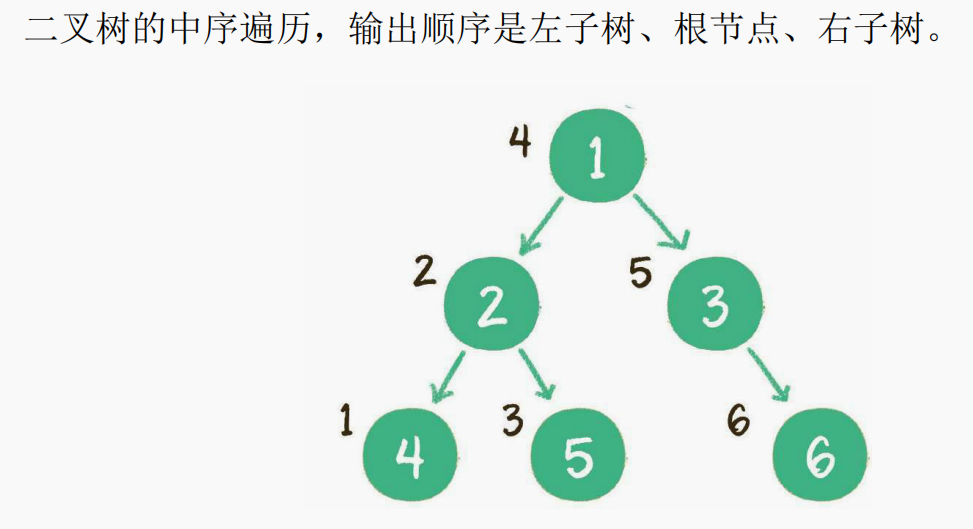
- 中序遍历(深度遍历)
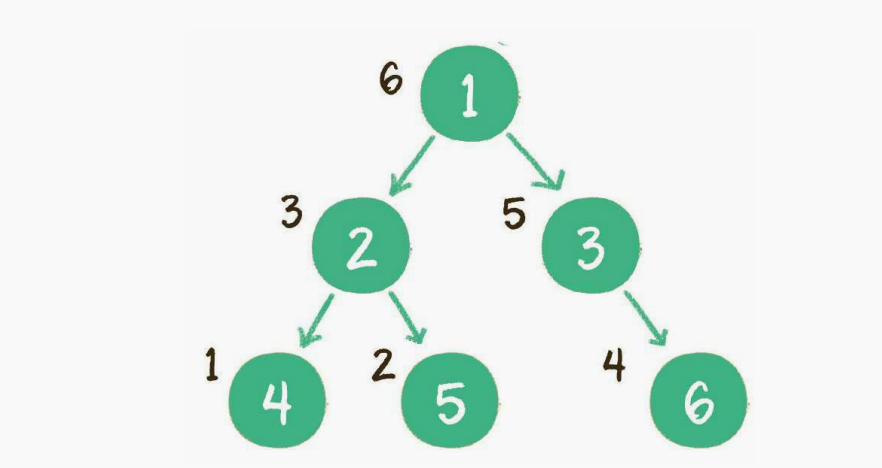
- 后序遍历(深度遍历),左子树&右子树&根节点
- 层序遍历(广度遍历)
最大堆的任何一个父节点的值,都大于或等于它左、右孩子节点的值。
最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值。
如何把一个完全无序的二叉树构建为最大/最小的二叉堆?
- 从最后一个非叶子节点开始,然后开始”下沉”
- 然后在倒数第二个非叶子节点上开始"下沉"
- 倒数第三..
- 倒数第四
- ...一直到第一个节点完毕
插入节点是直接插入到二叉树最后一个可插入的节点中,然后通过二叉树自动调整.
删除节点,是直接使用最后一个节点来替换,然后再在替换的位置上进行调整.

