1.定义

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) 。

2.问题描述

给你两个字符串 text(目标字符串)和 pattern（模式串）请你在text 字符串中找出 pattern 字符串出现的第一个位置（下标从 0 开始）。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/implement-strstr
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

3.思路分析

  • 首先，我认为KMP算法的核心在于next数组，涉及next数组创建以及过程中的回溯问题

两个概念

  • 字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；
  • 字符串的后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

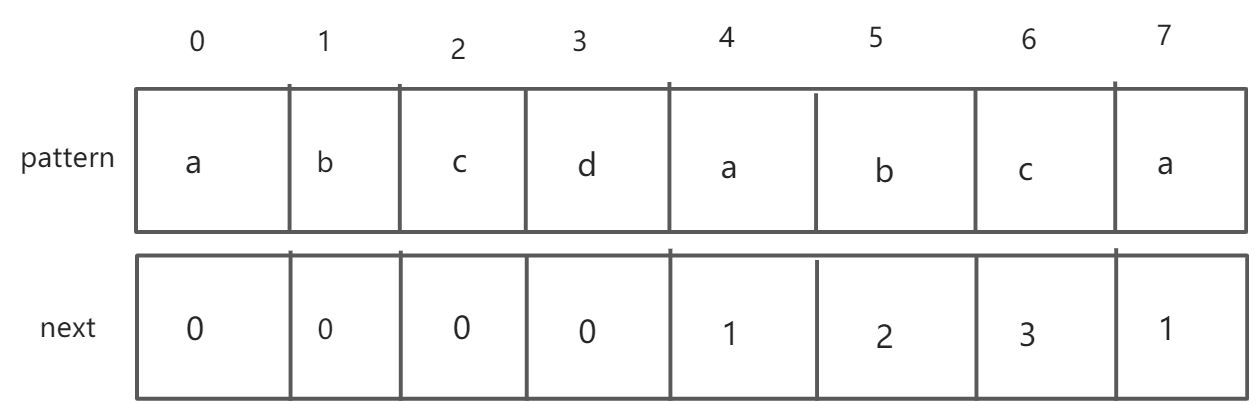
KMP算法 - 图1
显然，next[0]:next数组的第一位永远是0，因为对于”a”本身，并没有 其前缀和后缀
对于next[1]：”ab”的前缀为a,后缀为b，前缀≠后缀，因此next[1]=0；
对于next[2]：”abc”的前缀为”a””ab”,后缀为”c””bc”，前缀≠后缀，因此next[2]=0；
对于next[3]：”abcd”的前缀为”a””ab””abc”,后缀为”d””cd””bcd”，前缀≠后缀，因此next[3]=0；
对于next[4]：”abcda”的前缀为”a””ab””abc””abcd”,后缀为”a””da””cda””bcda”，最大前后缀为”a”，因此next[4]=1；
对于next[5]：”abcdab”的前缀为”a””ab””abc””abcd””abcda”,后缀为”b””ab””dab””cdab””bcdab”，最大前后缀为”ab”，因此next[5]=2；
对于next[6]：”abcdabc”的前缀为”a””ab””abc””abcd””abcda””abcdab”,后缀为”c””bc””abc””dabc””cdabc””bcdabc”，最大前后缀为”abc”，因此next[6]=3；
对于next[7]：next[7]=1；

  1. public static void pattern_next(String pattern, int[] next, int n) { //n表示整个数组的大小
  2.         int left = 0;
  3.         int right = 1;
  4.         next[0] = 0;
  5.         while (right < n) {
  6.             while (left > 0 && pattern.charAt(left) != pattern.charAt(right)) {
  7.                 left = next[left - 1];
  8.             }
  9.             if (pattern.charAt(left) == pattern.charAt(right)) {
  10.                 left++;
  11.             }
  12.             next[right] = left;
  13.             right++;
  14.         }
  15.     }

根据上述代码可知：
当pattern.charAt(left) == pattern.charAt(right)时，我们的left指针向后移1位，对应的 next[right] = left，表示[0,right]中最长相同前后缀是left
当left > 0 && pattern.charAt(left) != pattern.charAt(right)时，我们需要一个回溯操作来确定当前前缀中有无最大相同前后缀，若有则left++，若无则继续回溯，直到left=0；我们唯一容易知道的是：当left和right索引上的内容恰好不同时，此二索引前面的内容是相同的，因为在此之前他们拥有最大相同前后缀

 while (left > 0 && pattern.charAt(left) != pattern.charAt(right)) {
                left = next[left - 1];
            }    //使left等于left-1处对应next数组中的值，此操作为核心要点
  • 解决了next数组的创建以及其内部回溯的问题后，利用next数组进行kmp算法的步骤就容易很多了，kmp算法本质上就是两个数组进行匹配，如果匹配到的某一位上的值不同时，进行回溯，以此来跳过前面不需要进行匹配的内容。

我们再翻回去观察next数组的创建过程，对于pattern中前后两个索引处内容的比较，我们不妨看成是两个pattern字符串进行错位匹配和比较，是不是和kmp算法执行过程如出一辙？下面给出具体代码

4.代码展示

package com.lanqiao01;

import java.lang.reflect.Array;
import java.util.Arrays;

public class KMP {
    public static void main(String[] args) {
        String text = "abxabcabcaby";
        String pattern = "abcaby";
        int n = pattern.length();
        int[] next = new int[n];
        pattern_next(pattern, next, n);     //构造next数组
        //进行字符串的匹配
        for (int i = 0,j = 0; i < text.length(); i++) {

            while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
                j = next[j - 1];
            }
            if (text.charAt(i) == pattern.charAt(j))
                j++;
            if (j == n)
                System.out.println(i - n + 1);
        }
    }


    public static void pattern_next(String pattern, int[] next, int n) {    //n表示整个数组的大小
        int left = 0;
        int right = 1;
        next[0] = 0;
        while (right < n) {
            while (left > 0 && pattern.charAt(left) != pattern.charAt(right)) {
                left = next[left - 1];
            }
            if (pattern.charAt(left) == pattern.charAt(right)) {
                left++;
            }
            next[right] = left;
            right++;
        }
    }
}