1.图论基础
图论在实际笔试中考的不多,但它的经典算法⽐较多,⽐如什么最⼩⽣成树,最短路径,拓扑排序,⼆分图 判定之类的。 <br />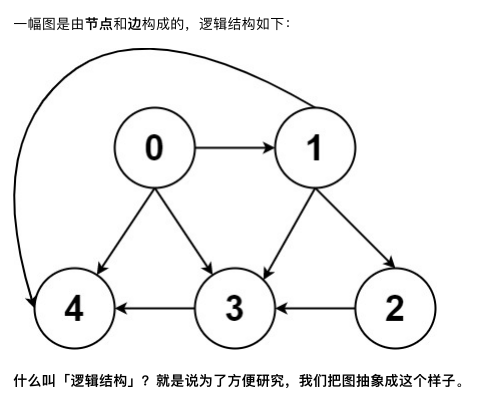<br />在这幅图中,每一个节点都指向了其他的节点,我们称之为**有向图**,边的指向是单向的。
我们通常用邻接表和邻接矩阵来存储图这种结构。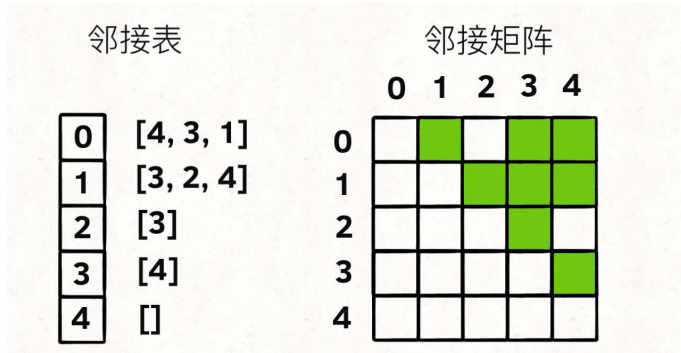
一般做题来说,我们倾向于使用邻接表这种存储方式,可以用map实现,也可以用List实现,只要能够实现如上图中邻接表的对应关系就行。如map就是键值对,List就是list数组中的每个list[i]=new LinkedList();
// 邻接矩阵
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有⼀条指向 y 的边
boolean[][] matrix;
2.Leetcode797.所有可能的路径

题目给了graph数组的定义,graph[1]表示和1相邻的节点的列表,那么我们用dfs深搜,每次搜到一个不重复的就添加进路径列表,直到i==n-1(n为graph的长度),表示已经到达最后一个位置。将路径列表添加进结果列表。
注意,我们的图都是从0开始出发的,所以我们的路径列表先添加1个0
class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<Integer> path=new ArrayList<>();
List<List<Integer>> res=new ArrayList<>();
path.add(0);
dfs(graph,res,path,0);
return res;
}
public void dfs(int[][] graph,List<List<Integer>> res,List<Integer> path,int start){
int n=graph.length;
if(start==n-1){
//path.add(start);
res.add(new ArrayList(path));
return;
}
for(int i:graph[start]){
path.add(i);
dfs(graph,res,path,i);
path.remove(path.size()-1);
}
}
}
3.Leetcode207.课程表
根据题目输入的数组,我们可以画出如下的图: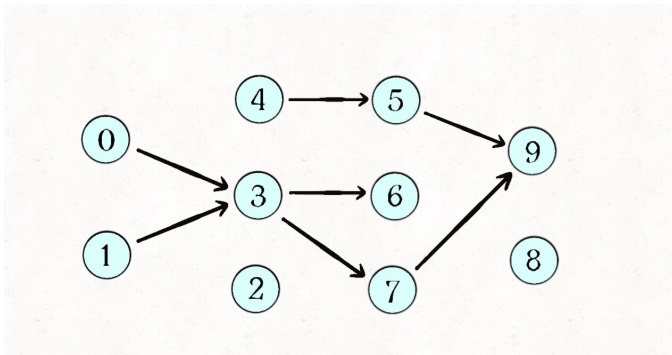
知道了numCourses,相当于我们知道了有多少个节点,那么我们就创建
List
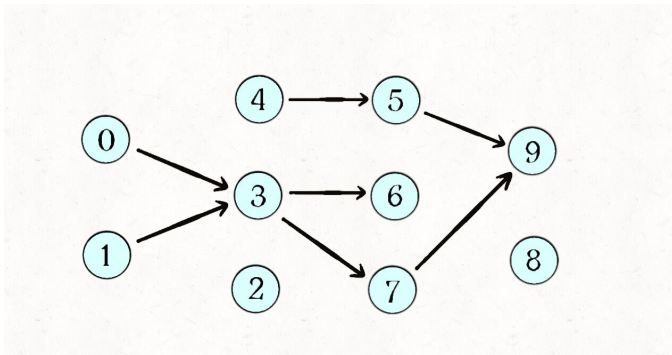
判断我们的这个函数是否能够学完所有的课程,类同于判断一个有向图是否包含环,因为一旦图中有了环,我们dfs的时候如果走到这个节点,就会无休止的在这个环里面走下去,那么我们如何避免dfs走之前再走过的路呢?
很简单,定义一个boolean类型的path数组,遍历过程中,走过了一个节点就把visited设置为true,在dfs函数中开头添加一个判断条件,如果这次深搜的节点已经出现过了,那就不用继续搜索了,说明图中包含环,直接return就完事了。我们还需要定义一个visited数组表示遍历的起点,因为我们不确定从哪个起点开始可以遍历完整张图,所以要全部尝试,同理,我们再dfs之前再次判断visited是否为true,如果是true的话,说明这个起点已经遍历过了,我们直接return 结束遍历就好了。
读者可能会有疑惑:如果出现图中的节点是分离的情况呢?那么无论从哪个节点开始,不是都不能遍历完整个图吗?
我们再仔细的看看题意: ,“可能”,那么结果就一目了然了,就是这么做的。
,“可能”,那么结果就一目了然了,就是这么做的。
class Solution {
boolean hascycle=false;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] subject=new LinkedList[numCourses];
boolean[] path=new boolean[numCourses];
boolean[] visited=new boolean[numCourses];
build(subject,prerequisites,numCourses);
for(int i=0;i<numCourses;i++){
dfs(subject,visited,i,path);
}
return !hascycle;
}
public void build(List<Integer>[] subject,int[][] prerequisites,int numCourses){ //构建邻接表
for(int i=0;i<numCourses;i++){
subject[i]=new LinkedList<Integer>();
}
for(int[] i:prerequisites){
int from=i[1];
int to=i[0];
subject[from].add(to);
}
}
public void dfs(List<Integer>[] subject,boolean[] visited,int start,boolean[] path){
if(path[start]){
hascycle=true;
}
if(hascycle || visited[start]){
return;
}
visited[start]=true;
path[start]=true;
for(int i:subject[start]){
dfs(subject,visited,i,path);
}
path[start]=false;
}
}
4.Leetcode210.课程表Ⅱ

拓扑排序:后续遍历反转之后的结果!!!!!只针对无环有向图,需要进行环检测。
class Solution {
boolean hascycle=false;
List<Integer> res=new LinkedList<>();
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] subject=new LinkedList[numCourses];
boolean[] visited=new boolean[numCourses];
boolean[] path=new boolean[numCourses];
build(subject,prerequisites,numCourses);
for(int i=0;i<numCourses;i++){
dfs(subject,visited,i,path);
}
if(hascycle)return new int[]{};
Collections.reverse(res);
int[] tmp=new int[numCourses];
for(int i=0;i<numCourses;i++){
tmp[i]=res.get(i);
}
return tmp;
}
public void build(List<Integer>[] subject,int[][] prerequisites,int numCourses){ //构建邻接表
for(int i=0;i<numCourses;i++){
subject[i]=new LinkedList<Integer>();
}
for(int[] i:prerequisites){
int from=i[1];
int to=i[0];
subject[from].add(to);
}
}
public void dfs(List<Integer>[] subject,boolean[] visited,int start,boolean[] path){
int n=subject.length;
if(path[start]){
hascycle=true;
}
if(hascycle || visited[start]){
return;
}
visited[start]=true;
path[start]=true;
for(int i:subject[start]){
dfs(subject,visited,i,path);
}
res.add(start);
path[start]=false;
}
}
5.Kruskal算法(克鲁斯卡尔)
1.并查集(Union-find)模板
class UF{
/**
1.构造函数,用于创建联通分量count,parent数组和size数组
2.创建一个方法union用于连接
3.创建一个find方法用于寻找联通分量的根节点
4.创建一个isconnected方法检测两个节点是否连接
5.创建一个count方法,用于返回联通分量的数值
*/
private int count; //联通分量
private int[] parent; //存储一棵树
private int[] size; //记录以下标为根节点的树的重量(节点数)
public UF(int n){
this.count=n;
parent=new int[n];
size=new int[n];
for(int i=0;i<n;i++){
parent[i]=i;
size[i]=1;
}
}
public boolean isconnected(int p,int q){
int rootp=find(p);
int rootq=find(q);
return rootp==rootq;
}
public void union(int p,int q){
int rootp=find(p);
int rootq=find(q);
if(rootp==rootq){
return;
}
if(size[rootp]>size[rootq]){
parent[rootq]=rootp;
size[rootp]+=size[rootq];
}else{
parent[rootp]=rootq;
size[rootq]+=size[rootp];
}
count--;
}
public int find(int x){
while(parent[x]!=x){
parent[x]=parent[parent[x]]; //可加可不加,用于进行路径压缩,减少时间复杂度
x=parent[x];
}
return x;
}
public int count(){
return count;
}
}
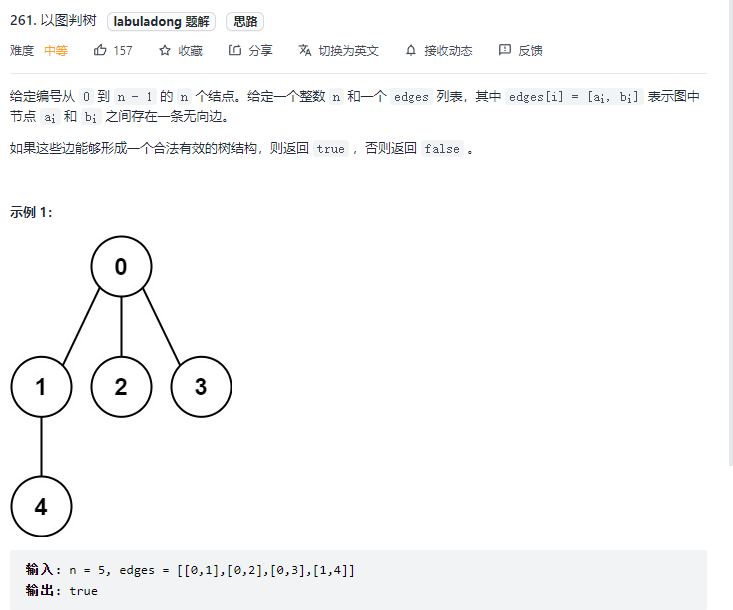
2.1Leetcode.261以图判树
class Solution {
public boolean validTree(int n, int[][] edges) {
UF uf=new UF(n);
for(int[] edge:edges){
int p=edge[0];
int q=edge[1];
if(uf.isconnected(p,q)){
return false;
}
uf.union(p,q);
}
return uf.count()==1;
}
}
class UF{
/**
1.构造函数,用于创建联通分量count,parent数组和size数组
2.创建一个方法union用于连接
3.创建一个find方法用于寻找联通分量的根节点
4.创建一个isconnected方法检测两个节点是否连接
5.创建一个count方法,用于返回联通分量的数值
*/
private int count;
private int[] size;
private int[] parent;
public UF(int n){
this.count=n;
parent=new int[n];
size=new int[n];
for(int i=0;i<n;i++){
parent[i]=i;
size[i]=1;
}
}
public void union(int p,int q){
int rootp=find(p);
int rootq=find(q);
if(rootp==rootq){
return;
}else{
if(size[rootp]>size[rootq]){
parent[rootq]=rootp;
size[rootp]+=size[rootq];
}else{
parent[rootp]=rootq;
size[rootq]+=size[rootp];
}
}
count--;
}
public boolean isconnected(int p ,int q){
int rootp=find(p);
int rootq=find(q);
return rootp==rootq;
}
public int find(int x){
while(parent[x]!=x){
parent[x]=parent[parent[x]];
x=parent[x];
}
return x;
}
public int count(){
return count;
}
}
2.最小生成树问题
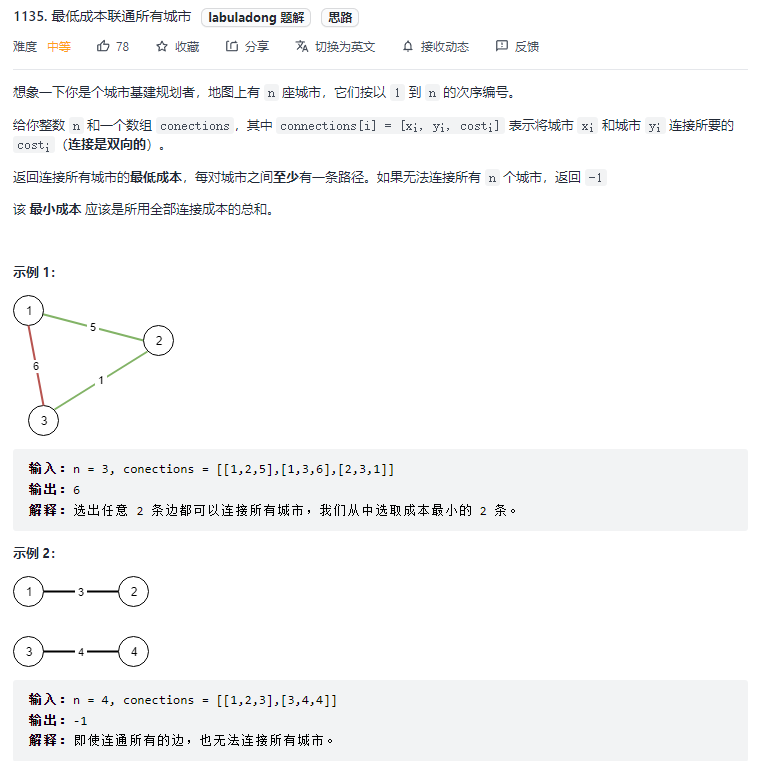
Leetcode1135.最低成本联通所有城市
class Solution {
public int minimumCost(int n, int[][] connections) {
int min=0;
UF uf=new UF(n+1);
Arrays.sort(connections,(a,b)->(a[2]-b[2]));
for(int[] edge:connections){
int p=edge[0];
int q=edge[1];
int weight=edge[2];
if(uf.isconnected(p,q)){
continue;
}
min+=weight;
uf.union(p,q);
}
return uf.count()==2?min:-1;
}
}
class UF{
/**
1.构造函数,用于创建联通分量count,parent数组和size数组
2.创建一个方法union用于连接
3.创建一个find方法用于寻找联通分量的根节点
*/
private int count; //联通分量
private int[] parent; //存储一棵树
private int[] size; //记录以下标为根节点的树的重量(节点数)
public UF(int n){
this.count=n;
parent=new int[n];
size=new int[n];
for(int i=0;i<n;i++){
parent[i]=i;
size[i]=1;
}
}
public boolean isconnected(int p,int q){
int rootp=find(p);
int rootq=find(q);
return rootp==rootq;
}
public void union(int p,int q){
int rootp=find(p);
int rootq=find(q);
if(rootp==rootq){
return;
}
if(size[rootp]>size[rootq]){
parent[rootq]=rootp;
size[rootp]+=size[rootq];
}else{
parent[rootp]=rootq;
size[rootq]+=size[rootp];
}
count--;
}
public int find(int x){
while(parent[x]!=x){
parent[x]=parent[parent[x]]; //可加可不加,用于进行路径压缩,减少时间复杂度
x=parent[x];
}
return x;
}
public int count(){
return count;
}
}
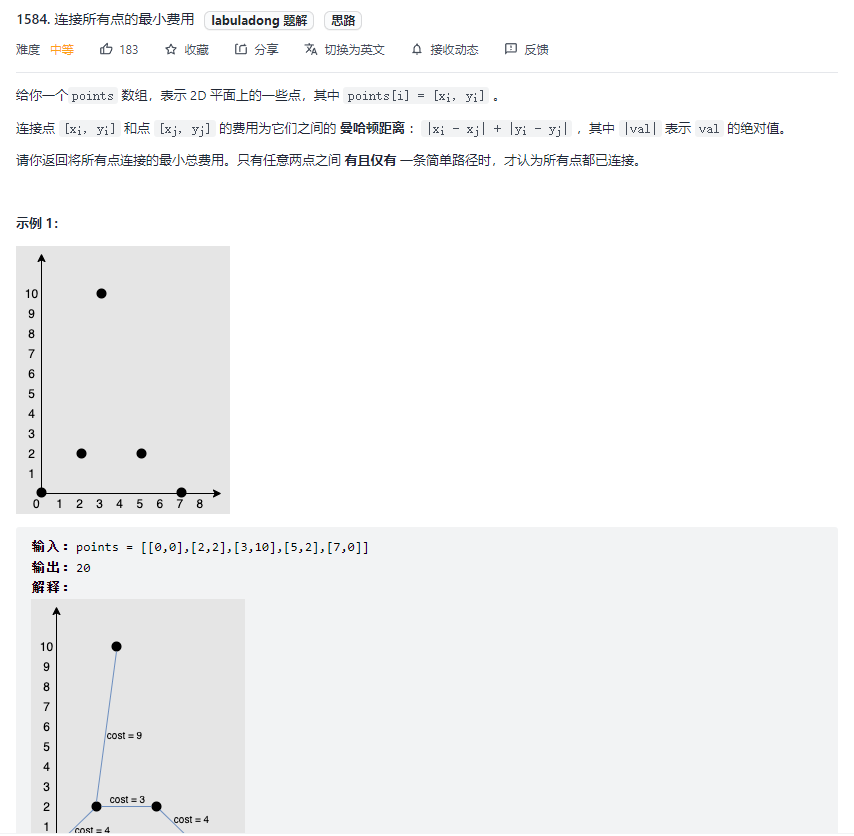
Leetcode.1584连接所有点的最小费用
class Solution {
public int minCostConnectPoints(int[][] points) {
int n=points.length;
int length=0;
UF uf=new UF(n);
List<int[]> edges=new ArrayList<>();
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
int xi=points[i][0];
int yi=points[i][1];
int xj=points[j][0];
int yj=points[j][1];
edges.add(new int[]{i,j,Math.abs(xi-xj)+Math.abs(yi-yj)});
}
}
Collections.sort(edges,(a,b)->(a[2]-b[2]));
for(int[] edge:edges){
int p=edge[0];
int q=edge[1];
int weight=edge[2];
if(uf.isconnected(p,q)){
continue;
}else{
length+=weight;
uf.union(p,q);
}
}
return length;
}
}
class UF{
private int count;
private int[] size;
private int[] parent;
public UF(int n){
this.count=n;
size=new int[n];
parent=new int[n];
for(int i=0;i<n;i++){
parent[i]=i;
size[i]=1;
}
}
public boolean isconnected(int p,int q){
int rootp=find(p);
int rootq=find(q);
return rootp==rootq;
}
public int find(int x){
while(parent[x]!=x){
parent[x]=parent[parent[x]];
x=parent[x];
}
return x;
}
public void union(int p,int q){
int rootp=find(p);
int rootq=find(q);
if(isconnected(p,q)){
return;
}else{
if(size[rootp]>size[rootq]){
parent[rootq]=rootp;
size[rootp]+=size[rootq];
}else{
parent[rootp]=rootq;
size[rootq]+=size[rootp];
}
count--;
}
}
}
6.Dijkstra算法(迪杰斯特拉算法)
1.算法模板
// 返回节点 from 到节点 to 之间的边的权重
int weight(int from, int to);
// 输入节点 s 返回 s 的相邻节点
List<Integer> adj(int s);
// 输入一幅图和一个起点 start,计算 start 到其他节点的最短距离
int[] dijkstra(int start, List<Integer>[] graph) {
// 图中节点的个数
int V = graph.length;
// 记录最短路径的权重,你可以理解为 dp table
// 定义:distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
int[] distTo = new int[V];
// 求最小值,所以 dp table 初始化为正无穷
Arrays.fill(distTo, Integer.MAX_VALUE);
// base case,start 到 start 的最短距离就是 0
distTo[start] = 0;
// 优先级队列,distFromStart 较小的排在前面
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distFromStart - b.distFromStart;
});
// 从起点 start 开始进行 BFS
pq.offer(new State(start, 0));
while (!pq.isEmpty()) {
State curState = pq.poll();
int curNodeID = curState.id;
int curDistFromStart = curState.distFromStart;
if (curDistFromStart > distTo[curNodeID]) {
// 已经有一条更短的路径到达 curNode 节点了
continue;
}
// 将 curNode 的相邻节点装入队列
for (int nextNodeID : (curNodeID)) {
// 看看从 curNode 达到 nextNode 的距离是否会更短
int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
if (distTo[nextNodeID] > distToNextNode) {
// 更新 dp table
distTo[nextNodeID] = distToNextNode;
// 将这个节点以及距离放入队列
pq.offer(new State(nextNodeID, distToNextNode));
}
}
}
return distTo;
}
class State {
// 图节点的 id
int id;
// 从 start 节点到当前节点的距离
int distFromStart;
State(int id, int distFromStart) {
this.id = id;
this.distFromStart = distFromStart;
}
}
2.最短路径问题
Leetcode.743网络延迟时间

分析:我们通常用dijkstra算法来求最短路径的问题,前提是:抽象化的图不是负权图(该算法无法求负权图的最短路径;对于该题:我们根据题意构造一个有关图的邻接表,因为有n个网络节点,并且序号从1开始,所以我们构建的临界表的数组长度为n+1:List<int[]>[] graph=new LinkedList[n+1];
我们邻接表中的数据首先必须要有当前节点的邻居节点,又因为求最短路径,所以邻接表中还应该存储当前节点到邻居节点的权值,因此我们的graph[]中存储的应该是以int【目标邻居节点,权值】为单位的元素,为了方便我们对数据进行存取,我们用LinkedList<>实现我们graph数组的每一行数据:
for(int i=1;i<graph.length;i++){
graph[i]=new LinkedList<int[]>();
}
遍历一遍初始times[ ][ ]数组,将对应的元素添加进graph[ ]数组中:
for(int[] edge:times){
int from=edge[0];
int to=edge[1];
int weight=edge[2];
graph[from].add(new int[]{to,weight});
}
根据题意,我们用优先队列实现dijkstra算法,首先要明确,这个算法需要什么参数:
1.起始点
2.一幅图(邻接表)
我们上面创建的邻接表就可以在这里发挥作用了
为什么要用优先队列,想象图为一个多叉树,我们把根节点的邻居节点加入到队列中,但是我们无法确定根节点到每个邻居节点的大小,所以我们利用优先队列按照升序排序,这样每次poll()的时候我们都能拿到理想的“潜力”最大的元素(更有可能接近最短路径的元素)
初始distTo【】数组(存储start到目标点的最短路径长度)每个元素设置为Integer.MAX_VALUE。
根据定义,start到start的权值为0(距离为0),所以distTo【start】=0;
每次poll()一个元素,我们记录他的id和起始点到该点的距离
int[] distTo=new int[graph.length]; //从start到当前节点的距离
Arrays.fill(distTo,Integer.MAX_VALUE);
distTo[start]=0; //start到start的距离为0
pq.add(new State(start,0));
while(!pq.isEmpty()){
State curState=pq.poll();
int curNodeId=curState.id;
int curdisFromStart=curState.disFromStart;
if(curdisFromStart>distTo[curNodeId]){
// 已经有⼀条更短的路径到达 curNodeId 节点了
continue;
}
如果检测到有更短的路径,那么提取graph[curNodeId]中的元素,找到当前最短路径+到下一个节点的权值=最小的数值,更新distTo【】数组
for(int[] neighbor:graph[curNodeId]){
int nextNodeid=neighbor[0];
int nextdistTo=neighbor[1]+distTo[curNodeId];
if(distTo[nextNodeid]>nextdistTo){
distTo[nextNodeid]=nextdistTo;
pq.add(new State(nextNodeid,nextdistTo));
}
}
所有的元素遍历完后,生成distTo【】数组,返回。
最后只要遍历distTo【】数组,如果有一个数=Integer.MAX_VALUE则说明有一个节点没有达到,则return-1;
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
List<int[]>[] graph=new LinkedList[n+1];
for(int i=1;i<graph.length;i++){
graph[i]=new LinkedList<int[]>();
}
for(int[] edge:times){
int from=edge[0];
int to=edge[1];
int weight=edge[2];
graph[from].add(new int[]{to,weight});
}
int res=0;
int distTo[]=dijkstra(k,graph);
for(int i=1;i<graph.length;i++){
if(distTo[i]==Integer.MAX_VALUE){
return -1;
}
res=Math.max(res,distTo[i]);
}
return res;
}
public int[] dijkstra(int start,List<int[]>[] graph){
int[] distTo=new int[graph.length]; //从start到当前节点的距离
Arrays.fill(distTo,Integer.MAX_VALUE);
Queue<State> pq=new PriorityQueue<>((a,b)->{
return a.disFromStart-b.disFromStart;
});
distTo[start]=0; //start到start的距离为0
pq.add(new State(start,0));
while(!pq.isEmpty()){
State curState=pq.poll();
int curNodeId=curState.id;
int curdisFromStart=curState.disFromStart;
if(curdisFromStart>distTo[curNodeId]){
continue;
}
for(int[] neighbor:graph[curNodeId]){
int nextNodeid=neighbor[0];
int nextdistTo=neighbor[1]+distTo[curNodeId];
if(distTo[nextNodeid]>nextdistTo){
distTo[nextNodeid]=nextdistTo;
pq.add(new State(nextNodeid,nextdistTo));
}
}
}
return distTo;
}
}
class State{
int disFromStart;
int id;
public State(int id,int disFromStart){
this.id=id;
this.disFromStart=disFromStart;
}
}
蓝桥杯2021省赛:路径

标准的最短路问题,主要细节就是:结合了数论最大公约数和最小公倍数的求法,其他的就套dijkstra模板就好了
最大公约数与最小公倍数
public static int gcd(int m, int n) { // 最大公约数 if (m % n == 0) return n; return gcd(n, m % n); } public static int lcm(int m, int n) { // 最小公倍数 return m * n / gcd(m, n); }```java package lanqiao;
import java.util.Arrays; import java.util.LinkedList; import java.util.List; import java.util.PriorityQueue; import java.util.Queue;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
// 构建邻接表
List<int[]>[] graph = new LinkedList[2022];
for (int i = 0; i < graph.length; i++) {
graph[i] = new LinkedList<int[]>();
}
for (int i = 1; i <= 2021; i++) {
for (int j = 1; j <= 2021; j++) {
if (i == j) {
continue;
} else if (Math.abs(i - j) > 21) {
continue;
} else if (Math.abs(i - j) <= 21) {
graph[i].add(new int[] { j, lcm(i, j) });
}
}
}
int[] disTo = dijkstra(graph, 1);
System.out.println(disTo[2021]);
}
public static int[] dijkstra(List<int[]>[] graph, int start) {
int[] disTostart = new int[graph.length];
Queue<State> q = new PriorityQueue<State>((a, b) -> {
return a.disFromstart - b.disFromstart;
});
Arrays.fill(disTostart, Integer.MAX_VALUE);
disTostart[start] = 0;
q.add(new State(start, 0));
while (!q.isEmpty()) {
State curNode = q.poll();
int curId = curNode.id;
int curdisFromstart = curNode.disFromstart;
if (curdisFromstart > disTostart[curId]) {
continue;
}
for (int[] neighbor : graph[curId]) {
int nextNodeid = neighbor[0];
int nextNodedis = disTostart[curId] + neighbor[1];
if (nextNodedis < disTostart[nextNodeid]) {
disTostart[nextNodeid] = nextNodedis;
q.add(new State(nextNodeid, nextNodedis));
}
}
}
return disTostart;
}
public static int gcd(int m, int n) { // 最大公约数
if (m % n == 0)
return n;
return gcd(n, m % n);
}
public static int lcm(int m, int n) { // 最小公倍数
return m * n / gcd(m, n);
}
}
class State { int id; int disFromstart;
public State(int id, int disFromstart) {
this.id = id;
this.disFromstart = disFromstart;
}
}
<a name="tX3J8"></a>
# 7.Floyd算法(动态规划思想)
<a name="VVew6"></a>
## 1.算法模板:
```java
public class FloydAlgorithm {
public static int MaxValue = 100000;
public static int[][] path;
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.println("请输入顶点数和边数:");
//顶点数
int vertex = input.nextInt();
//边数
int edge = input.nextInt();
int[][] matrix = new int[vertex][vertex];
//初始化邻接矩阵
for (int i = 0; i < vertex; i++) {
for (int j = 0; j < vertex; j++) {
matrix[i][j] = MaxValue;
}
}
//初始化路径数组
path = new int[matrix.length][matrix.length];
//初始化边权值
for (int i = 0; i < edge; i++) {
System.out.println("请输入第" + (i + 1) + "条边与其权值:");
int source = input.nextInt();
int target = input.nextInt();
int weight = input.nextInt();
matrix[source][target] = weight;
}
//调用算法计算最短路径
floyd(matrix);
}
//非递归实现
public static void floyd(int[][] matrix) {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
path[i][j] = -1;
}
}
for (int m = 0; m < matrix.length; m++) {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
if (matrix[i][m] + matrix[m][j] < matrix[i][j]) {
matrix[i][j] = matrix[i][m] + matrix[m][j];
//记录经由哪个点到达
path[i][j] = m;
}
}
}
}
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
if (i != j) {
if (matrix[i][j] == MaxValue) {
System.out.println(i + "到" + j + "不可达");
} else {
System.out.print(i + "到" + j + "的最短路径长度是:" + matrix[i][j]);
System.out.print("最短路径为:" + i + "->");
findPath(i, j);
System.out.println(j);
}
}
}
}
}
//递归寻找路径
public static void findPath(int i, int j) {
int m = path[i][j];
if (m == -1) {
return;
}
findPath(i, m);
System.out.print(m + "->");
findPath(m, j);
}
}
2.蓝桥杯2021省赛:路径

package lanqiao;
import java.util.Arrays;
import java.util.Scanner;
/**
* 小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图 中的最短路径。
*
* 小蓝的图由 2021 个结点组成,依次编号 1 至 2021。
*
* 对于两个不同的结点 a, b,如果 a 和 b 的差的绝对值大于 21,则两个结点 之间没有边相连;如果 a 和 b 的差的绝对值小于等于
* 21,则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。
*
* 例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无 向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为
* 75。
*
* 请计算,结点 1 和结点 2021 之间的最短路径长度是多少。
*
* 提示:建议使用计算机编程解决问题。
*
* @author luzhendong
*
*/
public class Floyd {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();// 节点个数
// int bian = sc.nextInt();// 边的个数
int[][] matrix = new int[N + 1][N + 1];
int[][] path = new int[N + 1][N + 1];
// for (int i = 0; i < matrix.length; i++) {
// Arrays.fill(matrix[i], Integer.MAX_VALUE);
// }
// for (int i = 0; i < bian; i++) {
// System.out.println("请输入第" + (i + 1) + "条边与其权值:");
// int source = sc.nextInt();
// int target = sc.nextInt();
// int weight = sc.nextInt();
// matrix[source][target] = weight;
// }
for (int i = 0; i <= N; i++) {
for (int j = i + 1; j <= N; j++) {
if (Math.abs(i - j) <= 21) {
matrix[i][j] = lcm(i, j);
matrix[j][i] = lcm(i, j);
}
}
}
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
if (matrix[i][j] == 0) {
matrix[i][j] = 1000000000;
}
}
}
// for (int i = 0; i < matrix.length; i++) {
// for (int j = 0; j < matrix[0].length; j++) {
// System.out.print(matrix[i][j] + " ");
// }
// System.out.println();
// }
for (int j = 0; j < path.length; j++) {
Arrays.fill(path[j], -1);
}
for (int k = 0; k < matrix.length; k++) {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
if ((matrix[i][k] + matrix[k][j]) < matrix[i][j]) {
matrix[i][j] = matrix[i][k] + matrix[k][j];
path[i][j] = k;
}
}
}
}
System.out.println(matrix[1][2021]);//10266837
}
public static int gcd(int m, int n) {
if (m % n == 0)
return n;
return gcd(n, m % n);
}
public static int lcm(int m, int n) {
return m * n / gcd(m, n);
}
}
8.蓝桥杯:迷宫(BFS)

- 输入:
01010101001011001001010110010110100100001000101010 00001000100000101010010000100000001001100110100101 01111011010010001000001101001011100011000000010000 01000000001010100011010000101000001010101011001011 00011111000000101000010010100010100000101100000000 11001000110101000010101100011010011010101011110111 00011011010101001001001010000001000101001110000000 10100000101000100110101010111110011000010000111010 00111000001010100001100010000001000101001100001001 11000110100001110010001001010101010101010001101000 00010000100100000101001010101110100010101010000101 11100100101001001000010000010101010100100100010100 00000010000000101011001111010001100000101010100011 10101010011100001000011000010110011110110100001000 10101010100001101010100101000010100000111011101001 10000000101100010000101100101101001011100000000100 10101001000000010100100001000100000100011110101001 00101001010101101001010100011010101101110000110101 11001010000100001100000010100101000001000111000010 00001000110000110101101000000100101001001000011101 10100101000101000000001110110010110101101010100001 00101000010000110101010000100010001001000100010101 10100001000110010001000010101001010101011111010010 00000100101000000110010100101001000001000000000010 11010000001001110111001001000011101001011011101000 00000110100010001000100000001000011101000000110011 10101000101000100010001111100010101001010000001000 10000010100101001010110000000100101010001011101000 00111100001000010000000110111000000001000000001011 10000001100111010111010001000110111010101101111000
- 输出
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDR
1.思路分析
迷宫问题找最短路,首先应该想到的是BFS算法,核心思想就是在图中找到具体的路径,套用BFS算法框架就可以。需要注意的是:题目要求我们输出步数最小的前提下字典序最小的答案。因此我们对起点进行移动的时候优先级——> D-L-R-U
2.代码
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
char[][] arr=new char[30][50];
for(int i=0;i<30;i++){
arr[i]=sc.nextLine().toCharArray();
}
int[][] dis={
{1,0},
{0,-1},
{0,1},
{-1,0}
};
String[] s={"D","L","R","U"};
Queue<Node> q=new LinkedList<>();
q.offer(new Node(0,0,""));
arr[0][0]='1';
String res="";
while(!q.isEmpty()){
Node cur=q.poll();
if(cur.x==29&&cur.y==49){
res=cur.s;
break;
}
for(int i=0;i< dis.length;i++){
int x=cur.x+dis[i][0];
int y=cur.y+dis[i][1];
String curstr= cur.s+s[i];
if(x>=0&&x<30&&y>=0&&y<50&&arr[x][y]=='0'){
q.offer(new Node(x,y,curstr));
arr[x][y]='1';
}
}
}
System.out.println(res);
}
public static class Node{
int x;
int y;
String s;
public Node(int x, int y, String s) {
this.x = x;
this.y = y;
this.s = s;
}
}
}