1.问题描述

设计一个算法，求7的十次方（要求效率尽可能的快）

2.思路分析

最朴素的算法，就是用10个7相乘，7×7×7×7×7×7×7×7×7×7就是答案，但是观察这个式子，我们可以看出总共进行了9次乘法，对于此题，计算机可以很快的求出答案，但是如果我们的数据量很大呢，幂指数增加的时候，我们的结果也在成指数级的增大，最终会导致超出当前数据结构所能存储的最大值，爆long long。
因为我们乘法的运算过程是相同的，在这样一个情况下，我们怎么样去提高运算效率？答案就是：减少乘法运算的次数。
- 先算7的5次方：7×7×7×7×7=7^5,再算（7^5）^2，结果就是我们要求的答案，那么这个算式总共进行了5次乘法，这个式子还能进行拆分
- 先算7×7=49，再算（7^2）^2×7（7的5次方），再次对这个式子平方就求得了7的十次方，这个算是总共进行了4次乘法。

模仿这个拆分的过程，我们可以得出一个在O(logn)时间复杂度的算法

2.2递归快速幂

计算A的n次方，当n为偶数，我们计算A的二分之n次方再平方
当n为奇数，我们计算A的n-1次方（这样，n-1为偶数，我们又可以愉快的递归下去了！！！）
直到n=0时，结果为1，这个就是递归出口。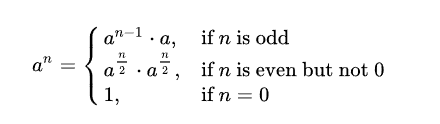

public static int quickPower(int A,int n){
    if(n==0)
        return 1;
    else if (n%2==1)
        return quickPower(A,n-1)*A;
    else {
        int temp=quickPower(A,n/2);
        return temp*temp;
    }
}

2.3二进制快速幂

7的10次方，我们引入二进制，对于10的二进制为1010，我们不断的把二进制&1，然后>>1位，就可以轻松的将每一位上的数字与1相&
当&1以后仍为1，则乘上这个数对应的权值，刚开始权值为2的0次，然后是2的平方，然后是2的四次方……即8，4，2，1，可见我们的权值总是在前面的基础上进行平方，因此二进制快速幂的整体思路就是设置一个ans初始值为1（ans最后的数值就是我们要求的结果），我们不断的把n&1，遇到结果为1的就乘上A，然后n左移1位，权值平方a×a。

public static int quickPower(int A,int n){
    int ans=1;
    while (n!=0){
        if ((n&1)==1){
            ans=ans*A;
        }
        n=n>>1;
        A=A*A;
    }
    return ans;
}

3.拓展——矩阵快速幂

矩阵快速幂，顾名思义就是利用矩阵进行快速幂运算。和普通快速幂唯一的区别就是：矩阵快速幂利用了矩阵的乘法（线性代数）。该方法常与递推公式结合使用
矩阵的乘法：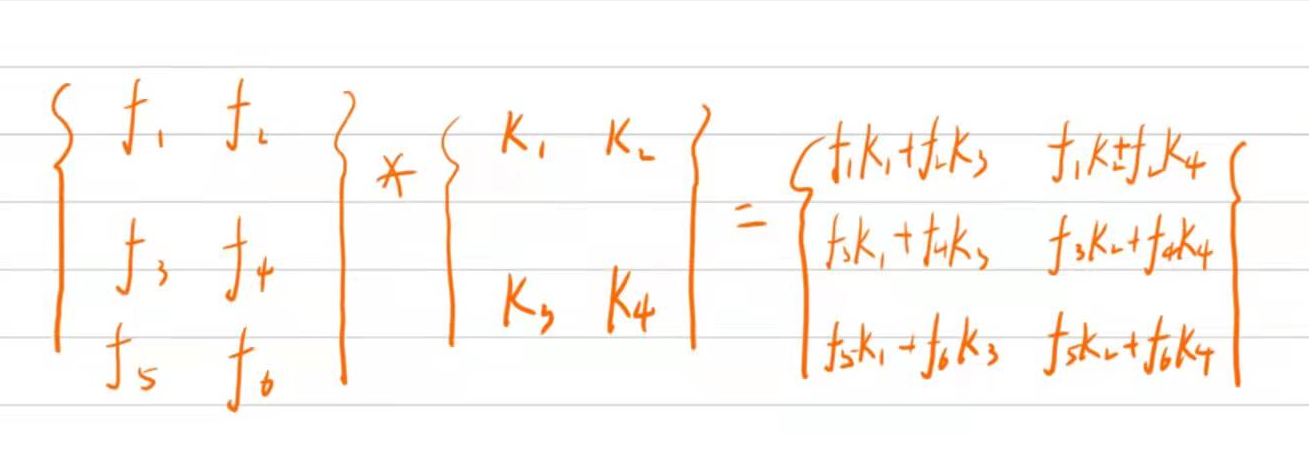

开个玩笑：知道矩阵的乘法后，你就入门线性代数了

模板

//矩阵乘法运算
public static int[][] matrixMultiply(int[][] A, int[][] B) {
 int[][] C = new int[A.length][B[0].length];    //用于储存矩阵乘法后的结果
 //Arrays.fill(C, 0);
 for (int i = 0; i < A.length; i++) {
     for (int j = 0; j < B[0].length; j++) {
         for (int k = 0; k < B[0].length; k++) {
             C[i][j] += A[i][k] * B[k][j];
         }
     }
 }
      return C;
}

  private static int[][] quickPower(int[][] C, int n) { //n表示幂
      /*先构建单位矩阵，其作用相当于普通快速幂运算当中的ans=1初始值，单位
      矩阵乘以任何矩阵都等于本身
      */
      int[][] ans = new int[C.length][C[0].length];
      for (int i = 0; i < ans.length; i++) {
          ans[i][i] = 1;
      }
      /*
      进行快速幂运算
       */
      while (n != 0) {
          if ((n & 1) == 1) {
              ans = matrixMultiply(ans, C);
          }
          C = matrixMultiply(C, C);
          n = n >> 1;
      }
      return ans;
  }

4.例题：矩阵快速幂求斐波那契数列

这是一个典型的利用矩阵快速幂对斐波那契数列进行求解的问题，知道递推公式后，我们首先要明确A×B=C中的B是什么，推理过程如下：

代码如下： ```java package com.lanqiao01; import java.util.Scanner;

public class 矩阵快速幂 { public static void main(String[] args) { int[][] A={ {1,1}, {1,0} }; int[][] B={ {1,1}, {0,0} }; Scanner sc=new Scanner(System.in); int i = sc.nextInt(); if(i==1 ||i==2){ System.out.println(1); } int[][] Z=matrixMultiply(B,quickPower(A,i-2)); System.out.println(Z[0][0]); } //1 1 2 3 5 8 13 21 //矩阵乘法运算 public static int[][] matrixMultiply(int[][] A, int[][] B) { int[][] C = new int[A.length][B[0].length]; //Arrays.fill(C, 0); for (int i = 0; i < A.length; i++) { for (int j = 0; j < B[0].length; j++) { for (int k = 0; k < B[0].length; k++) { C[i][j] += A[i][k] * B[k][j]; } } } return C; }

//快速幂运算
private static int[][] quickPower(int[][] C, int n) { //n表示幂
    /*先构建单位矩阵，其作用相当于普通快速幂运算当中的ans=1初始值，单位
    矩阵乘以任何矩阵都等于本身
    */
    int[][] ans = new int[C.length][C[0].length];
    for (int i = 0; i < ans.length; i++) {
        ans[i][i] = 1;
    }
    /*
    进行快速幂运算
     */
    while (n != 0) {
        if ((n & 1) == 1) {
            ans = matrixMultiply(ans, C);
        }
        C = matrixMultiply(C, C);
        n = n >> 1;
    }
    return ans;
}

}

```

5.视频链接

https://www.bilibili.com/video/BV1Q4411U7cC?p=2&share_source=copy_web
https://www.bilibili.com/video/BV1FZ4y1F7AJ?share_source=copy_web

算法入门

数论基础——快速幂