首先说明一下为什么把回溯算法和dfs算法(深度优先搜索)放在一块,笔者的算法学习道路受博主labuladong的影响较深,在学习此算法的同时认为dfs和回溯在本质上并无区别,相比于将两个算法区分开来,我更愿意称回溯是dfs中可选择的一种操作,在解决有关树和图的问题时,我们更愿意称之为dfs算法。
框架:
result = []def backtrack(路径, 选择列表): //路径:记录已做出的选择 选择列表:可供选择的道路if 满⾜结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择
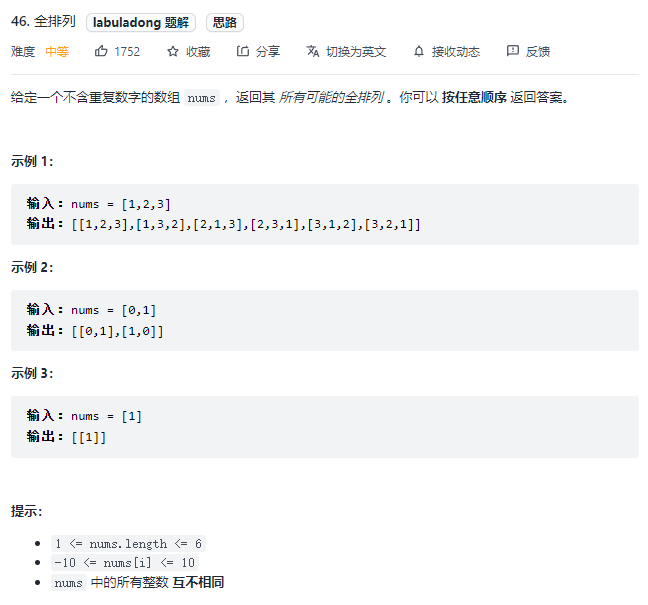
1.Leetcode.46全排列
1.1思路分析
全排列问题非常的常见,相信大家在初中的数学中就有接触,无非就是确定一个数字,然后再列出所有可能性……这个解决的办法就是穷举。题目要求我们输出所有的可能性,那么使用dfs算法穷举出所有的可能性,最后再输出就好了
1.2代码
class Solution {List<List<Integer>> res=new LinkedList<>();public List<List<Integer>> permute(int[] nums) {LinkedList<Integer> track=new LinkedList<>();backcheck(nums,track);return res;}void backcheck(int[] nums,LinkedList<Integer> track){if(track.size()==nums.length){res.add(new LinkedList<Integer>(track));return;}for(int i=0;i<nums.length;i++){if(track.contains(nums[i])){continue;}track.add(nums[i]);backcheck(nums,track);track.removeLast();}}}
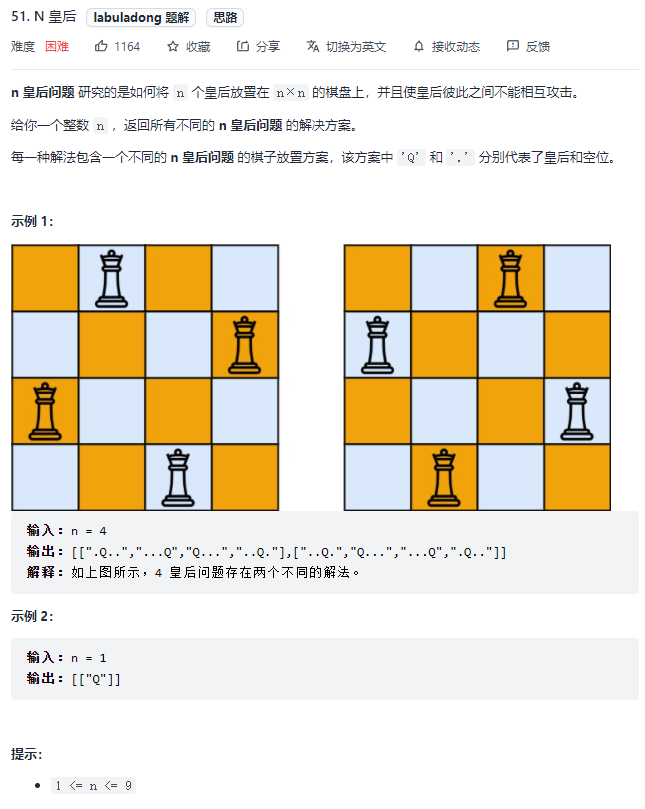
2.Leetcode51,N皇后
2.1思路分析
题目给定一个N×N的棋盘,我们就定义一个二维数组表示棋盘,要确定刚开始皇后摆放的位置,我们首先得思考:第一个棋的入口要在开头、结尾还是中间,很明显,dfs要求的递归树是一个逐级加深的树,因此我们的递归入口不应该在棋盘的中间,而应该在棋盘的第一行或者最后一行。
这个题目,我们选择递归入口为第一行。用for循环遍历,我们第一个皇后可以放在第一行的任意一个位置。放置了旗子后(做出选择),我们开始递归,此时给我们的选择有第二行的四个位置(选择列表),递归之后我们回溯,因此要撤销之前做出选择的操作。
注意:在摆放了第一个旗子之后的每一次递归,我们都要判断下一个棋子的正上方、左上方和右上方是否有棋子,如果有棋子,则违反了题目的规定(皇后能相互攻击),只有这三个方位没有皇后,我们才能做出选择。当递归到最后一层的时候,我们把整个棋盘放入结果中然后输出。
2.2代码
class Solution {List<List<String>> res=new LinkedList<>();public List<List<String>> solveNQueens(int n) {char[][] board = new char[n][n];for (int i = 0; i < n; i++) {Arrays.fill(board[i], '.');}backTrack(board, 0);return res;}public void backTrack(char[][] board, int row) {List<String> list=new LinkedList<>();int col = board[0].length;if (row == board.length) {for (int i = 0; i < row; i++) {list.add(new String(board[i]));//System.out.println(res);}res.add(new LinkedList(list));return;}for (int i = 0; i < col; i++) {if (!isValid(board, row, i)) {continue;}board[row][i] = 'Q';backTrack(board, row + 1);board[row][i] = '.';}}public boolean isValid(char[][] board,int row,int col){//检测上方for(int i=0;i<row;i++){if(board[i][col]=='Q')return false;}//检测左上for(int i=row-1,j=col-1;i>=0 && j>=0;i--,j--){if(board[i][j]=='Q')return false;}//检测右上for(int i=row-1,j=col+1;i>=0 && j<board[0].length;i--,j++){if(board[i][j]=='Q')return false;}return true;}}
3.Leetcode698.划分为k个相等的子集
通过上面两个题目的练习,我们对于回溯算法有了一个了解,接下来这个题目也没有什么不同,只不过我们可以从两个方面来给出回溯的方案。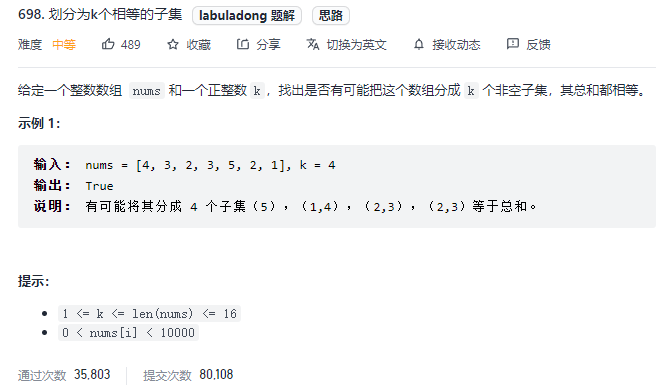
题目的意思简单来说就是给出k个桶,把数字装进桶中保证每个桶的数字之和相同
3.1代码实现
以数字的角度:遍历数组中的每一个数字,将每个数字放入k个桶中的一个
class Solution{public boolean canPartitionKSubsets(int[] nums, int k) {Arrays.sort(nums);for(int i=0,j=nums.length-1;i<j;i++,j--){int temp=nums[i];nums[i]=nums[j];nums[j]=temp;}if(k>nums.length)return false;int sum=0;int[] bucket=new int[k];for(int i=0;i<nums.length;i++){sum+=nums[i];}int target=0;if(sum%k!=0)return false;target=sum/k;return backTrack(nums,bucket,0,target);}public boolean backTrack(int[] nums,int[] bucket,int start,int target){if(start==nums.length){for(int i=0;i<bucket.length;i++){if(bucket[i]!=target){return false;}return true;}}for(int i=0;i<bucket.length;i++){if(bucket[i]+nums[start]>target){continue;}bucket[i]+=nums[start];if(backTrack(nums,bucket,start+1,target)){return true;}bucket[i]-=nums[start];}return false;}}
以桶的角度,每次选定一个桶,确定以后遍历整个数组装进桶中,装满就递归下一个桶(过程中要判断选择的数字是否已经被装入桶中)
class Solution {public boolean canPartitionKSubsets(int[] nums, int k){Arrays.sort(nums);for(int i=0,j=nums.length-1;i<j;i++,j--){int temp=nums[i];nums[i]=nums[j];nums[j]=temp;}if(k>nums.length)return false;int sum=0;for(int i=0;i<nums.length;i++){sum+=nums[i];}if(sum%k!=0){return false;}int target=sum/k;boolean[] used=new boolean[nums.length];return backTrack(nums,0,k,used,target);}public boolean backTrack(int[] nums,int bucket,int k,boolean[] used,int target){if(k==0)return true;if(bucket==target)return backTrack(nums,0,k-1,used,target);for(int i=0;i<nums.length;i++){if(used[i])continue;if(bucket+nums[i]>target)break;used[i]=true;bucket+=nums[i];if(backTrack(nums,bucket,k,used,target))return true;used[i]=false;bucket-=nums[i];}return false;}}
4.Leetcode78.子集
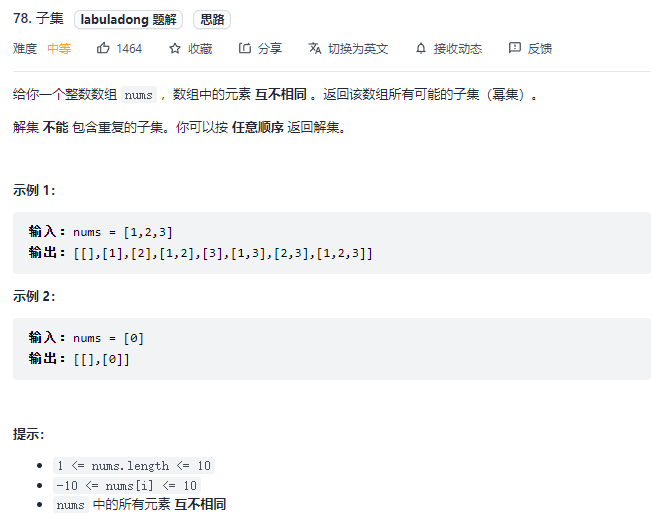
class Solution { List<List<Integer>> res=new ArrayList<>(); List<Integer> track=new ArrayList<>(); public List<List<Integer>> subsets(int[] nums) { backTrace(nums,0); return res; } public void backTrace(int[] nums,int start){ res.add(new ArrayList(track)); for(int i=start;i<nums.length;i++){ track.add(nums[i]); backTrace(nums,i+1); track.remove(track.size()-1); } } }5.排列和组合区别
6.岛屿问题
Leetcode.1020飞地的数量

很典型的岛屿问题,此类问题我们通常通过dfs实现的淹没思想——已经计算过的岛屿就把他淹没成海,从而可以继续去搜索其他的岛屿。对于这题而言:矩阵的边上的不算岛屿,所以我们把在边上的岛屿先全部淹没了,然后再用dfs重新搜索就好。
class Solution {
public int numEnclaves(int[][] grid) {
int m=grid.length;
int n=grid[0].length;
int res=0;
for(int i=0;i<m;i++){
dfs(grid,i,0);
dfs(grid,i,n-1);
}
for(int j=0;j<n;j++){
dfs(grid,0,j);
dfs(grid,m-1,j);
}
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]==1){
res++;
//dfs(grid,i,j);
}
}
}
return res;
}
public void dfs(int[][] grid,int i,int j){ //淹没
int m=grid.length;
int n=grid[0].length;
if(i<0 || j<0 || i>=m || j>=n || grid[i][j]==0){
return;
}
grid[i][j]=0;
dfs(grid,i-1,j);
dfs(grid,i+1,j);
dfs(grid,i,j+1);
dfs(grid,i,j-1);
}
}
蓝桥杯2017省赛——全球变暖
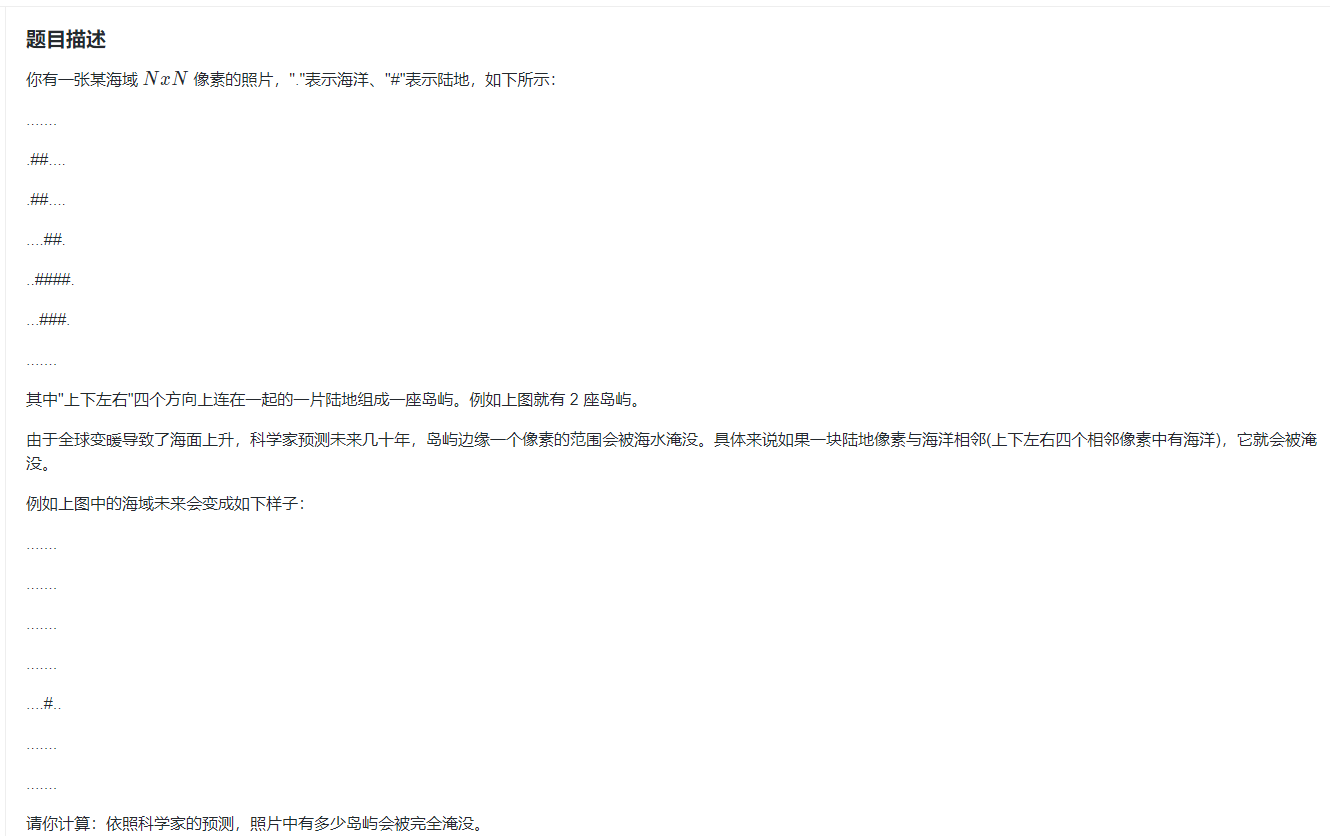
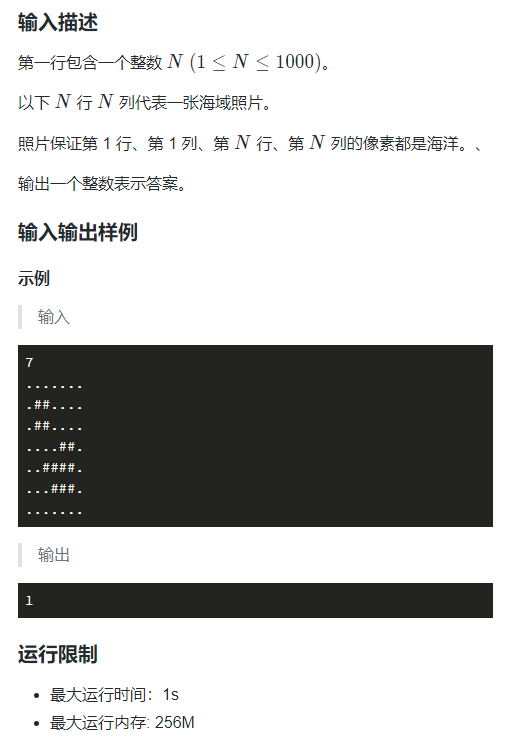
思路:对于每一个连通块,都要判断和海水相邻的陆地元素数和这个连通块总共的陆地元素数是否相等,如果想等的话,这个岛屿就会消失,否则就不会消失。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxx=1e3+100;
int d[][2]={{1,0},{0,1},{-1,0},{0,-1}};
char s[maxx][maxx];
int vis[maxx][maxx];
int n;
inline void dfs(int x,int y,int &num,int &cnt)
{
vis[x][y]=1;
num++;
if(x-1>=0&&s[x-1][y]=='.') cnt++;
else if(x+1<n&&s[x+1][y]=='.') cnt++;
else if(y-1>=0&&s[x][y-1]=='.') cnt++;
else if(y+1<n&&s[x][y+1]=='.') cnt++;
for(int i=0;i<4;i++)
{
int tx=x+d[i][0];
int ty=y+d[i][1];
if(tx<0||tx>=n||ty<0||ty>=n||vis[tx][ty]||s[tx][ty]=='.') continue;
dfs(tx,ty,num,cnt);
}
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%s",s[i]);
memset(vis,0,sizeof(vis));
int ans=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(s[i][j]=='#'&&vis[i][j]==0)
{
int num=0,cnt=0;
dfs(i,j,num,cnt);
if(num==cnt) ans++;
}
}
}
printf("%d\n",ans);
return 0;
}
————————————————
版权声明:本文为CSDN博主「starlet_kiss」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/starlet_kiss/article/details/105284665
思路:
从数组mp开始遍历,每遍历到一个未被访问过的‘#’,就开始dfs找相连的连通块,并将连通块都设为访问过的状态(使用数组vis[]标记)。
并在边搜索时,判断是否存在位置相邻的四个方向皆为‘#’,若存在则ans[]++,若一个都不存在则ans[]等于0。
最后输出ans[]值为0的个数,即为淹没岛屿的个数。
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
static int len=0;
static int[] count=new int[100004];
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
//在此输入您的代码...
int N=scan.nextInt();
scan.nextLine();
char[][] matrix=new char[N][N];
int[][] visited=new int[N][N];
int k=0;
while(k<N){
String s=scan.nextLine();
for(int i =0;i<matrix.length;i++){
matrix[k][i]=s.charAt(i);
}
k++;
}
for(int i=0;i<matrix.length;i++){
for(int j=0;j<matrix[i].length;j++){
if(matrix[i][j]=='#' && visited[i][j]!=1){
dfs(matrix,visited,i,j,len);
len++;
}
}
}
int sum=0;
for(int i=0;i<len;i++){
if(count[i]==0){
sum++;
}
}
System.out.println(sum);
scan.close();
}
public static void dfs(char[][] matrix,int[][] visited,int m,int n,int len){
if(m<0 || n<0 ||m>=matrix.length || n>=matrix[0].length)return;
if(matrix[m][n]=='.')return;
if(visited[m][n]==1)return;
visited[m][n]=1;
if(matrix[m+1][n]=='#'&& matrix[m-1][n]=='#'&&matrix[m][n-1]=='#'&&matrix[m][n+1]=='#'){
count[len]++;
}
dfs(matrix,visited,m-1,n,len);
dfs(matrix,visited,m+1,n,len);
dfs(matrix,visited,m,n-1,len);
dfs(matrix,visited,m,n+1,len);
}
}
7.NOIP2000提高组 单词接龙

输入:
5 at touch cheat choose tact a
输出:
23
- 说明/提示
样例解释:连成的龙为:atoucheatactactouchoose
1.思路分析
首先要理解题目隐含的含义:
- 首尾进行拼接的两个单词可以有多个字符的重复
- 首尾进行拼接的两个单词必不可能全部重复
在脑子里面模拟一边进行单词接龙的步骤:
给定一个开头的字符,在所有选择中找到首字符与给定开头字符相等的字符,进行拼接,符合条件的可能有多个,而我们需要的是最大的长度,所以我们每个都搜索一遍就好了。因为每个字符可以出现两次,因此我们在使用的时候要标记使用次数,在每次搜索的时候都要判断该单词是否使用已经达到了两次,如果达到了,那么这个单词就不能再使用了,那么我们就继续搜索其他可行的单词。后续的拼接我们就需要开始判断前一个单词的结尾和后一个单词的开头有多少的重复字符,那么我们又需要一个函数来寻找到总共有多少个重复的字符,最后拼接的时候把
的长度相加再减去重复的字符就是拼接后的长度
2.代码
import java.util.Scanner;
public class Main {
static int len=0;
static int l=0;
private static String[] arr;
private static int[] cc;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
sc.nextLine();
arr = new String[n];
cc = new int[n];
for(int i=0;i<n;i++){
arr[i]=sc.nextLine();
}
String start=sc.nextLine();
for(int i = 0; i< arr.length; i++){
if(arr[i].charAt(0)==start.charAt(0)){
cc[i]++;
len= arr[i].length();
dfs(i,len);
cc[i]--;
len=0;
}
}
System.out.println(l);
}
private static void dfs(int index,int len) {//计算龙的长度
l=Math.max(len,l);
for(int i=0;i<arr.length;i++){
int p=find(index,i);//表示重叠了多少个字符
if(cc[i]<2&&p>0){
cc[i]++;
len=len+arr[i].length()-p;
dfs(i,len);
cc[i]--;
len=len-arr[i].length()+p;
}
}
}
private static int find(int index, int x) {
int lx=arr[index].length();
int ly=arr[x].length();
for(int i=1;i<Math.min(lx,ly);i++){//表示从哪一位开始比
boolean flag=true;
for(int j=0;j<i;j++){
if(arr[index].charAt(lx-i+j)!=arr[x].charAt(j)){
flag=false;
break;
}
}
if(flag)return i;
}
return 0;
}
}