1、基本运算

在AES中选择的不可约多项式是p(x)=x+x+x+x+1，余式的次数至多是7次，共2=256个多项式，这256个余式构成了一个有限域GF(28)。

📍字节在GF(2)上的表示

字节b用二进制表示为b=bbbbbbbb为有限域GF(2)上的域元素，若用多项式表示，b可看作是多项式的系数，b∈{0,1}，则字节b对应多项式为：bx+bx+bx+bx+bx+bx+bx+b

例如：字节‘57’（十六进制数）对应的二进制为01010111，为GF(2)上域元素，字节‘57’对应的多项式为x+x+x+x+1。
通俗一点：

二进制 0 1 0 1 0 1 1 1
多项式 x x x x x x x x(1)
遇到[1]留下 x x x x 1
结果 x+x+x+x+1

📍GF(2) 上两个域元素的和

GF(2)上两个域元素的和对应的多项式仍然是一个次数不超过7的多项式，其多项式系数等于两个元素对应多项式系数的模2加，即域元素对应二进制按位异或运算。
例如：‘57’+‘83’=‘D4’
用多项式表示为：(x+x+x+x+1)⊕(x+x+1)≡x+x+x+x( mod p(x) )
mod，是一个数学运算符号。
用二进制表示为： 01010111
⊕ 10000011
11010100
直接表示： x+ x+1
⊕ x+x+x~~+x+1 ~~
x+x+x+x(mod p(x))

由于每个元素的加法逆元等于自己，所以有限域减法和加法相同。

📍GF(2) 上两个域元素的乘

要计算GF(2)上域元素的乘法，必须先确定一个GF(2)上的8次不可约多项式；GF(2)上两个元素的乘积就是这两个多项式的模乘。
在Rijndael密码中，这个8次不可约多项式确定为：p(x)= x+x+x+x+1，十六进制表示为‘11B’
例如：‘57’·‘83’=‘C1’可表示为以下的多项式乘法：
(x+x+x+x+1) · (x+x+1) ≡ x+x+1( mod p(x) )

①分项相乘，做⊕： (x+x+x+x+1)x———————— x+x+x+x+x~~ (x+x+x+x+1)x ———————— ~~ x~~ +x +x+x~~+x x+x+x+x+1 ———————— ⊕ x +x +x~~+x+1 x+x+x+x+x+x+x+x +1 ②、与p(x)= x+x+x+x+1做⊕，消除到低于x： ~~x+x+x+x+x+x+x+x+1 x(x+x+x+x+1)———— ⊕ x+x+x+x+x x +x+x+1 x(x+x+x+x+1)———— ⊕ ~~ x11~~ +x7+x6 +x4+x3 x7+x6+1 所以11000001，转化为十六进制也就是C1

📍x乘法

GF(2)上还定义了一个运算，称之为x乘法，其定义为：
x·b(x)≡bx+bx+bx+bx+bx+bx+bx+bx( mod p(x) )
如果b=0，求模结果不变，否则为乘积结果减去p(x)，即求乘积结果与p(x)的异或。
由此得出x（十六进制数‘02’）乘b(x)可以先对b(x)在字节内左移一位（最后一位补0）。
若b=1，则再与‘1B’（其二进制为00011011）做逐比特异或来实现，而任意常数乘法可以通过对中间结果相加实现。

已知：b(x)≡bx+bx+bx+bx+bx+bx+bx+b( mod p(x) ) 所以：x·b(x)≡bx+bx+bx+bx+bx+bx+bx+bx( mod p(x) ) 当b=0时： x·b(x)≡bx+bx+bx+bx+bx+bx+bx+0( mod p(x) ) 相比b(x)，每一位都往前一步，转换为二进制的话，确实后面加0即可 当b=1时： x·b(x)≡x+bx+bx+bx+bx+bx+bx+bx+0( mod p(x) ) 其实用到 p(x)= x+x+x+x+1 也就是‘11B’，因为b是1，所以p(x)中x8是0，所以是‘1B’，实则是与p(x)做消项操作。

📍GF(2)上域元素的乘法逆元

在有限域GF(2)中，域元素的乘法满足交换律，且有单位元，并且每个域元素都有乘法逆元。在GF(2)中求乘法逆元可利用多项式的扩展的欧几里得算法计算出来。
求次数小于8的非零多项式b(x)的乘法逆元，首先利用多项式的扩展欧几里得算法得出两个多项式a(x)和c(x)，使得满足b(x)a(x)+p(x)c(x)=1， 即满足a(x)·b(x) ≡1 mod p(x)，因此a(x)是b(x)的乘法逆元。

2、AES密码概述

  • DES算法，密钥长度短，存在弱密码和半弱密码，经不住穷举分析
  • 1994年，美国颁布新密码标准EES，但在1995年5月，被贝尔实验室的博士生成功破解，7月美国政府放弃EES算法。
  • 1997年，美国公开征集AES算法
  • 2000年10月，美国政府正式宣布选中比利时密码学Joan Daemen和Vincent
  • Rijmen提出的RIJNDAEL算法作为AES，2001年11月，正式颁布AES作为美国国家
  • 标准。
  • AES 算法的设计策略是针对差分分析和线性分析提出来的，是一个分组迭代密码，采用128数据分组长度，具有可变的密钥长度128、192、256位。
  • AES算法属于分组密码，不是Feistel结构，而是SP结构。
  • AES算法不是对合运算：加密与解密使用不同的算法。

  • AES算法综合运用了置换、代替、代数等多种密码技术

    3、AES的加密过程

    📍整体结构

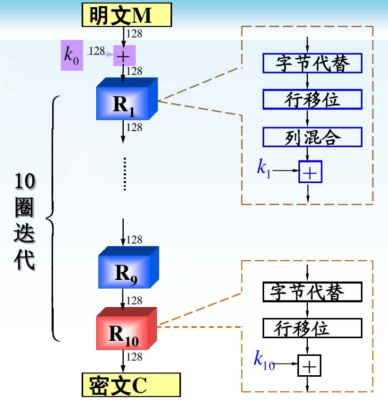
    image.png
    基本轮函数加迭代，圈数可变，圈数>=10：

    • 一般轮数：
      • S盒变换ByteSub
      • 行移位变换ShiftRow
      • 列混合变换MixColumn
      • 轮密钥加变换AddRoundKey
    • 最后一轮：
      • S盒变换ByteSub
      • 行移位变换ShiftRow
      • 轮密钥加变换AddRoundKey

        📍AES的数据处理方式

        📌AES的数据处理方式

  • 字节、字

  • 状态

    📌状态

  • 加解密过程中的中间数据

  • 以字节为元素的4行Nb列的矩阵，或者二维数组

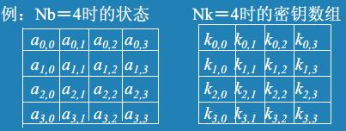
image.png

  • 符号：
    • Nb —明文数据长度
      • 数据块长度除以32，如128/32=4、192/32=6、256/32=8
    • Nk —密钥数据长度，同Nb
    • Nr —迭代圈数
  • Nb、Nk、Nr之间的关系： | Nr | Nb=4 | Nb=6 | Nb=8 | | —- | —- | —- | —- | | Nk=4 | 10 | 12 | 14 | | Nk=6 | 12 | 12 | 14 | | Nk=8 | 14 | 14 | 14 |

📍AES初始状态

AES算法的分组长度固定为128比特，以字节为基本单位转换为状态字节，依顺序a, a, a, a, a, … a, a，前4个字节组成第1列，后四个字节组成第2列，依次类推，AES算法明文分组可以构成一个4×4的字节矩阵，加密结束时，输出也是从状态字节中按相同的顺序提取。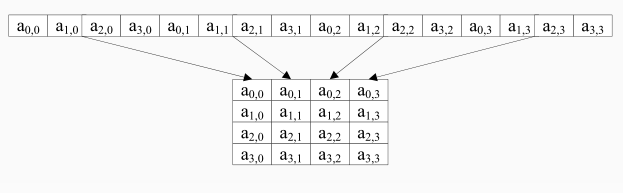
image.png

📌AES初始状态举例

下面我们以一个128位块为例，开始分别介绍AES加密算法基本变换的具体过程。
为了表达简洁，下面的中间结果都用16进制来表示。则128比特二进制示例块用16进制表示则对应为0x 80 5E 6A 36 53 25 3A 66 63 35 69 03 20 6C 28 06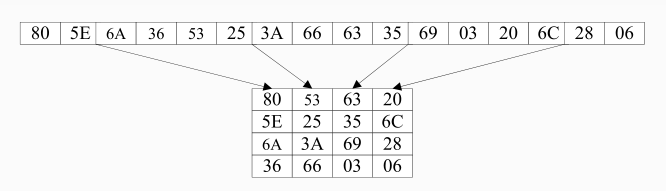
image.png

📍AES的加密过程—S盒变换ByteSub(State)

📌概念

  • S盒变换是AES的唯一的非线性变换，是AES安全的关键。
  • AES使用16个相同的S盒; DES使用8个不相同的S盒。
  • AES的的S盒8位输入8位输出;DES的S盒有6位输入4位输出。

image.png

📌映射方法

把输入字节的高4位作为S盒的行值，低4位作为列值，然后取出S盒中对应行和列的元素作为输出。
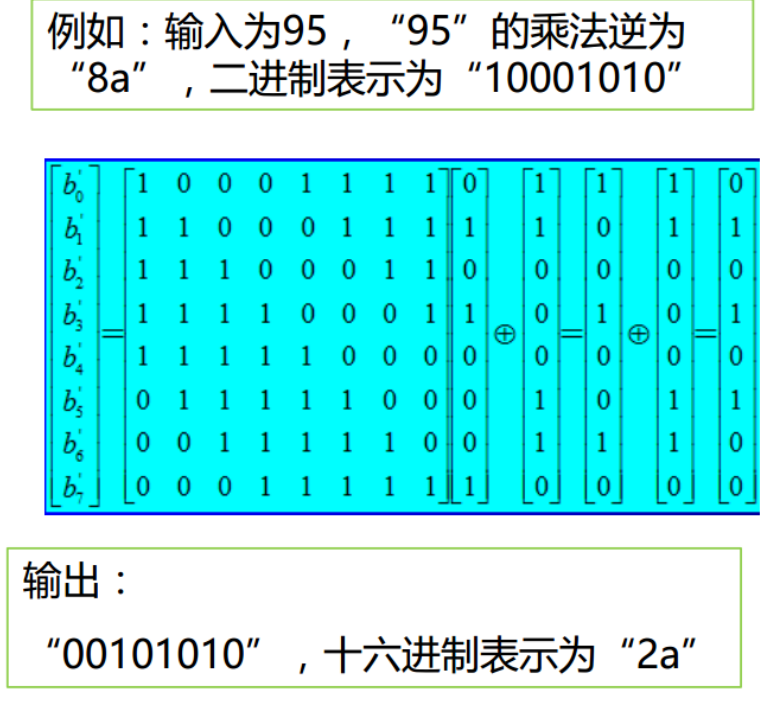
例如：输入95，通过S盒变换，输出为2aimage.png

9为行，5为列，相交得出2a

📌S盒变换的两个步骤

  1. 将输入字节用其GF(2)上的乘法逆元来代替
  2. 对1.的结果作如下的仿射变换**__37课的时候再说

image.pngimage.png

📍AES的加密过程—行移位变换ShiftRow

📌概念

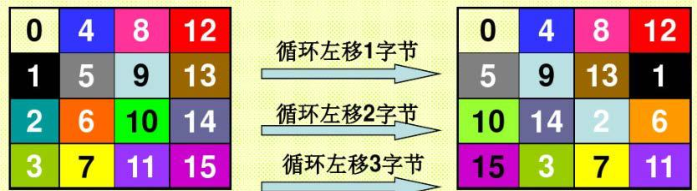
  • 行移位变换对状态的行进行循环左移。
  • 第0行不移位；第1行移C字节，第2行移C字节；
  • 第3行移C3字节。
  • C、C、C按表取值

AES的Nb固定为4，下面两行针对Rijndael算法

Nb（列数） C0（第1行） C1（第2行） C2（第3行） C4（第4行）
4 0 1 2 3
6 0 1 2 3
8 0 1 2 3

📌AES加密过程—行移位

image.png

📍AES加密过程—列混合变换MixColumn(State)

📌概念

  • 列混合变换把状态的列视为GF(28)上的多项上的多项式a(x)，乘以一个固定搞的多项式c(x)，并 mod x+1：b(x)=a(x)c(x) mod x+1，其中c(x)=03x+01x+01x+02

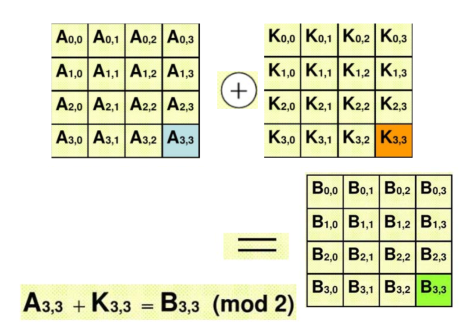
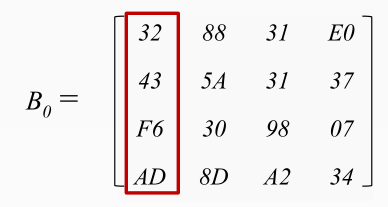
image.png
image.pngimage.png

  • 列混合变换属于代替变换

    📍AES加密过程—轮密钥加变换AddRoundKey(State)

    📌概念

  • 把圈密钥与状态进行模2加

1.png

  • 圈密钥根据密钥产生算法

  • 圈密钥长度=数据块长度

    📌轮密钥产生

  • 轮密钥根据密钥产生算法，通过用户密钥K0得到轮密钥。

  • 密钥产生分两步进行：
    • 密钥扩展和：将用户密钥扩展为一个扩展密钥
    • 轮密钥选择：从扩展密钥中选出轮密钥

      🚩密钥扩展

      ①密钥扩展产生扩展
      ②用一个字元素的一维数组W[Nb*(Nr+1)] 表示扩展密钥
      ③用户密钥放在数组最开始的Nk个字中
      ④其它的字由它前面的字经过处理后得到
      ⑤有Nk≤6和 Nk>6 两种密钥扩展算法

      🚩密钥选择

      轮密钥选择根据分组的大小，依次从扩展密钥中取出轮密钥。

      4、AES加密实例

      采用AES加密：
      密钥为 2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C
      明文为 32 43 F6 AD 88 5A 30 8D 31 31 98 A2 E0 37 07 34

① 写出最初的State的值

求明文State，做矩阵 image.png

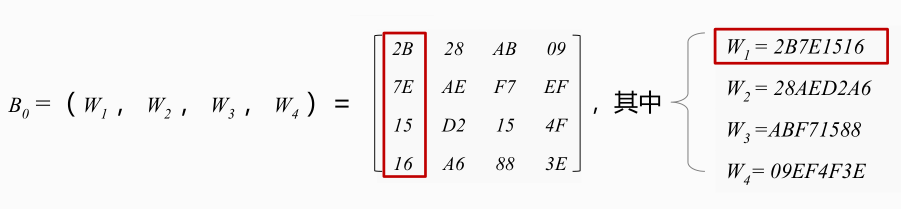
② 写出密钥扩展数组中的前8个字节

求密钥的矩阵，字节就是元素，前8个字节组成一个字，所以写出第一个字，就可以得出 微信截图_20190920144523.png

密钥扩展数组中前8个字节为W ，W ，即2b 7e 15 16 28 ae d2 a6

③ 写出初始轮密钥加后State的值
④ 写出字节代换后State的值
⑤ 写出行移位后的State的值
⑥ 写出列混淆后State的值

5、AES安全性

  • 第一步到最后一步都用了轮密钥加，因为任何没有密钥参与的变换都是容易被攻破
    • DES的IP和IP都没有密钥参与
  • 可抗击穷举密钥的攻击
    • 可抵抗穷举搜索攻击：因为AES的密钥长度可变，针对128/192/256bit的密钥，足以抵抗琼剧院搜索攻击
    • 可抗击线性攻击：经过4轮变换后，线性分析无效
    • 可抗击差分攻击：经过8轮变换后，差分攻击无效
  • 不存在弱密钥
    • 该算法对密钥的选择没有任何限制，还没有发现弱密钥

太难了···