📍密码学基础概念

📌密码学

密码编制学：研究密码编制
密码分析学：研究密码破译

📌密码学发展的三个阶段

• 古代加密方法（手工阶段）
• 古典密码（机械阶段）：如置换密码
• 近代密码（计算机阶段）

  📌近代密码学的标志

  1949年，香农发表《保密系统的通信理论》，标志：密码学形成一门学科
  1976年，W.Diffie和M.Hellman，发表《New Directions in Cryptography》
  1977年，美国颁布数据加密标准DES

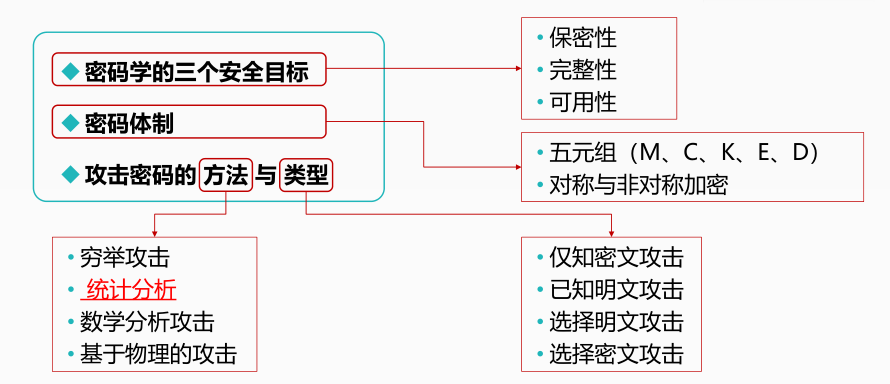
📍信息安全的基本安全目标

📌保密性

定义

确保信息仅被合法用户使用

常用的保密技术

• 防侦收
• 防辐射
• 数据加密

• 物理保密：如隔离

  📌完整性

  定义

  确保信息未经授权不能进行改变的特性

  影响完整性的因素

• 设备孤战

• 误码
• 人为攻击

• 病毒

  📌可用性

  定义

  信息可被授权实体访问并按需求使用的特性

  度量

  正常使用时间/应该工作时间

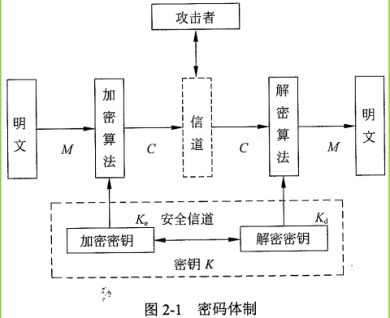
  📍密码体制

  📌密码体制的五元组(M,C,K,E,D)

• 明文空间M：全体明文的集合

• 密文空间C：全体密文的集合
• 密钥空间K：全体密钥的集合，=
• 加密算法E：一族由M到C的加密变换

• 解密算法D：一族由C到M的解密变换

  📌对称与非对称密码体制

  对称密码体制

  Kd=Ke，或容易推到出对方，又称单密钥密码体制或传统密码体制

  非对称密码体制

  Kd!=Ke，或由Ke不能推出Kd，又称为公开密钥密码体制
  

  📍攻击密码的方法与类型

  📌攻击密码的三种方法

• 穷举攻击：增大密钥空间

• 统计分析：分析密文和明文的统计规律进行破译

• 数据分析攻击：选用具有坚实数学基础和足够复杂的加密算法

  📌基于物理的攻击（侧击）

• 主要集中在功耗攻击、电磁场攻击、时间攻击。

• 功耗攻击是最强有力的手段之一，与传统密码分析学相比，这些攻击手段攻击效果显著。

  📍密码系统的分类

  📌按明文交换到密文的操作类型

• 置换密码

• 代替密码

  📌按密钥使用的数量

• 单密钥密码：对称

DES、3DES、AES、SM4、IDEA、RC5

• 双密钥密码：非对称

RSA、Elgamal、ECC、SM2

📌按密钥的使用方法

• 分组密码

DES、AES、SM4、IDEA

• 序列密码

RC4

📌不可逆

• Hash函数

MD5、SHA、SM3

📍密码算法的分类

📌按保密内容分类

• 受限制的（restricted）算法：算法的保密性基于保持算法的秘密。

• 基于密钥（key-based）的算法：算法的保密性基于对密钥的保密。

  📌按照密钥的特点分类

• 对称密码算法（symmetric cipher)：又称传统密码算法（conventional cipher)，就是加密密钥和解密密钥相同，或实质上等同，即从一个易于推出另一个。又称秘密密钥算法或单密钥算法。

• 非对称密钥算法（asymmetric cipher）:加密密钥和解密密钥不相同，从一个很难推出另一个。又称公开密钥算法（public-key cipher）。

  公开密钥算法用一个密钥进行加密, 而用另一个进行解密.其中的加密密钥可以公开，又称公开密钥（public key)，简称公钥。解密密钥必须保密，又称私人密钥（private key），简称私钥。

📌按照明文的处理方法

• 分组密码（block cipher）:将明文分成固定长度的组，用同一密钥和算法对每一块加密，输出也是固定长度的密文。
• 流密码（stream cipher）:又称序列密码。序列密码每次加密一位或一字节的明文，也可以称为流密码。

（序列密码是手工和机械密码时代的主流）

📌对称密钥密码又可分

• 分组密码

每次对一块数据加密
多数网络加密应用
DES、IDEA、RC6、Rijndael

• 流密码

每次对一位或一字节加密
手机
One-time padding、Vigenére、Vernam

📌公开密钥密码

• 大部分是分组密码，只有概率密码体制属于流密码
• 每次对一块数据加密
• 数字签名,身份鉴别
• RSA、ECC、ElGamal

• 加密解密速度慢

  📍Kerckhoff原则（柯克霍夫）

• 1883年Kerchoffs第一次明确提出了编码的原则：加密算法应建立在算法的公开不影响明文和密钥的安全的基础上。

• 这一原则已得到普遍承认，成为判定密码强度的衡量标准，实际上也成为古典密码和现代密码的分界线。

  📍对密钥系统的攻击类型

• 仅知密文攻击（Ciphertext-only attack）

加密算法
截获的部分密文

• 已知明文攻击（Know-plaintext attack）

加密算法
截获的部分密文
一个或多个明密文对

• 选择明文攻击Chosen-plaintext-attack）

加密算法
截获的部分密文
自己选择的明文消息，及由密钥产生的相应密文

• 选择密文攻击（Chosen-ciphertext attack）

加密算法
截获的部分密文
自己选择的密文消息，及相应的被解密的明文
仅知密文攻击是最困难的；上述攻击的强度是递增的；
一个密码体制是安全的，通常是指在前三种攻击下的安全性。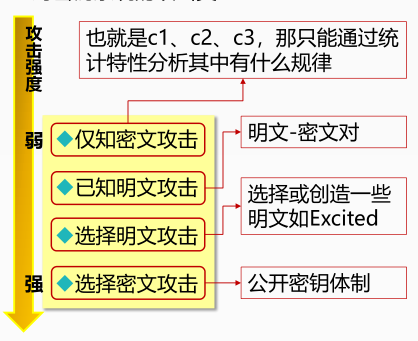

📍古典密码

📌置换密码

• 把明文中的字母重新排列，字母本身不变，但其位置改变了。

• 经不起已知明文攻击。

  📌代替密码

• 使用密文字母表中的字母或字母组代替明文字母或字母组，各字母或字母组的相对位置不变，但本身发生了变化。

  常见代替密码

• 加法密码

• 乘法密码

• 仿射密码

  加法密码

  设计思想

• f(a)=b=a

• j=(i+k) mod n

• 其中：a ∈A，k是满足0

  举例

  凯撒密码Caesar ：是经典的加法密码，即k=3的加密方法。
  
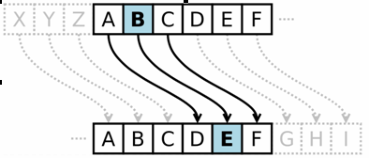
  明文 sce， 其中26个字母与整数0-25一一对应， 经凯撒密码加密后，密文是什么？vfh

  乘法密码

  设计思想

• f(a)=b=a

• j=ik mod n
• k与n互素，即（k，n）=1

• 预先知道消息元素的个数n

  举例

  若明文A={A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} 取k=5，则（5，26）= 1
  

  仿射密码

  设计思想

• f(a)=b=a

• j=(ik +k) mod n
• (k，n)=1，0 ≦ k ≦ n，且不允许同时有k=1 ，k=0
• 结合了乘法密码和加法密码

• 密钥空间：12*26-1=312-1=311

  举例

  设密钥k=（5，3），利用仿射密码加密明文dog
  3个字母对应的数值是：3、14和6，分别加密如下：
  (35+3) mod 26=18 mod 26=18, 对应字母s
  (145+3) mod 26=73 mod 26=21, 对应字母v
  (6*5+3) mod 26=33 mod 26=7, 对应字母h
  对应的密文是：svh

  📌代数密码：vernam密码（vernam）

  vernam密码（vernam）的定义与实现

• Vernam密码的明文、密钥和密文均用二元数字序列表示。

• 设明文M =（m, m ,…,m ）,密钥K =（k, k ,…,k），密文C =（c, c ,…, c）
• 其中，m 、k 、c ∈GF（2），则

c = m ⊕ k， 即模2加，也就是异或运算。也称为代数密码，也称为一次一密。

举例

明文： DATA （68、65、84、65）
二进制：1000100 ，1000001，1010100，1000001
密钥： LAMB （76、65、77、66）
二进制：1001100， 1000001，1001101， 1000010
密文：0001000， 0000000，0011001， 0000011

vernam密码（vernam）的特点与不足

特点

• 加密与解密算法相同，都是模2加运算
• 属于对合运算，因为正变换和逆变换相同，即f=f

• 实现比较方便，工作量减半

  不足

  经不起已知明文攻击，因为：k = c ⊕ m
  同一密钥重复使用或密钥本身重复，则Vernam密码将是不安全的

  一次一密的特点

• 密钥是真正的随机序列

• 密钥至少和明文一样长

• 一个密钥只能使用一次

  📍古典密码的破译

• 穷举分析

• 统计分析