主题

pytorch 学习与实践

问题描述

一个简单的回归问题，输入是 100 组数据，每组数据有 1000 个特征；输出也是 100 组数据，但只需要 10 个特征。

问题分析

根据输入特征和输出特征数量，输入层节点和输出层节点个数应该分别是 1000 和 10 个。假设只设置一个隐藏层，节点个数为 n，网络结构如下图所示：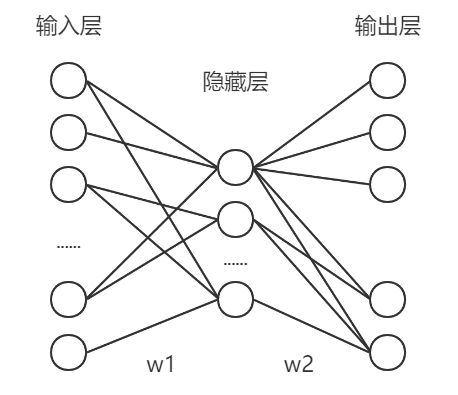
image.png
由此可知，周报四 - 图2

设置超参数：

  1. 训练次数：epochn = 10000，训练一万次。
  2. 学习效率：0.000001

损失函数的定义：
周报四 - 图3，即预测输出与样本值差值的平方。
我们的目标就是探索一个适当的 n 的值，使得损失最小。

代码如下：

  1. # a simple regression problem
  2. # x is input, including 100 datas, each data has 1000 features
  3. # y is output, including 100 datas, each data has 10 features
  4. # thus, 1000 nodes for input layer and 10 nodes for output layer
  5. # presume only 1 hidden layer with n nodes
  7. import torch
  9. def main():
  10.     # define input and output, no need tracing grad
  11.     x = torch.randn(100, 1000, requires_grad=False)
  12.     y = torch.randn(100, 10, requires_grad=False)
  14.     # assume n is 100
  15.     # define weight matrix, need tracing grad
  16.     w1 = torch.randn(1000, 100, requires_grad=True)
  17.     w2 = torch.randn(100, 10, requires_grad=True)
  19.     # define hyper parameters
  20.     epoch_n = 10000
  21.     learn_rate = 1e-6
  23.     # train
  24.     for epoch in range(epoch_n):
  25.         # forward
  26.         h1 = x.mm(w1).clamp(min=0)
  27.         y_pred = h1.mm(w2)
  29.         # backward
  30.         loss = (y_pred - y).pow(2).sum()
  31.         loss.backward()
  33.         # update
  34.         with torch.no_grad():
  35.             w1 -= learn_rate * w1.grad
  36.             w2 -= learn_rate * w2.grad
  37.             w1.grad.zero_()
  38.             w2.grad.zero_()
  40.         print(epoch, "-loss:", loss.item())
  43. if __name__ == '__main__':
  44.     main()

关于隐藏层节点个数的设置，没有什么科学依据，都是凭借一些经验，比如：

  1. 周报四 - 图4

    其中： 周报四 - 图5 是输入层神经元个数；
    周报四 - 图6是输出层神经元个数；
    周报四 - 图7是训练集的样本数；
    α 是可以自取的任意值变量，通常范围可取 2-10。

  2. 隐藏神经元的数量应在输入层的大小和输出层的大小之间。

  3. 隐藏神经元的数量应为输入层大小的2/3加上输出层大小的2/3。
  4. 隐藏神经元的数量应小于输入层大小的两倍。

在该问题中，经过反复试验，发现 n = 80 时网络收敛得较快且损失也较小。

  1. n = 100 时，loss 为 2.86
  2. n = 80 时，loss 为 0.16

image.png