前言

总结主要对小学期所学内容进行一个汇总，主要从学习到的理论知识和实践应用两个方面进行总结。

理论知识

人工智能与机器学习

人工智能领域里，机器学习是它的一种实现方法，机器学习中有一类算法叫神经网络，三者是包含关系。
我认为，机器学习的目的是：根据输入训练学习模型，然后根据模型预测结果。
分类：

1. 监督学习：训练样本有输入，也有相应的实际值作对照。
2. 无监督学习：训练样本只有输入，没有相应的实际值作对照。

线性回归

主要总结最简单的线性网络模型。

神经网络的组成

神经网络是按照一定规则把神经元连接在一起而构成的网络，不同的神经网络有不同的连接规则。
按层次划分神经网络：最左边一层输入层 + 中间多层隐藏层 + 最右边一层输出层。
深度神经网络：隐藏层层数大于 2 层的神经网络。
全连接神经网络的连接规则如下：

1. 同一层的神经元之间没有连接。
2. 第 n 层的每个神经元和第 n-1 层的所有神经元相连（全连接的含义），第 n-1 层神经元的输出就是第 n 层神经元的输入。
3. 每个连接都有一个权值。

神经元（感知器）的组成

神经元也叫感知器。

1. 输入与权值：输入 ，权值
2. 输出：神经元的输出 ，b 为偏置值，若令 ，则可以把偏置值视为输入永远为 1 的权值。
3. 激活函数：可以说是激活函数决定了神经元的作用，根据上述输出的计算公式，可以计算出自变量的值，因变量 y 到底是多少还不知道，这时候就要选择一个函数来把自变量和因变量映射起来了，这个函数的选取可能涉及许多学科的知识，以下是把一个阶跃函数作为激活函数的例子：

感知器的训练规则：
由神经元的组成的可知，若想根据输入预测输出，需要确定两样东西：权值和激活函数。
激活函数的确定过于深奥，这里就直接用给出的阶跃函数；感知器的迭代规则如下：

初始 w 和 b 置 0
：称为学习效率的常数，作用是控制每一步调整权的幅度。
：训练样本中输入对应的实际输出值。
：感知器的输出值。

线性单元

激活函数为可导线性函数的神经元。
线性单元用来解决回归问题。

线性模型

模型的目的就是根据输入预测输出。
输入 称为输入特征
输出 称为假设，其中

目标函数

线性单元的目标函数的作用是：确定合适的，以提高模型的准确度（即使得模型输出 y’ 与实际值 y，也称 label 的尽可能接近），有关概念如下：
单个样本误差：
模型误差：就是所有样本误差之和
输出 y’ 的计算公式 与 有关，当输入 确定时，E 是 w 的函数，即

现在的目标就是求取合适的 w 使得 E 最小，数学上称为优化问题，E 称为目标函数。

优化算法

优化算法就是用来解决优化问题的，即求取合适的 w 使得 E 最小。
梯度下降优化算法和随机梯度下降算法，前者需要遍历所有样本，而后者只计算一个样本。
数学知识过于硬核，就不抄教程了。

运行实例

运行与运算感知器的例子，使用插桩法打印输出观察权值变化。



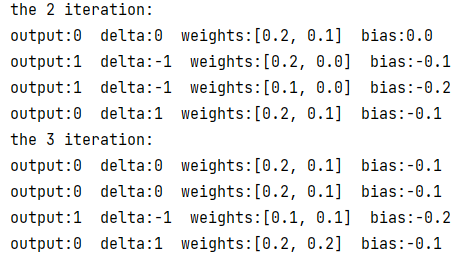
可以看到，从第 4 轮迭代的第 3 次训练开始，感知器的权值和偏置值已经稳定，结果和测试如下：

线性单元

这里仅展示了部分迭代结果，由此可知 10 次迭代内 w 和 b 没有稳定下来。
拟合结果如下：

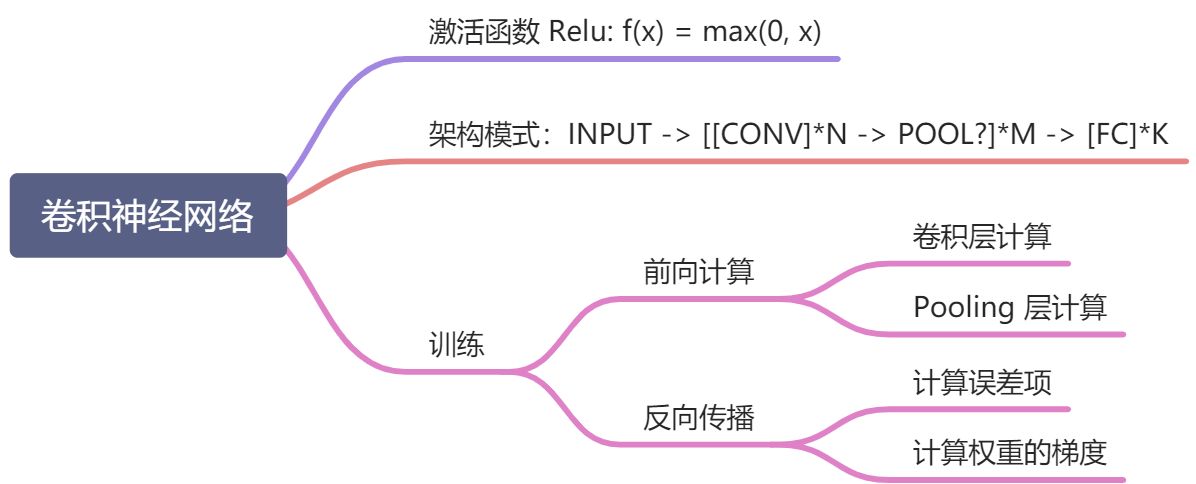
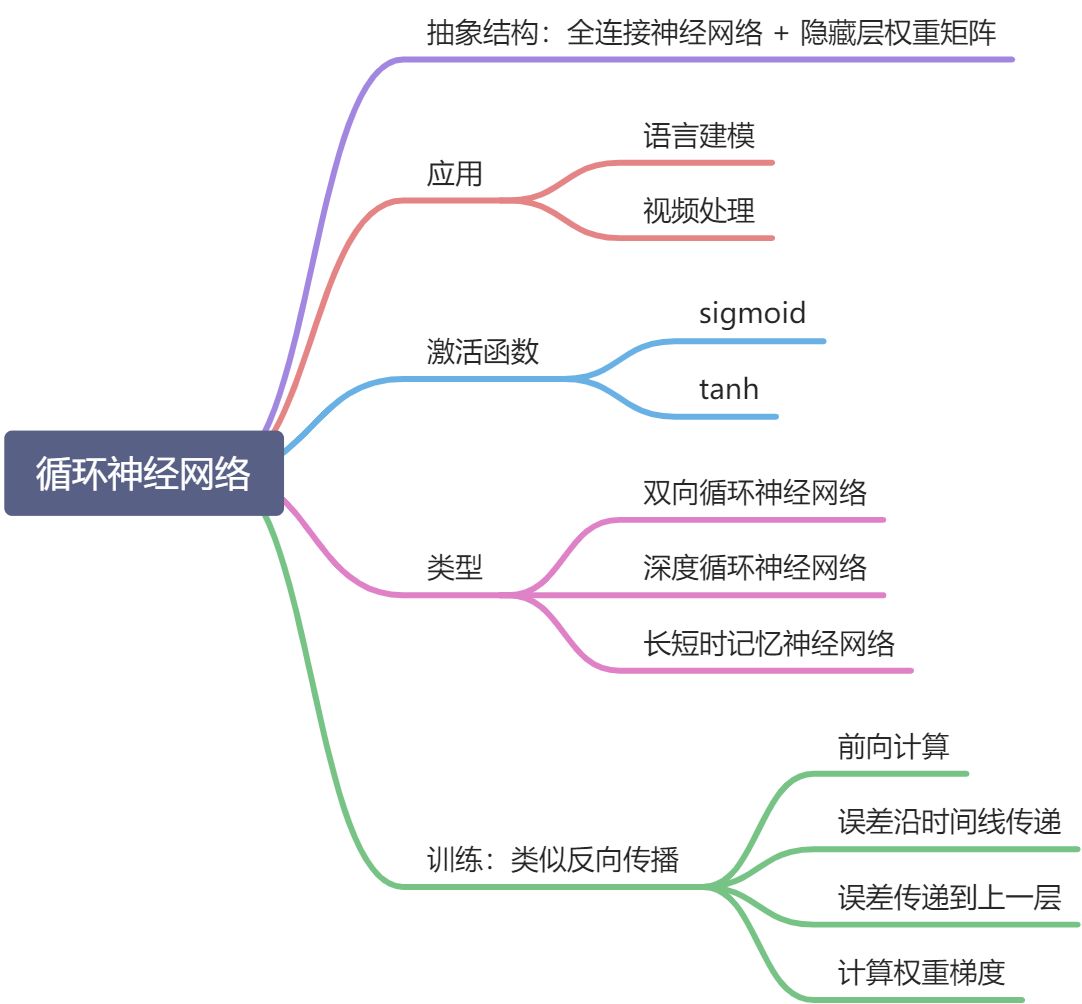
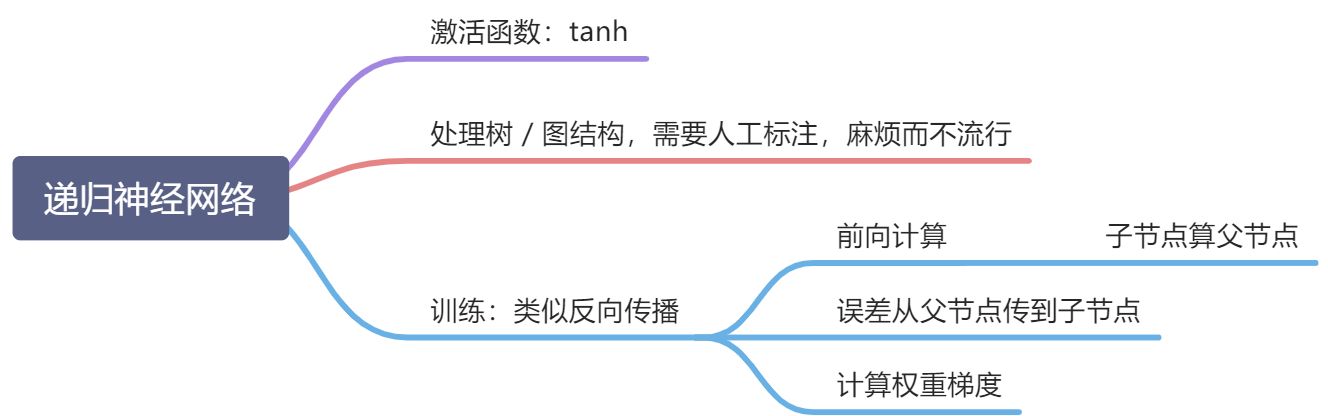
经典神经网络知识图谱

实践

问题描述

一个简单的回归问题，输入是 100 组数据，每组数据有 1000 个特征；输出也是 100 组数据，但只需要 10 个特征。

问题分析

根据输入特征和输出特征数量，输入层节点和输出层节点个数应该分别是 1000 和 10 个。假设只设置一个隐藏层，节点个数为 n，网络结构如下图所示：

由此可知，

设置超参数：

1. 训练次数：epochn = 10000，训练一万次。
2. 学习效率：0.000001

损失函数的定义：
，即预测输出与样本值差值的平方。
我们的目标就是探索一个适当的 n 的值，使得损失最小。

代码如下：

# a simple regression problem
# x is input, including 100 datas, each data has 1000 features
# y is output, including 100 datas, each data has 10 features
# thus, 1000 nodes for input layer and 10 nodes for output layer
# presume only 1 hidden layer with n nodes
import torch
def main():
    # define input and output, no need tracing grad
    x = torch.randn(100, 1000, requires_grad=False)
    y = torch.randn(100, 10, requires_grad=False)
    # assume n is 100
    # define weight matrix, need tracing grad
    w1 = torch.randn(1000, 100, requires_grad=True)
    w2 = torch.randn(100, 10, requires_grad=True)
    # define hyper parameters
    epoch_n = 10000
    learn_rate = 1e-6
    # train
    for epoch in range(epoch_n):
        # forward
        h1 = x.mm(w1).clamp(min=0)
        y_pred = h1.mm(w2)
        # backward
        loss = (y_pred - y).pow(2).sum()
        loss.backward()
        # update
        with torch.no_grad():
            w1 -= learn_rate * w1.grad
            w2 -= learn_rate * w2.grad
            w1.grad.zero_()
            w2.grad.zero_()
        print(epoch, "-loss:", loss.item())
if __name__ == '__main__':
    main()

关于隐藏层节点个数的设置，没有什么科学依据，都是凭借一些经验，比如：

1. 

   其中： 是输入层神经元个数；
   是输出层神经元个数；
   是训练集的样本数；
   α 是可以自取的任意值变量，通常范围可取 2-10。

2. 隐藏神经元的数量应在输入层的大小和输出层的大小之间。

3. 隐藏神经元的数量应为输入层大小的2/3加上输出层大小的2/3。
4. 隐藏神经元的数量应小于输入层大小的两倍。

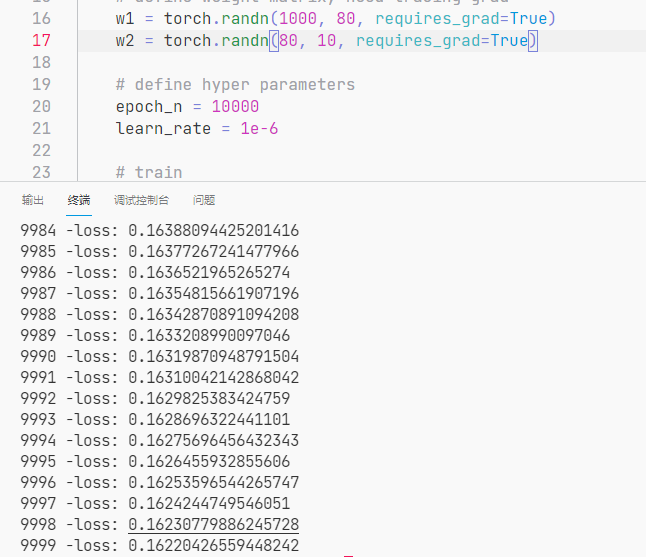
在该问题中，经过反复试验，发现 n = 80 时网络收敛得较快且损失也较小。

1. n = 100 时，loss 为 2.86
2. n = 80 时，loss 为 0.16

收获与体会

通过小学期的学习，我初步入门了机器学习领域，熟悉了经典的神经网络模型包括卷积神经网络、循环神经网络以及递归神经网络等，并且对它们的特点和应用场景有一定的理解。除此之外，我还学会了通过pytorch搭建一个最简单的网络模型并且训练它，最终获得理想的预测效果。