菲波那切数列的顺序是 0,1,1,2,3,5,8,13,21,….。

递归形式

按照我们以前的思路，很容易就想到递归来做。这里以 fib(6) 来展开得到的结果如下，它的一个时间复杂度是 O(2n)。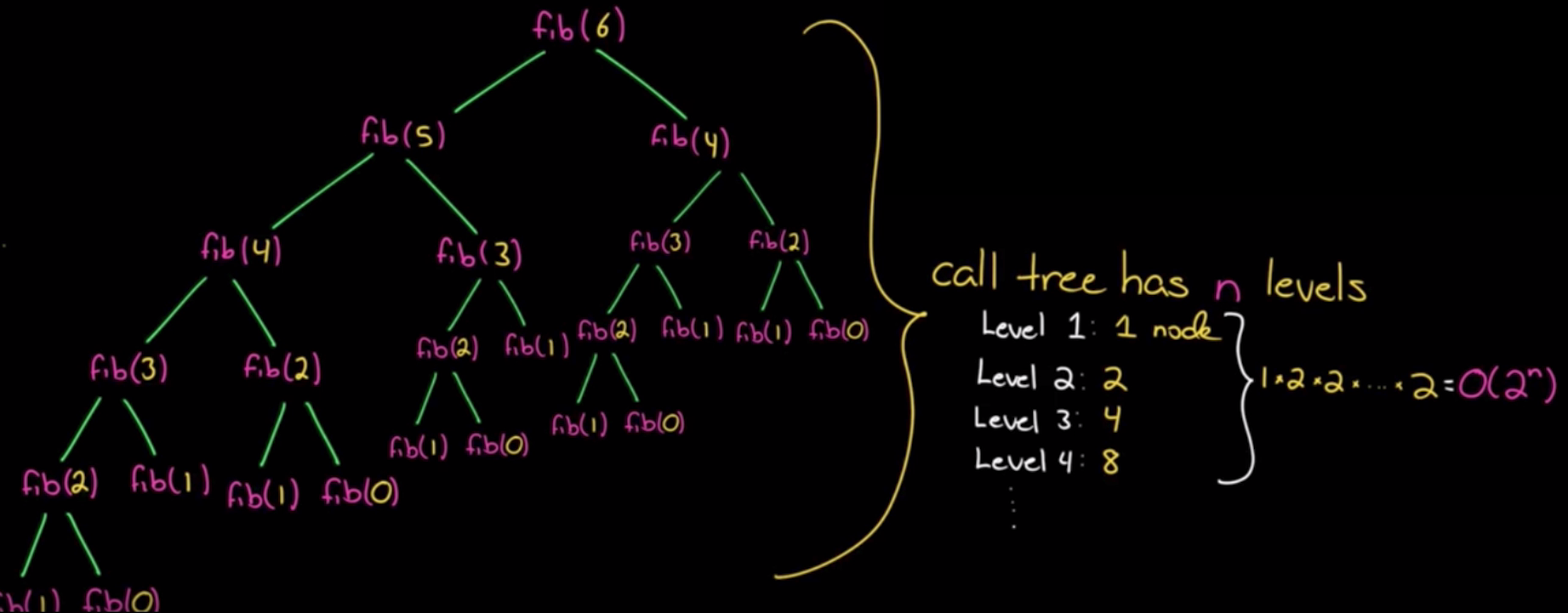
image.png

代码形式如下。

  1. function fib(n) {
  2.     if(n <=0) {
  3.       return 0
  4.   } else if(n == 1) {
  5.       return 1
  6.   } else {
  7.       return fib(n-1) + fib(n-2)
  8.   }
  9. }
  11. // 简化形式如下
  12. function fib(n) {
  13.     return n <= 1 ? n : fib(n-1) + fib(n-2);
  14. }

记忆化

但是从上面也可以看出很多重复计算，比如 fib(4) 被计算了两次，这时我们可以通过记忆化的方式，也就是通过一个数组把结果缓存起来，当有缓存（memo有值）时直接取缓存结果，没有时才去计算。代码如下。

  1. function fib(n, memo = []) {
  2.     if(n <=0) {
  3.       return 0
  4.   } else if(n == 1) {
  5.       return 1
  6.   } else if(memo[n]) {
  7.       memo[n] = fib(n-1) + fib(n-2)
  8.   }
  9.   return memo[n]
  10. }

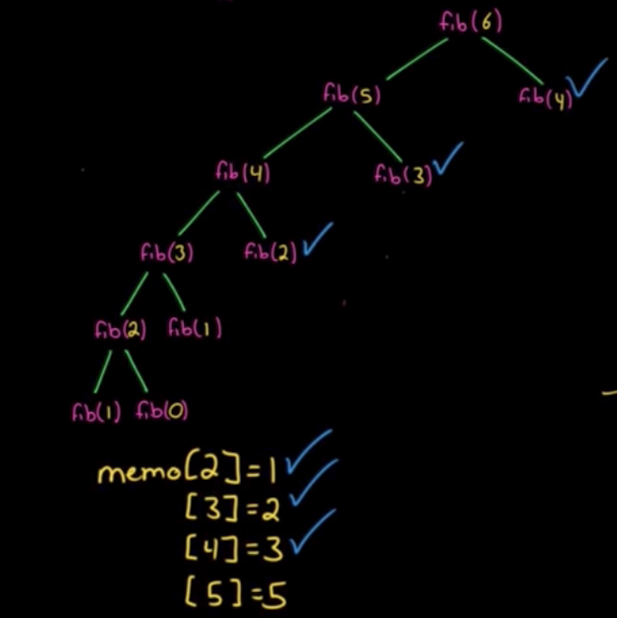
image.png

可以看出，通过这种形式，每个节点只被访问和计算了一次，从而达到时间复杂度优化到了 O(n)。

递推

接着就是把上面的例子转化为递推的形式，这里就不再是自上而下，而是反过来，从下往上计算，因为最下面的值就是初始值（fib[0]=0, fib[1]=1），而我们要做的就是不断的往上加。

它的一个递推公式是 F[n] = F(n-1) + F(n-2)。伪代码如下。

  1. F[0]=0, F[1] = 1
  2. for(var i=2; i<=n; ++i) {
  3.     F[i] = F[i-1] + F[i-2]
  4. }
  6. function fib(n) {
  7.     var memo = [], memo[0]=0, memo[1]=1
  8.   for(var i=2; i<=n; ++i) {
  9.        memo[i] = memo[i-1] + memo[i-2];
  10.   }
  11.   return memo[n]
  12. }