基础知识

数据结构

数据结构可以包括如：排序，二叉树，图论，堆栈，链表等等。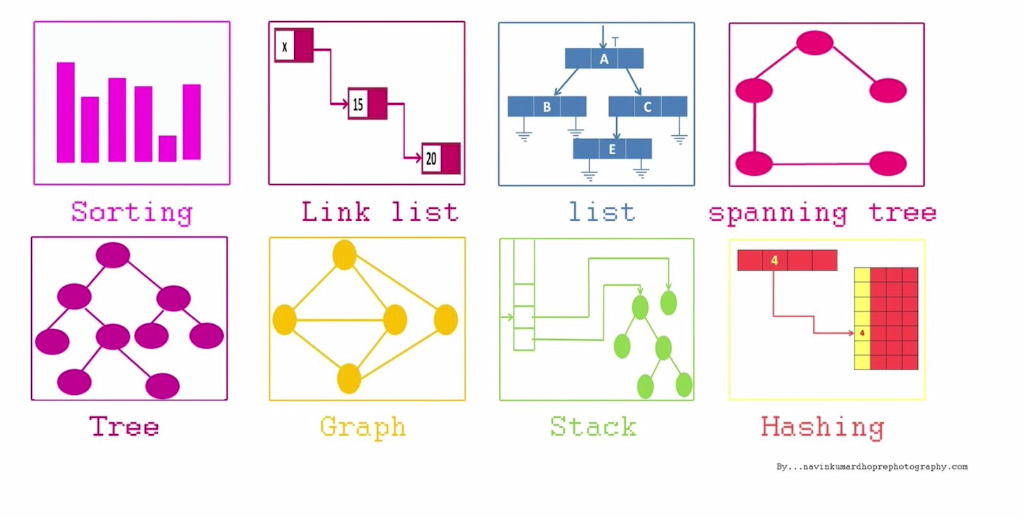

像这样的一个个数据结构都是知识点，在学习这些知识时，要注重他们之间的整体脉络关系。如下图，首先是数据结构，接着分为栈、队、set、map。对于每一块会有相应的细分数据结构。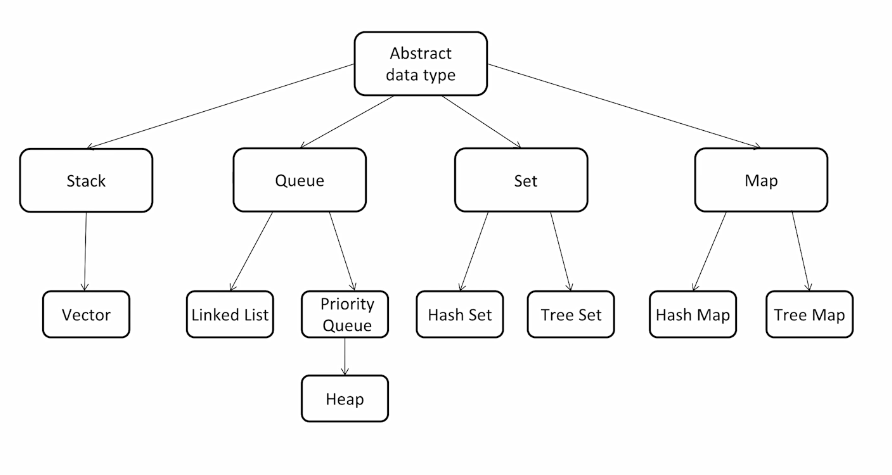

时间复杂度

什么是时间复杂度？

在计算机科学中，算法的时间复杂度（Time complexity）是一个函数，它定性描述该算法的运行时间。 这是一个代表算法输入值的字符串的长度的函数。 时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。 使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。 —-wikipedia

在计算时间复杂度时，我们一般使用大O来表示。使用这种方式来表示时，时间复杂度可被称为是渐近的。只考虑最高时间复杂度的运算，忽略低复杂度的运算（即只考虑输入值大小趋向于无穷大的情况）。例如对于一个数量为n的算法，它至多需要n+2n+1等时间来完成。那么它的渐近时间复杂度是 O(n)。

我们来看一些例子。

对于上面的例子，它们都是O(1)级别的运算。因为虽然n=1000，但其实程序只做了一次输出运算，即常数级的运算。只要是常数级的运算，不管是O(1)，O(2)，O(3)，在复杂度的表示上我们都认为它是O(1)。

而对于上面这个例子，第一个例子程序遍历了n次，第二个例子中程序for循环嵌套了for循环，那么程序的工作量是成平方增长的，所以第一个例子是O(n)，第二个例子是O(n)。

对于其他的例子如下，这里不一一赘述。

我们可以通过一个坐标图来表示。对于同一个程序，如果我们使用时间复杂度越低的算法，当数量级很大时，那么就可以节省计算机运算的细节是很大的。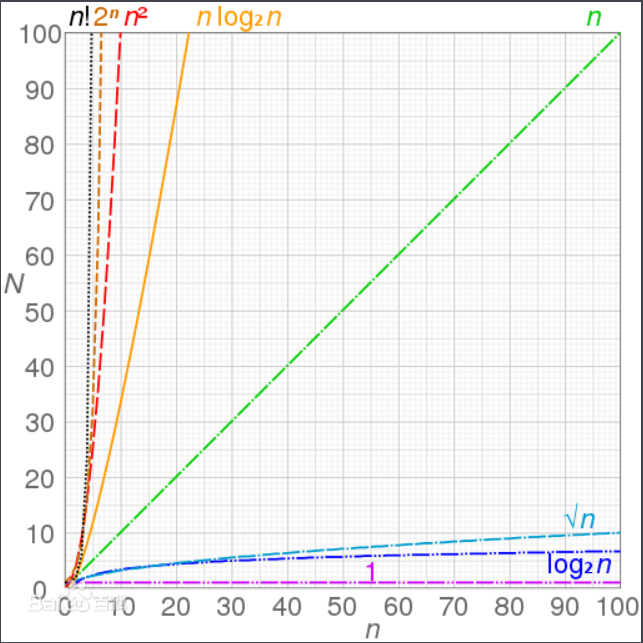

下面是初中数学一个求和的例子。

如果我们通过计算机for循环一次次累加，那么计算机需要计算n次，这个时间复杂度就是O(n)，当n的值很大时，计算机运算的次数就会越大，时间也会越久。
在第二种方法中，我们知道可以使用等差数列求和公式来求得结果，通过这种方式，不管n的值是多大，计算机也只需要运行一次，时间复杂度是O(1)。
可以看到，算法时间复杂度低，程序的执行效率是有所提升的。

附录

这是一个关于不同数据结构的时间复杂度的对比图。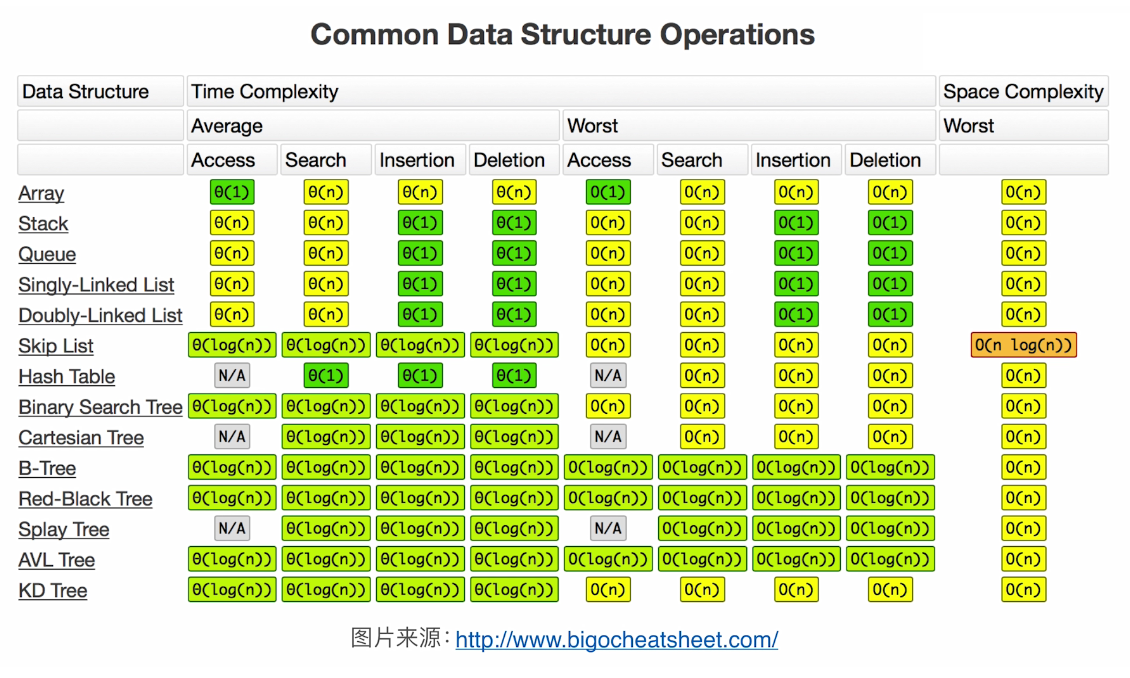

to be continue…