数组
数组是内存连续的一段存储区域。左边是数组的下标,可以通过数组的下标来访问数组元素,右边是数组的内存地址(这里的内存地址只是个示例,并不是在内存中一定是这样)。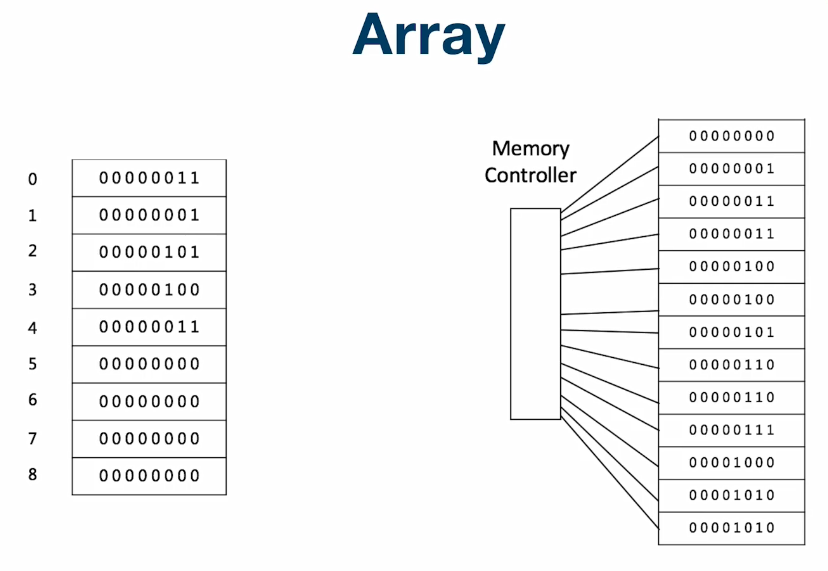
数组通过内存管理器可以随机地访问任意数组元素,计算机只需要进行一次查找就能找到下标相应位置的元素,所以数组访问元素的时间复杂度是O(1)。
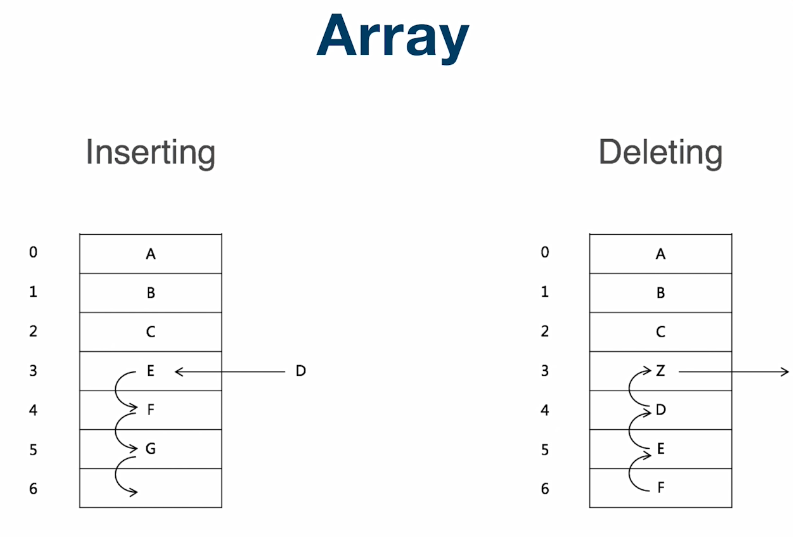
而数组的新增、删除操作则不一样,如右图,我们要给数组插入一个D,那么需要将D插到第三个位置,然后原本的EFG就得依次往后挪动一位(有n个元素挪动n位),删除元素也是类似,所以操作数组的元素的时间复杂度是O(n)。
:::info
提示:为什么插入、删除操作的时间复杂度是O(n)?
如果插入的元素就是最后一位,的确不需要挪动其他元素,它的复杂度是O(1),但如果我们插入的位置是第一位,那么就需要挪动所有元素,所以平均下来就是O(1/2n),一般我们都使用平均值来表示,所以时间复杂度就是O(n)。
:::
所以数组的查询是O(1),但插入、删除是O(n)的,那么我们有没有方法来改善它的插入和删除操作呢?一种新的数据结构就是链表。
链表
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 主要有单链表和双链表。
链表主要应用于两种场景,一种就是插入、删除操作非常多,另一种是你不知道有多少个元素存在,进来一个元素就直接插入到后面去。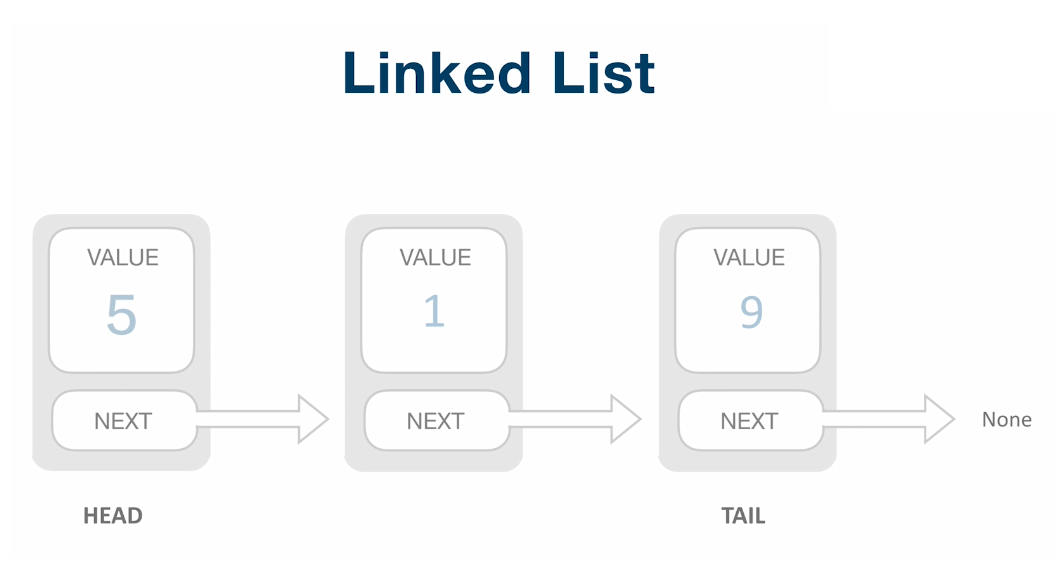

同时还有一种提供了头尾指针的链表,可以方便我们知道头指针和尾指针。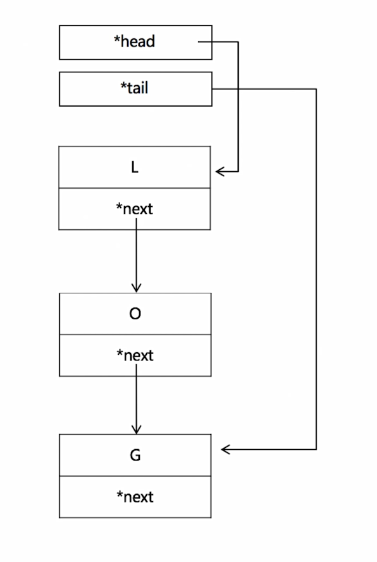
链表的插入、删除操作都比较简单。只要给插入地方的前一个节点next指针指向插入元素,插入元素的next指针指向下一个元素节点就好了。删除同理就是断开节点的连接。这两种操作都是只需要修改2次next指针的指向实现的,它的时间复杂度是O(1)。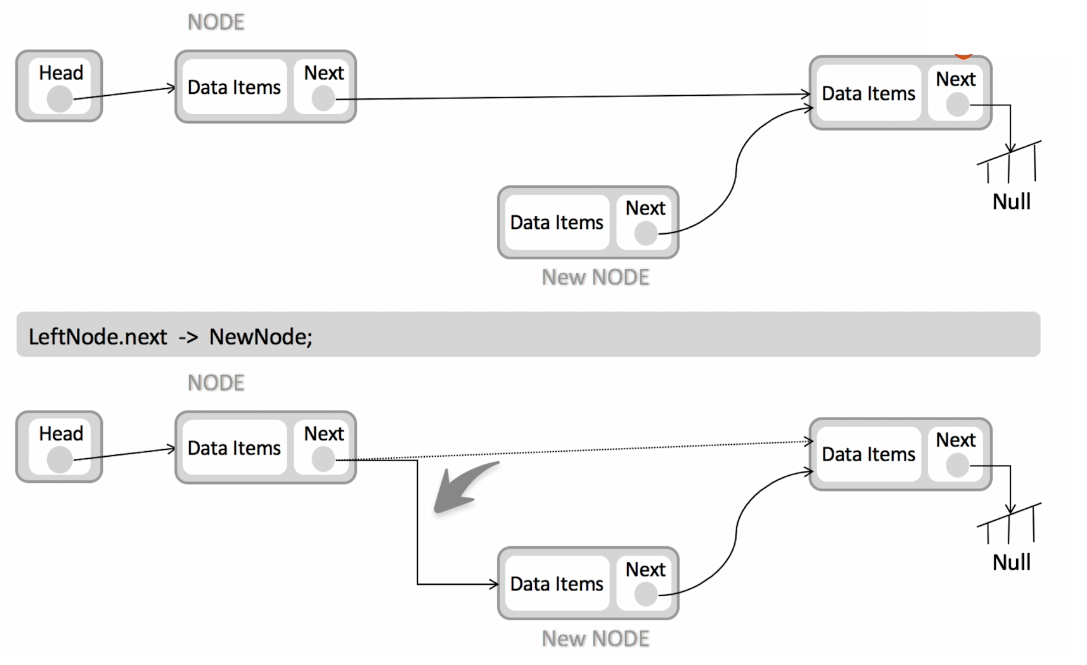
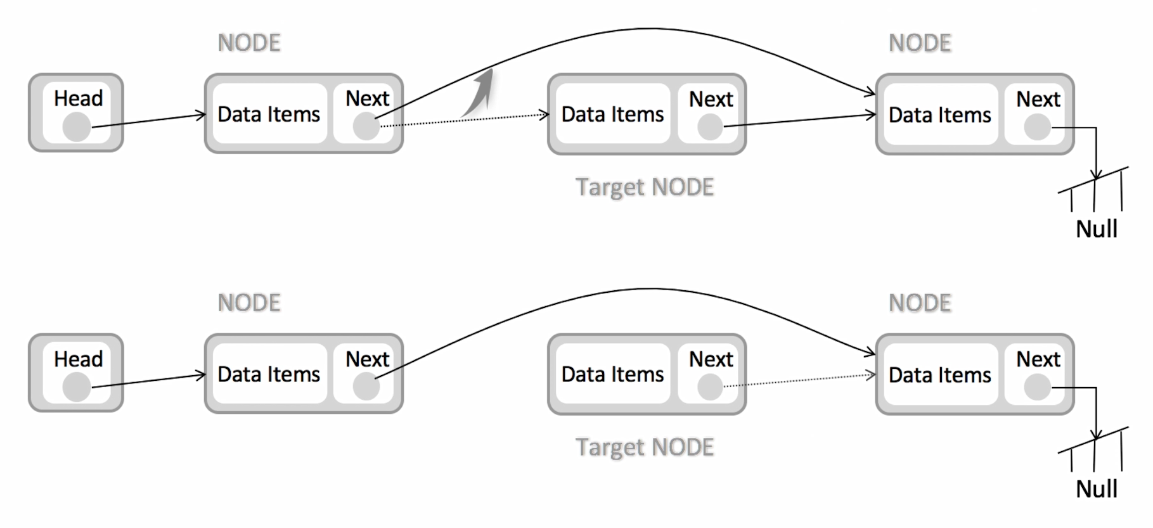
但是如果需要查找到第n个元素的位置,那么就需要挪动n次才能找到,所以查找的时间复杂度是O(n)。
从这里可以看出,数据结构和不同的算法之间是动态平衡的,像数组在查询时比链表快,但插入删除时就比链表要慢。所以在实际应用中,需要根据实际情况选择数据结构,没有一种数据结构是最好的。
总结
- 数组的查询时间复杂度是O(1),插入删除的时间复杂度是O(n);
- 链表的查询时间复杂度是O(n),插入删除的时间复杂度是O(1);
to be continue…

