章节5 多变量线性回归

多特征的描述

采用矩阵的形式来描述多个特征

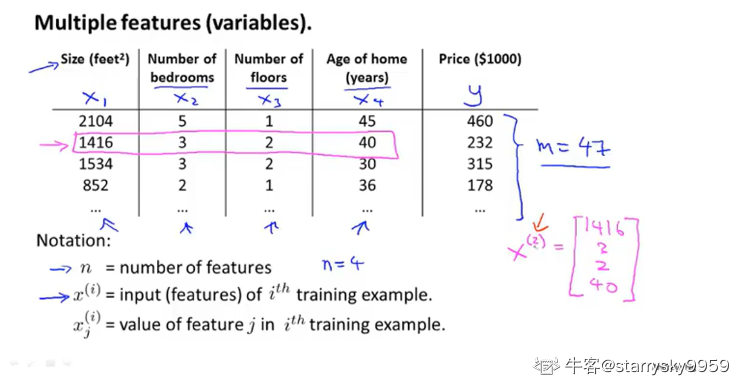
将梯度下降算法从一元或二元推广到多元

特征缩放(Feature Scaling)

作用：确保这些特征在一个相近的范围之内，这样梯度下降算法能够更快地收敛。想象一下使代价函数的等高线更接近圆

• 比例缩放

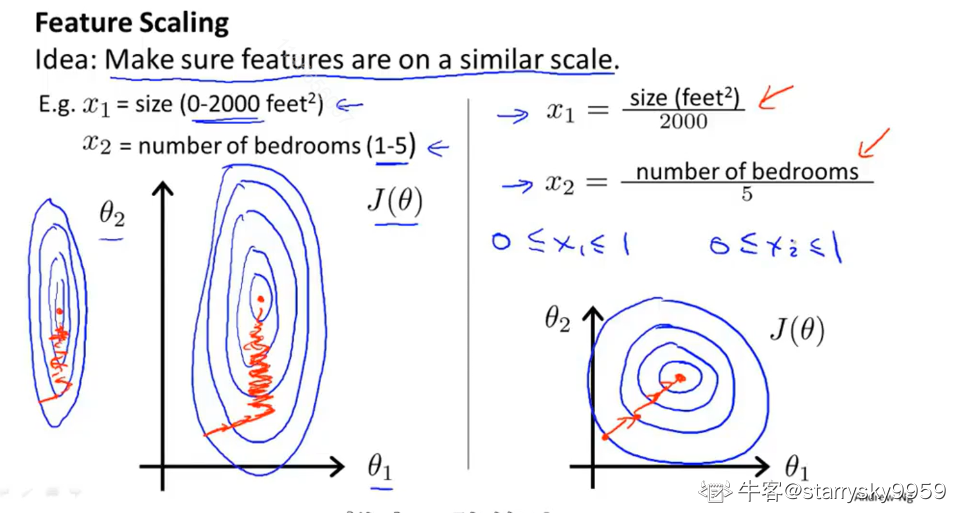
• 归一均值化(Mean normalization)

学习率(Learning rate α)

自动收敛测试：当代价函数 J(θ) 的在某次迭代后的变化小于一个阈值就认为迭代已经充分了。

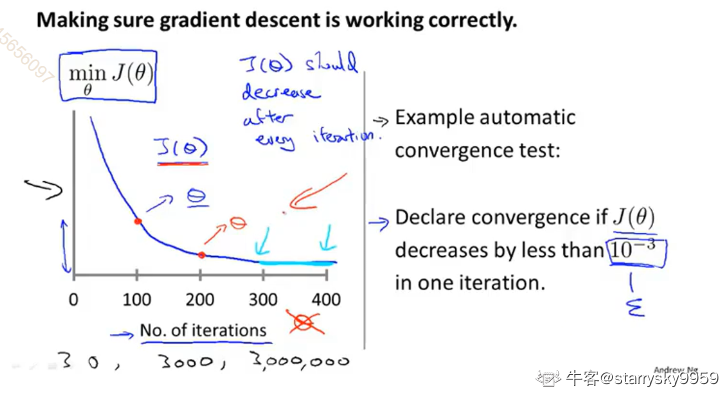
当学习率 α选择过大，可能导致梯度下降算法不能正确进行，无法产生收敛的趋势。

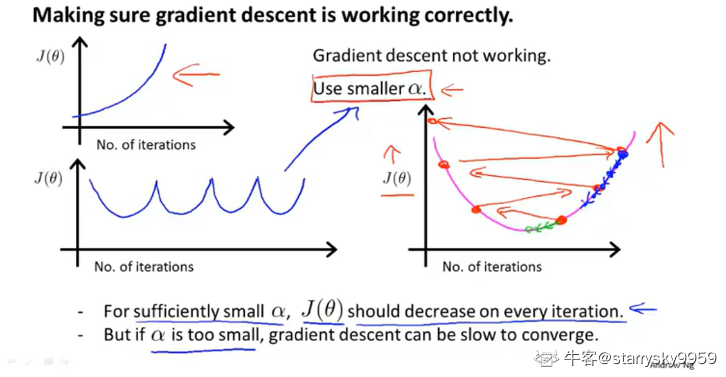
debug 时，绘制代价函数的变化曲线可以帮助你更好地选取学习率 α。

多项式回归(Polynomial regression)

特征的选择是非常灵活的，你可以通过现有的特征来构造新的特征。比如用面积来组合长、宽这两个特征用于描述房子的属性。

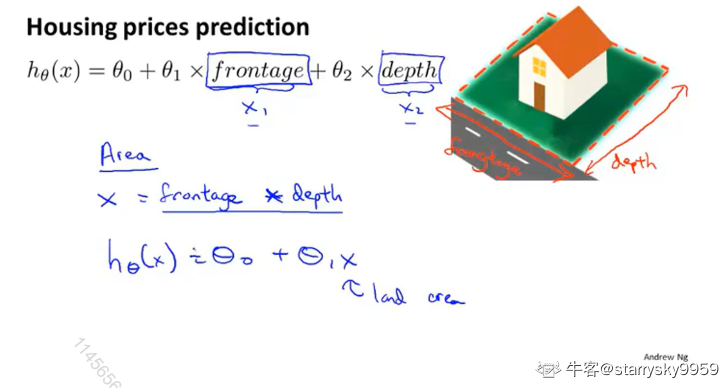
再比如在根据房子面积来预测房价这个模型中，对于面积这个单一特征，用一次多项式或二次多项式的函数去描述都不太合适，你可能需要用到三个变量，那么可以通过图中这种构造方法来创建三个新的特征。此时，特征缩放的用处也体现出来了

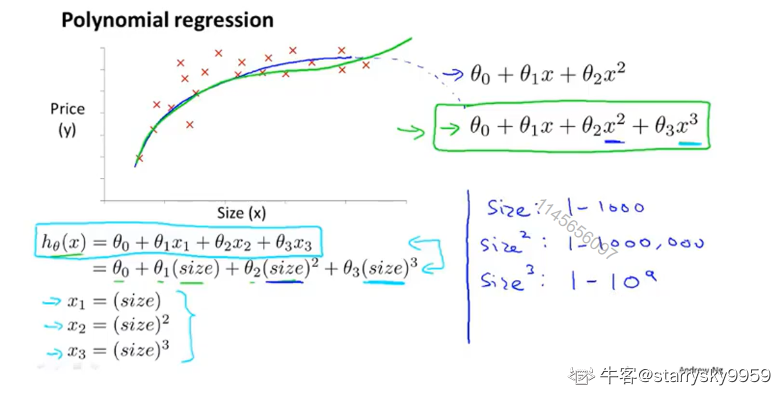
正规方程(Normal equation)

直接求解答案而不是通过多次迭代，即求出当偏导数为 0 时，特征向量 的值

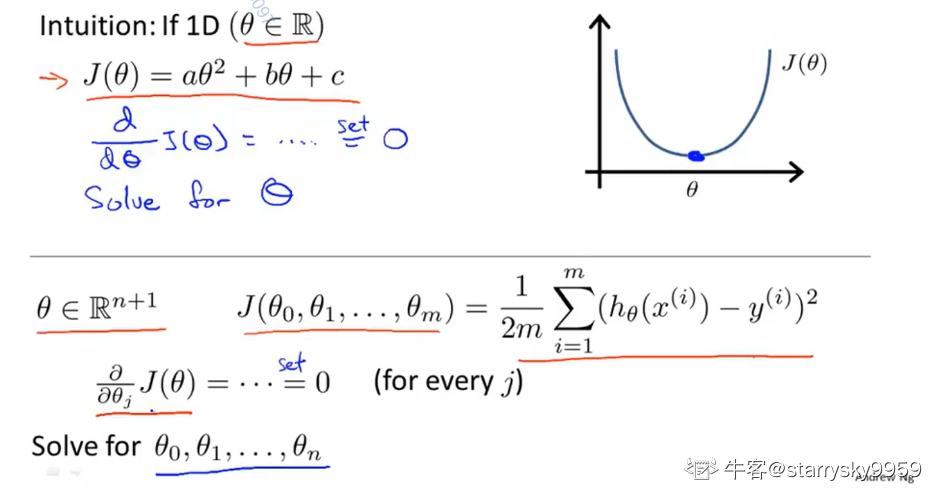
计算方法为

%5E%7B-1%7DX%5E%7BT%7Dy#card=math&code=%5Ctheta%20%3D%20%28X%5E%7BT%7DX%29%5E%7B-1%7DX%5E%7BT%7Dy)

矩阵构造方法如下

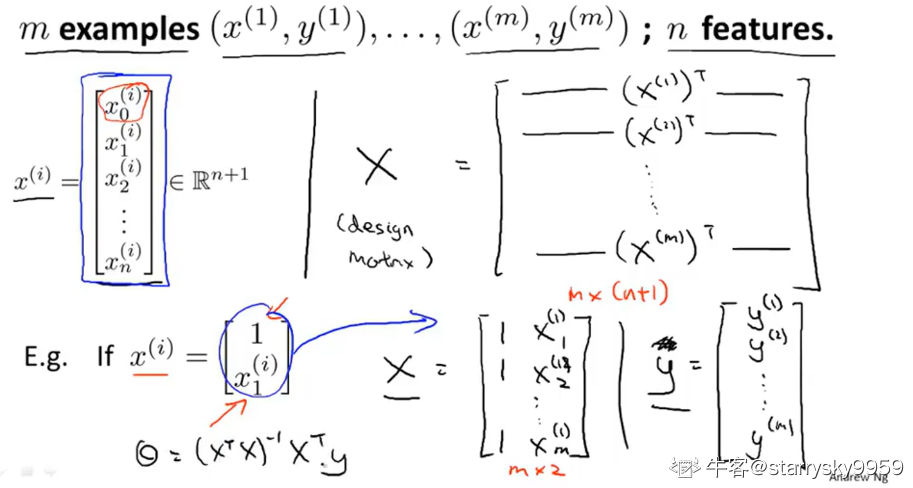
• 如果 不可逆怎么办
  产生该情况可能有以下原因,这些情况在线性代数中关于线性方程的解的相关章节中其实都是讲过的

  1. 使用了多余的特征,即特征向量不是线性独立

     
     
     显然英尺 和 之间是可以直接换算的,那么包含 和 的特征向量一定是线性相关的

  2. 包含了太多的特征,比如满足样本数 m < 特征数 n
     可以使用正规化的方法来纠正

梯度下降和正规方程两者对比

	梯度下降	正规方程
优点	在 n 的规模很大的时候依然表现良好	没有梯度下降这么多麻烦的工作
缺点	需要选择学习率, 需要多次迭代, 这都取决于具体细节, 需要尝试, 并意味着额外的工作和麻烦, 比如画出时代价函数, 判断收敛性	需要计算矩阵的逆和转置以及矩阵乘法, 这个计算量随着 n 的增大而显著升高, 大约%20%3D%20n%5E%7B3%7D#card=math&code=O%28n%29%20%3D%20n%5E%7B3%7D)
适用规模	n>>10000	n<10000