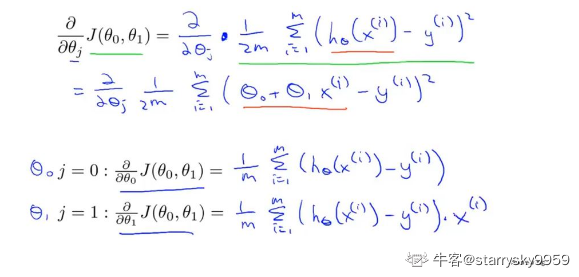章节2 单变量线性回归

单变量线性回归

%20%3D%20%CE%B8_0%20%2B%20%CE%B8_1x#card=math&code=h%28x%29%20%3D%20%CE%B8_0%20%2B%20%CE%B8_1x)

%20%3D%20%5Cfrac%7B1%7D%7B2m%7D*%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7B(h(x_i)-y)%5E2%7D#card=math&code=J%28%5Ctheta_0%2C%20%5Ctheta_1%29%20%3D%20%5Cfrac%7B1%7D%7B2m%7D%2A%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7B%28h%28x_i%29-y%29%5E2%7D)

目标：求解 minisize{#card=math&code=J%28%5Ctheta_0%2C%20%5Ctheta_1%29)}

• 代价函数 #card=math&code=J%28%5Ctheta_0%2C%20%5Ctheta_1%29)
  又称为平方代价函数或平方误差函数。解决回归问题最常用的手段。

简化问题

%20%3D%20%5Ctheta1x#card=math&code=h%28x%29%20%3D%20%5Ctheta_1x)
%20%3D%20%5Cfrac%7B1%7D%7B2m%7D*%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7B(%5Ctheta1x-y)%5E2%7D#card=math&code=J%28%5Ctheta_1%29%20%3D%20%5Cfrac%7B1%7D%7B2m%7D%2A%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7B%28%5Ctheta_1x-y%29%5E2%7D)

通过选取一些离散的 的值我们可以大致画出 和 #card=math&code=J%28%CE%B8_1%29) 之间的关系曲线

学习算法的优化目标就是找到令 #card=math&code=J%28%CE%B8_1%29) 最小的情况， 即图中 的点。对于这组数据集 J(1) 就是我们的目标代价函数。

对于原问题的代价函数，用以下 3D 图和等高线图展示

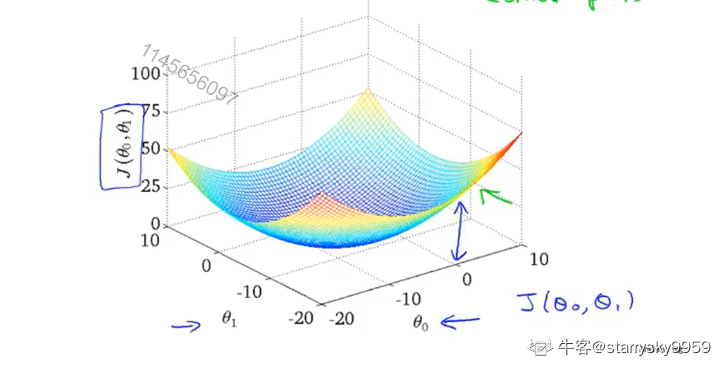
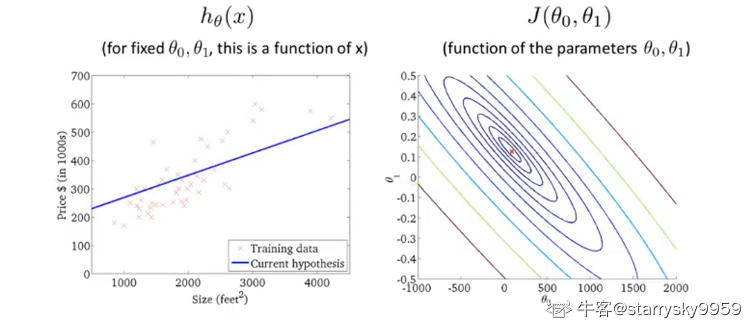
梯度下降

算法梗概

1. 从某个初值出发
2. 朝梯度下降最快的方向更新参数的值，重复此步骤知道达到局部最优解

以下图片展示了梯度下降公式和参数更新的方法

• 说明

要同时更新所有参数，如左侧流程所示。

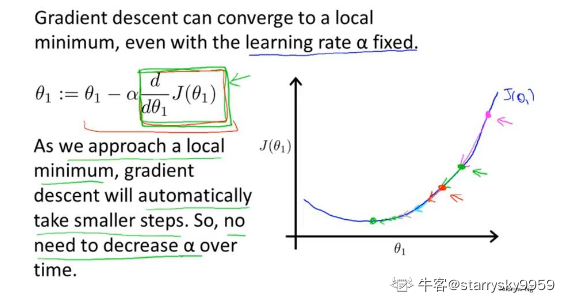
α 表示学习率，即由于控制朝局部最优解更新参数时的步长。α 太小则学习（朝局部最优解优化）的效率过低 ，α 太大则学习时的效率会提高但很有可能在某次更新时错过局部最优解，甚至无法收敛。

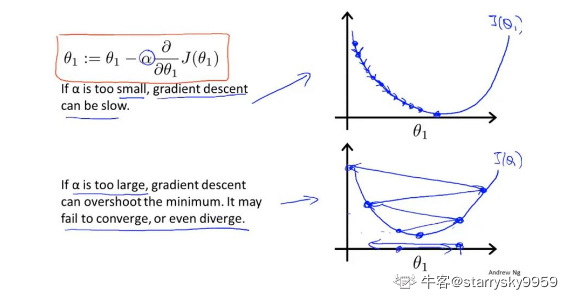
当然，在我们朝局部最优解优化时，梯度下降算法能够自动采取更小的变化幅度来逼近目标。

线性回归的梯度下降

Batch 算法：每一步梯度下降都用全部的数据集

以下为各参数的偏导数