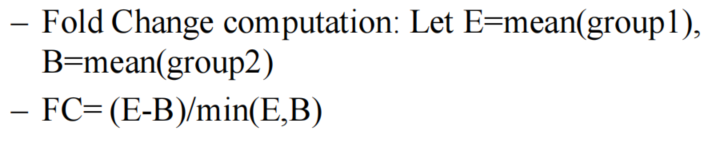- Ⅰ. 基因差异表达
- Ⅱ. 基因富集分析
- Ⅲ 主成分分析
- r:指定输入的数据,如果输入的是原始数据,R将自动计算其相关系数矩阵
- nfactors:指定主成分个数
- residuals:是否显示主成分模型的残差,默认不显示
- rotate:指定模型旋转的方法,默认为最大方差法
- n.obs:如果输入的数据是相关系数矩阵,则必须指定观测样本量
- covar:逻辑参数,如果输入数据为原始数据或方阵(如协方差阵),R将其转为相关系数矩阵
- scores:是否计算主成分得分
- missing:缺失值处理方式,如果scores为TRUE,且missing也为TRUE,缺失值将被中位数或均值替代
- impute:指定缺失值的替代方式,默认为中位数替代;
- method:指定主成分得分的计算方法,默认使用回归方法计算。
- Ⅳ 聚类分析
- 实现层次聚类的hclust()函数
- d:欧式距离矩阵
- method:计算类间距离的方法。”single”(最小距离)、”complete”(最大距离)、”average”(类平均法)、”median”(中间距离法)、”centroid”(重心法)和”ward”(离差平方和法)
- 可视化展示
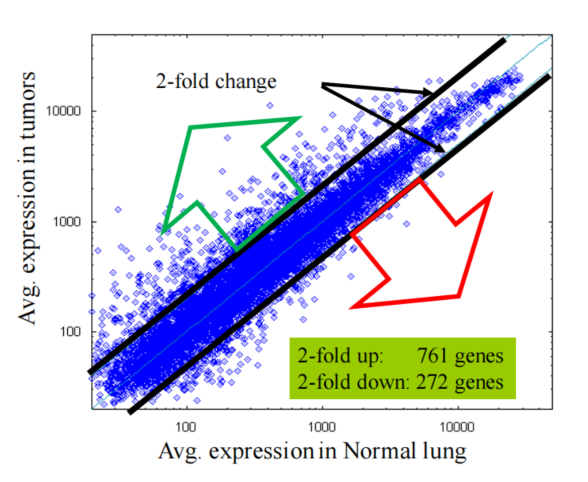
Ⅰ. 基因差异表达
1. Fold Change
1.计算公式
2.fold change cutoffs
3.缺点
- 对一些本底表达很高/很低的基因分析不足
- 不能考虑方差
2. p-value
1.t-test【2个条件下】
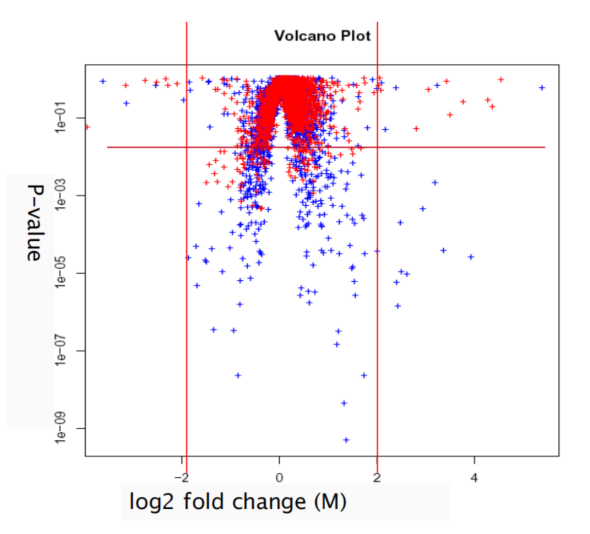
3. 结合p-value和fold-change——火山图
Ⅱ. 基因富集分析
1. 用途
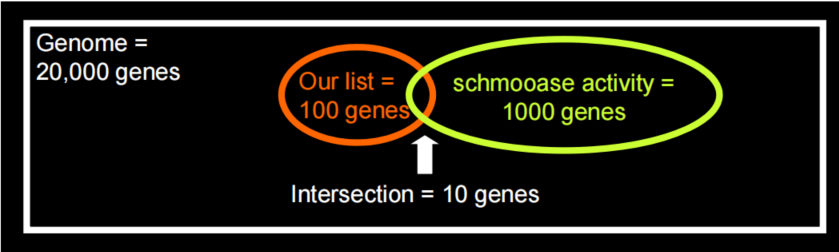
在已经获得了一系列具有差异表达的基因之后,后续希望可以将这些基因进行归类、富集,希望可以找到他们具有的共性(都参与哪一条通路、都具有什么功能等)以及这些基因的差异表达是都是偶然的。
2. 常用的方法
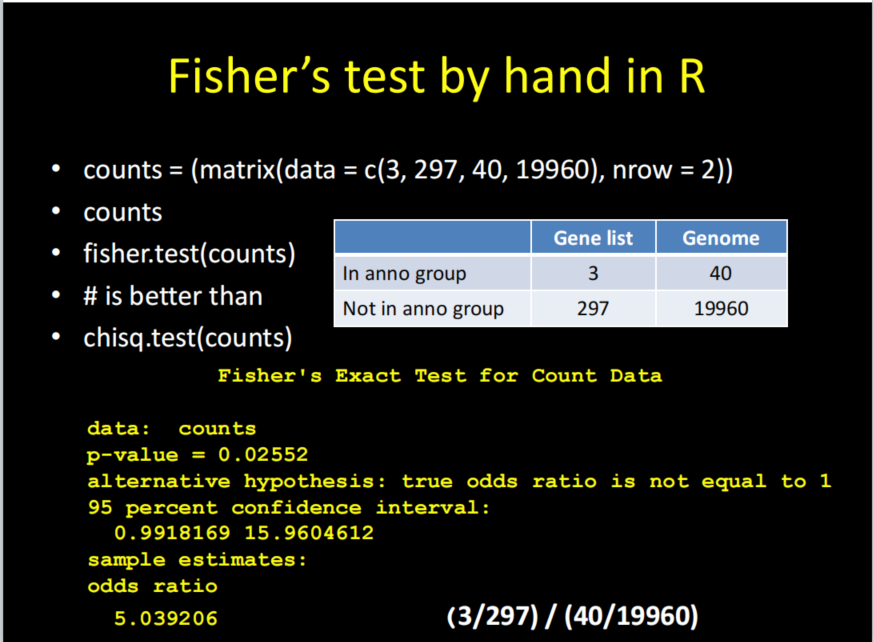
1.Fisher’s test & chi-squzred
2.Hypergeometric

Ⅲ 主成分分析
1. 简介
PCA是一种在损失很少信息的前提下,把多个指标转换为几个综合指标的多元统计分析方法。它的核心是数据降维思想,即通过降维的手段实现多指标向综合指标的转化,而转化后的综合指标,我们将其称为主成分。
其中,每个主成分都是众多原始变量的线性组合,且每个主成分之间互不相关,这使得主成分比原始变量具有某些更为优越的性能。在实际应用中,如果原始数据本身较为复杂,主成分分析不仅可以帮助我们抓住问题的主要矛盾,也能够显著的提高我们的分析效率。
2.原理
3.几何意义
主成分分析的过程就是旋转坐标系,各成分表达式就是新坐标系与原坐标系的转换关系。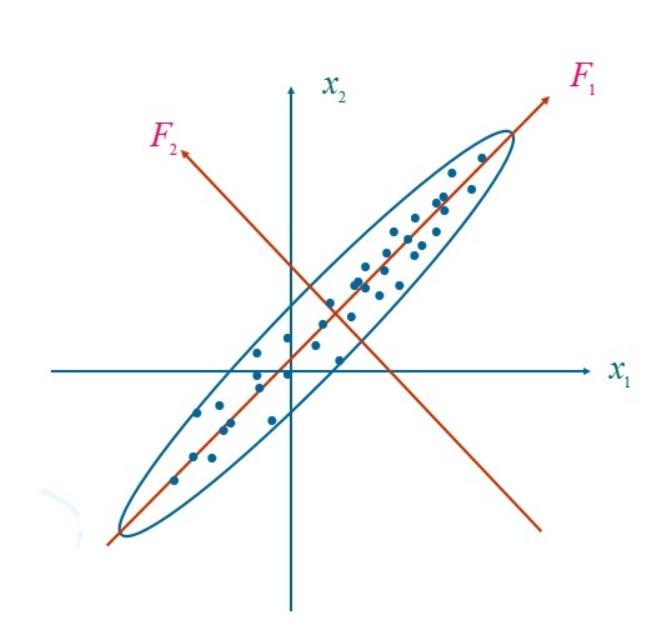
从图中可以看出,变量F1包含了原始变量的绝大多数信息。
4. 计算步骤
对原始数据进行标准化处理,消除量纲→计算标准化数据的相关系数矩阵→计算矩阵的特征根及对应的特征向量→最大的特征根,对应的特征向量为第一主成分的系数,并以此类推→计算累计贡献率,选择恰当的主成分个数→解释主成分,写出前k个主成分的表达式→确定各样本的主成分得分→确定主成分得分的数据,作进一步的统计分析。
5.R中代码
- 基础包中的princomp()函数
- psych包中的principal()函数【功能更多】
```r
principal(r, nfactors = 1, residuals = FALSE, rotate=”varimax”,
- n.obs=NA, covar=FALSE, scores=TRUE,missing=FALSE, impute=”median”,
- oblique.scores=TRUE, method=”regression”,…)
r:指定输入的数据,如果输入的是原始数据,R将自动计算其相关系数矩阵
nfactors:指定主成分个数
residuals:是否显示主成分模型的残差,默认不显示
rotate:指定模型旋转的方法,默认为最大方差法
n.obs:如果输入的数据是相关系数矩阵,则必须指定观测样本量
covar:逻辑参数,如果输入数据为原始数据或方阵(如协方差阵),R将其转为相关系数矩阵
scores:是否计算主成分得分
missing:缺失值处理方式,如果scores为TRUE,且missing也为TRUE,缺失值将被中位数或均值替代
impute:指定缺失值的替代方式,默认为中位数替代;
method:指定主成分得分的计算方法,默认使用回归方法计算。
```
stats包中的prcomp()函数
> prcomp(x, retx = TRUE, center = TRUE, scale. = FALSE,tol = NULL, rank. = NULL, ...)# x:指定输入的数据# retx:是否返回rotates变量# center:变量是否能转换成0# scale.:是否有单位方差
6.结果解读
> data_pca <- principal(data[,-1],nfactors = 2,rotate = "none")> data_pcaPrincipal Components AnalysisCall: principal(r = data[, -1], nfactors = 2, rotate = "none")Standardized loadings (pattern matrix) based upon correlation matrixPC1 PC2 h2 u2 comX1 0.13 0.84 0.72 0.281 1.0X2 0.92 0.33 0.96 0.043 1.3X3 0.81 -0.30 0.75 0.251 1.3X4 0.88 0.32 0.87 0.129 1.3X5 0.60 0.35 0.49 0.512 1.6X6 0.97 0.19 0.97 0.026 1.1X7 0.87 -0.27 0.82 0.177 1.2X8 0.94 -0.19 0.91 0.090 1.1X9 0.31 -0.83 0.79 0.210 1.3X10 0.72 -0.04 0.52 0.480 1.0X11 0.97 0.14 0.97 0.034 1.0X12 0.96 0.22 0.97 0.030 1.1X13 0.94 0.17 0.91 0.087 1.1X14 0.86 0.33 0.85 0.148 1.3X15 0.72 -0.30 0.61 0.390 1.3X16 0.87 -0.43 0.93 0.067 1.5X17 0.71 -0.48 0.73 0.266 1.8PC1 PC2SS loadings 11.11 2.67Proportion Var 0.65 0.16Cumulative Var 0.65 0.81......
PC1与PC2栏为成分载荷,它是指观测变量与主成分的相关系数,从上表中我们可以看到,第一主成分与X2、X4、X6等变量高度相关,第二主成分与X1、X9等变量相关。
- h2栏指成分公因子方差,即主成分对每个变量的方差解释度。对于X2,两个主成分一共解释了96%的方差
- u2栏指成分唯一性,即方差无法被主成分解释的比例(1–h2)。
- SS loadings行包含了与主成分相关联的特征值,指的是与特定主成分相关联的标准化后的方差值。
Proportion Var行表示的是每个主成分对整个数据集的解释程度,在这一案例中,第一主成分解释了65%的方差,第二主成分解释了16%,两者总共解释了81%的方差。
7.绘制主成分分析图
Ⅳ 聚类分析
1.简介
聚类分析的本质是一种数据归约技术,旨在揭露一个数据集中观测值的子集。它可以把大量的观测值归为若干个群组,去组内的观测值相似度要比不同的群之间相似度高。
2.分析步骤
对数据文件进行深入的理解,选择对观测值分组具有重要影响的变量
- 数据的标准化处理,消除量纲的影响
- 搜寻异常值。许多聚类方法对于异常值是十分敏感的,他甚至能扭曲我们的聚类方案。因此,我们需要筛选和删除异常点,或者使用对异常值稳健的聚类方法。
- 距离的计算,这是我们进行分类的判别标准。做常用的是欧几里得距离,还有曼哈顿距离、兰氏距离、非对称二元距离、最大距离等。
- 聚类算法的选择:层次聚类和划分聚类。
- 确定类的数目以及实现算法
- 结果的可视化展示
-
3.计算欧式距离

#准备数据> datat <- iris[1:4]#对数据进行标准化处理> data_scale <-scale(data)#计算距离> data_dist <- dist(data_scale)#格式处理> data_average <- as.matrix(dist_iris)
4.层次聚类分析
每一个观测值自成一类,每次两两合并,直至所有的类被聚到一起。具体算法如下:
定义每个观测值为一类
- 计算每类和其他类的距离【不同算法的主要区别】
- 把距离最短的两类合并成一类,这些类的个数就减少一个
- 重复以上步骤,直到包含所有观测值的类合并成单个的类为止
```r
实现层次聚类的hclust()函数
hclust(d, method = “complete”)
d:欧式距离矩阵
method:计算类间距离的方法。”single”(最小距离)、”complete”(最大距离)、”average”(类平均法)、”median”(中间距离法)、”centroid”(重心法)和”ward”(离差平方和法)
可视化展示
plot(data,hang=-1) ``` 注:高度刻度代表该类合并的判定值。
该方法是贪婪的,一旦一个观测值被分配到一个类中,就不能在后面的过程中重新分配。另外,层次聚类分析难以应用到数百甚至数千观测值的大样本中,而划分聚类则对大样本分析有显著的优势。
5.划分聚类分析
观测值被分为K组,并根据给定的规则改组成具有粘性的类,主要有两种算法:K-means聚类算法和基于中心点的划分。
1.K-means聚类算法
随机选择k个中心点→把每个数据点分配到离它最近的中心点→重新计算每一类中的点到该类中心点的平均值→重新分配→直至所有观测值都不在重新被分配。
#K-means聚类分析> kmeans(data,centers)#center:聚类数目#可视化聚类结果> library(ggfortify)> autoplot(kmeans(data_scale, 3),data=data_scale,label=TRUE, label.size=3, frame=TRUE)
2.围绕中心点的划分
由于K-means聚类方法是基于均值的,所以它对异常值敏感。而PAM法更加的稳健,具体步骤如下:
随机选择k个观测值,且每个都成为中心点→计算每个观测值的到各个中心的距离,即相异型→把每个观测值分配到最近的中心点→计算每个中心点到每个观测值的距离的总和→选择一个该类中不是中心的点,和中心点互换→重新吧每个点分配到据他最近的中心点→再次计算总距离,如果比原本的少,则把新的点作为中心点→重复上述步骤,直至中心点不再改变。
#pan函数> library(cluster)> data_pam <- pam(data_scale,k=3,stand=TRUE)