阅读原文：https://joshualoftus.com/posts/2020-11-23-least-squares-as-springs/

回归的物理直觉和其他最小化平方误差的方法。 我们可以想象弹簧将模型拉向数据。

在最近的“缩放”讲座中，一个学生问我一个关于异常值的问题。 在回答过程中，我意识到我所知道的是真实的，但从未在任何资料中得到解释。 这篇文章是我第一次尝试建立一个将最小二乘法（如回归或PCA）与关于弹簧或弹性的物理直觉联系起来的类比的尝试。
**

最简单的版本

为了说明这一点，我将使用Jenny Bryan在R包中方便地提供的gapminder中的数据。 考虑数据集中的以下两个变量，即人均GDP和预期寿命，在以下标准散点图中绘制：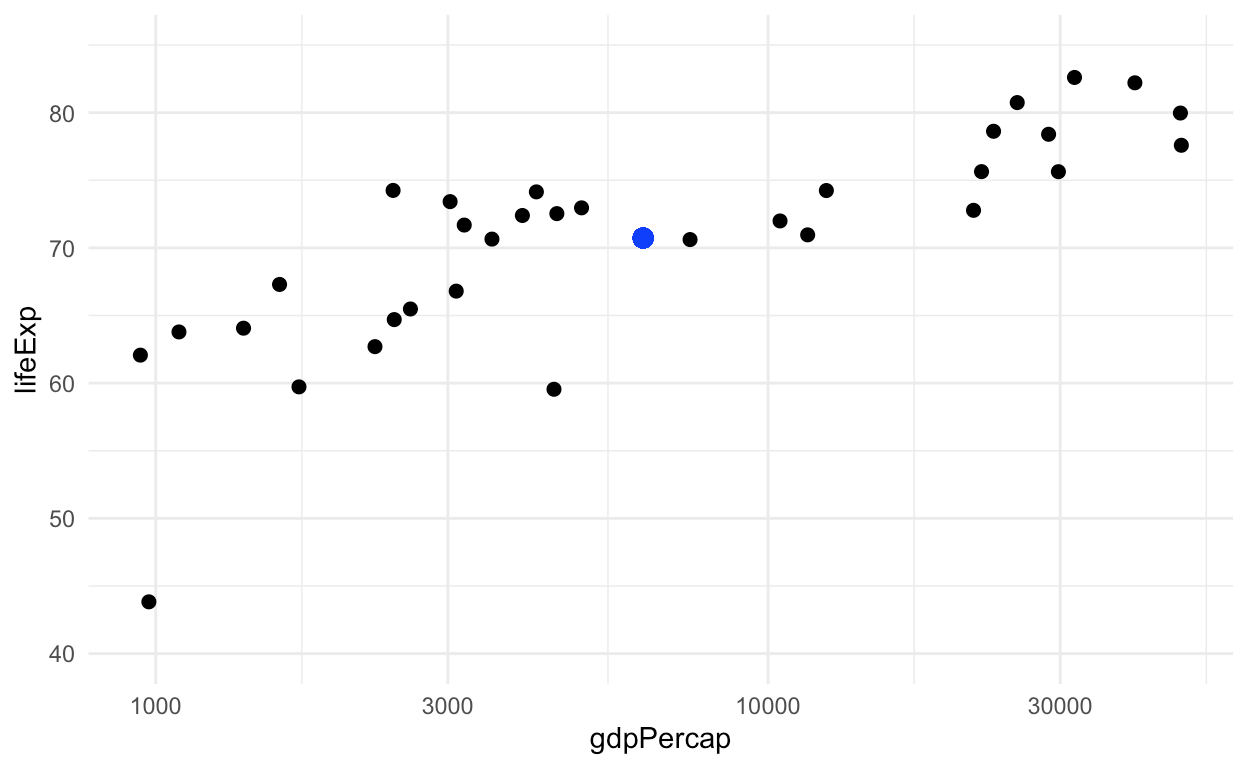
image.png
（为了减少工作量，减少点数，我将数据分为2007年和亚洲国家/地区）。

现在，通过将这些点想象为物理对象，将物理直觉带入其中。例如，我们可以解释【舶来智识】把最小二乘法看作弹簧 - 图2，质心为70.7（如果我们假设每个点的质量都相同）。这是上图中较大的蓝点。专门考虑质量并不是真正重要的事情，只是这一点是身体整体的中心。

对于我们的物理系统，我们需要一些简单的规则：

  • 不允许更改数据，即这些点不可移动。
  • 对于诸如回归（或PCA）之类的方法，我们设想一个刚性物体，如直线（或多重回归中的超平面）穿过这些点，并且这些点施加一定的力来改变该物体的位置。
  • 如果这些方法使用标准的最小二乘损失函数，则该力可以由长度或强度相同的弹簧或弹性表示，它们的一端连接到点，另一端连接到线（或超平面）。

当弹簧将其拉向锚固点时，这条线（或超平面）可能会首先反弹，但最终会稳定下来，平衡所有相对弹簧的力。在这种平衡状态下，我们有两个直接后果：

  1. 刚性物体（直线或超平面）必须穿过中心点。否则，将有一个净力作用在物体上，将其拉向中心点，因此它尚未达到平衡。换句话说，将使物体移动的所有力都被完全平衡，因此它不会移动。
  2. 扭矩也是如此，所有使物体旋转的力都被平衡了。

为了进行回归，我们还需要一条规则：对弹簧进行引导，使其仅沿与结果变量的轴对齐的方向拉动，即“垂直”拉动。我们将此称为垂直规则，以供日后参考。

这是图片形式的简单示例：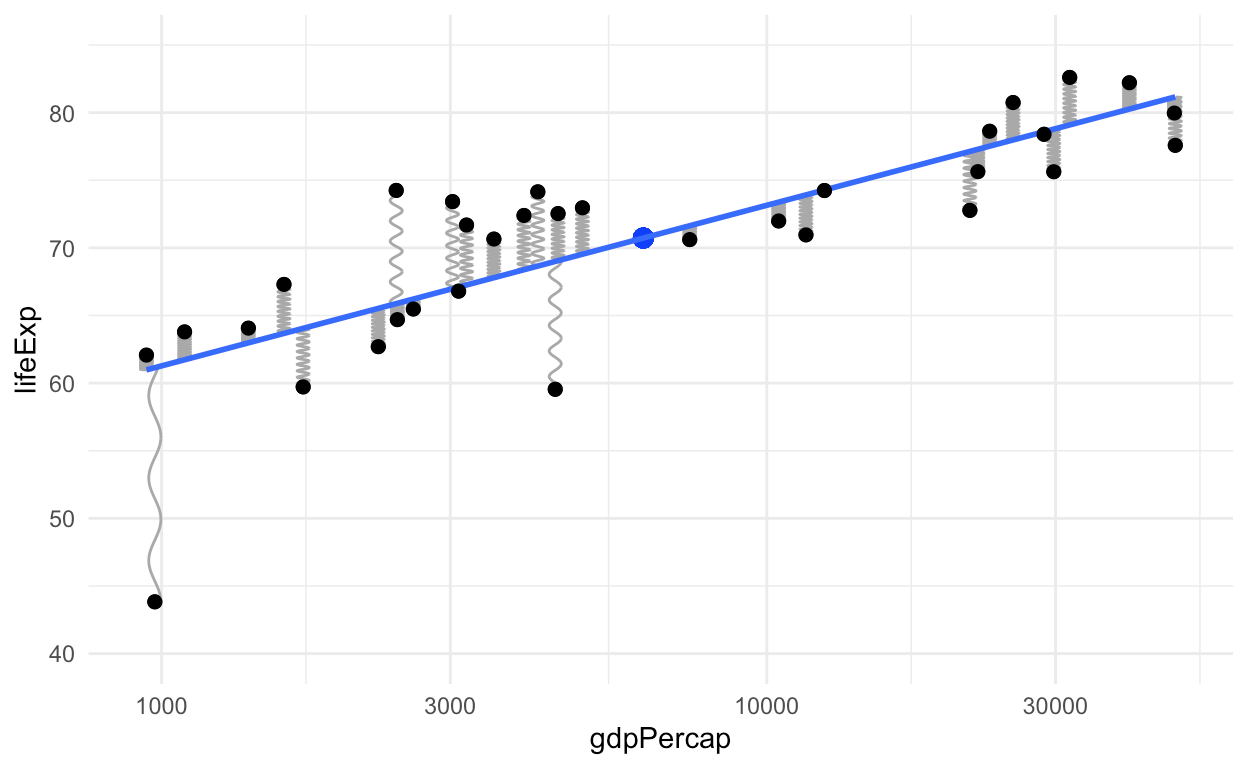
image.png
（为创建此图，我从ggplot2书的新版本中复制了Thomas Lin Pedersen的geom_spring示例）。

如果您不立即相信这种直觉会有所回报，请考虑一下促使我首先想到这一点的问题：有影响力的离群值，即在统计意义上具有较高“杠杆”的点。统计杠杆的定义有点复杂。但是我们可以从物理意义上而不是从那些正式定义中获得正确的直觉。看到上方图表左下方的点了吗？由于它越来越接近线的末端，因此在实际的物理意义上具有更大的杠杆作用。这是我更愿意为没有参加数学统计学课程的学生的解释。

让我们看看移动这一点会发生什么，以便利用其杠杆作用来顺时针旋转线，而不是逆时针旋转线。进行此更改之前，旧的回归线显示为下方的淡色线，以进行比较。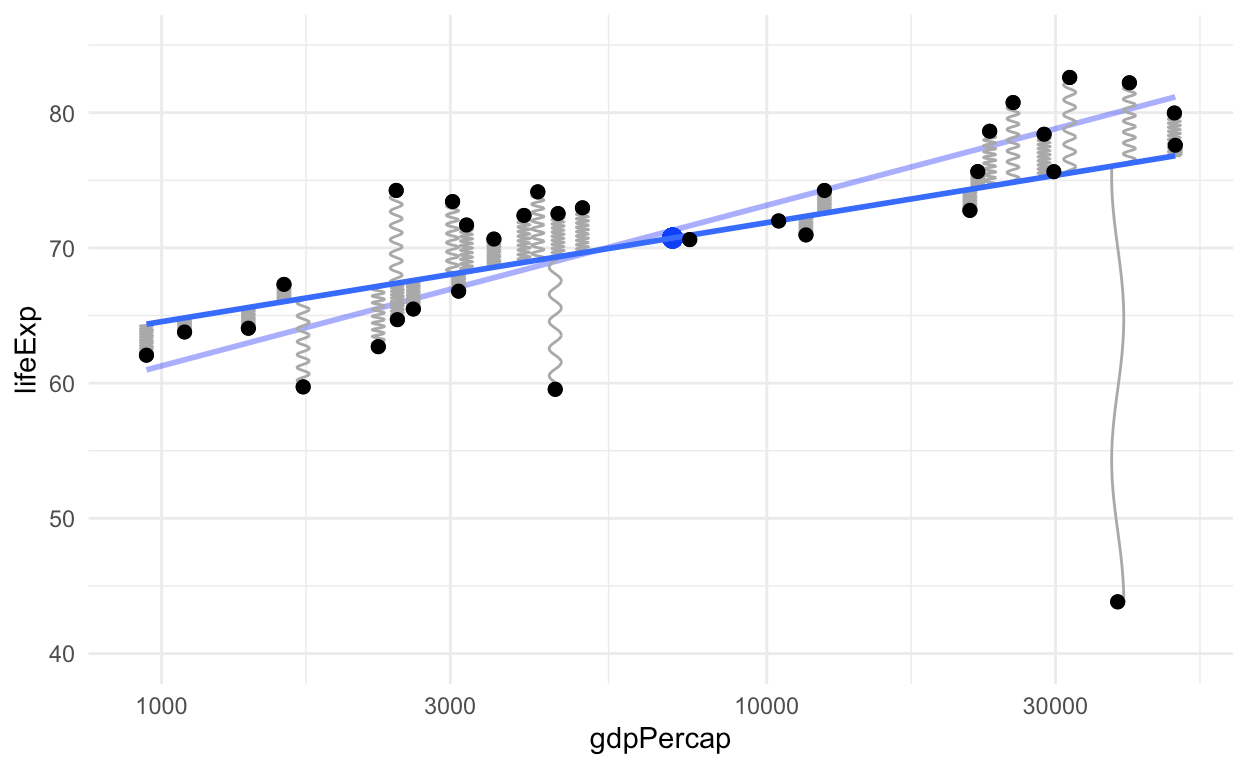
image.png
请注意以下变化：质心稍微移动了一点，我们移动的点现在与直线的距离更大，因此其力更大，并且由于这一点的影响，直线已经明显旋转，即使我们 数据集有30多个点，因为该点具有很大的影响力。

胡克定律

这种直觉正确吗？我们是否真的可以将最小二乘解（例如回归线）视为弹簧系统的平衡？是的，或者是橡皮筋或任何具有线性弹性的材料，即遵循胡克定律的材料。让我们考虑如何将其应用于回归，其中每个点【舶来智识】把最小二乘法看作弹簧 - 图5在数据中，弹簧附加到点【舶来智识】把最小二乘法看作弹簧 - 图6上的回归线。因此弹簧被拉伸到【舶来智识】把最小二乘法看作弹簧 - 图7的长度。胡克定律说，每个弹簧都以与该距离成比例的力拉动绳索。

当管路和弹簧的系统停止移动并达到平衡状态时，此平衡位置会最小化系统的能量，在这种情况下，这只是势能。弹簧中存储的被拉伸一定距离的势能是该距离上力的积分，并且由于力与距离成比例，因此这意味着能量与距离成平方。因此，该物理系统的平衡使总势能最小化：
【舶来智识】把最小二乘法看作弹簧 - 图8
【舶来智识】把最小二乘法看作弹簧 - 图9且是弹簧的“刚度”常数。最小化这一点的线与最小二乘回归线相同，因为前面的常量不会更改最小化器。即使我们无法可视化所涉及的高维图，此参数对于多元回归和简单回归同样有效。我们仍然可以想到垂直于y的弹簧y轴，在超平面上。在这种情况下，各种不同的超平面可能会通过质心传递扭矩，但是它们都被平衡了，因此超平面不会在任何方向上“倾斜”（如果处于平衡状态）。

主成分分析 PCA

尽管PCA通常被认为比（简单）回归更高级，但在我们的物理类比中，其理由实际上更简单。 我们需要做的就是删除回归所需的垂直规则。在这种情况下，允许弹簧旋转其离开点的角度，并且弹簧与线（或超平面）的连接位置可以滑动以适应这种角度变化。 这导致弹簧尽可能少地伸展的平衡。 总势能达到一个较低的值，因为弹簧不再受弹簧可以拉动的方向的限制。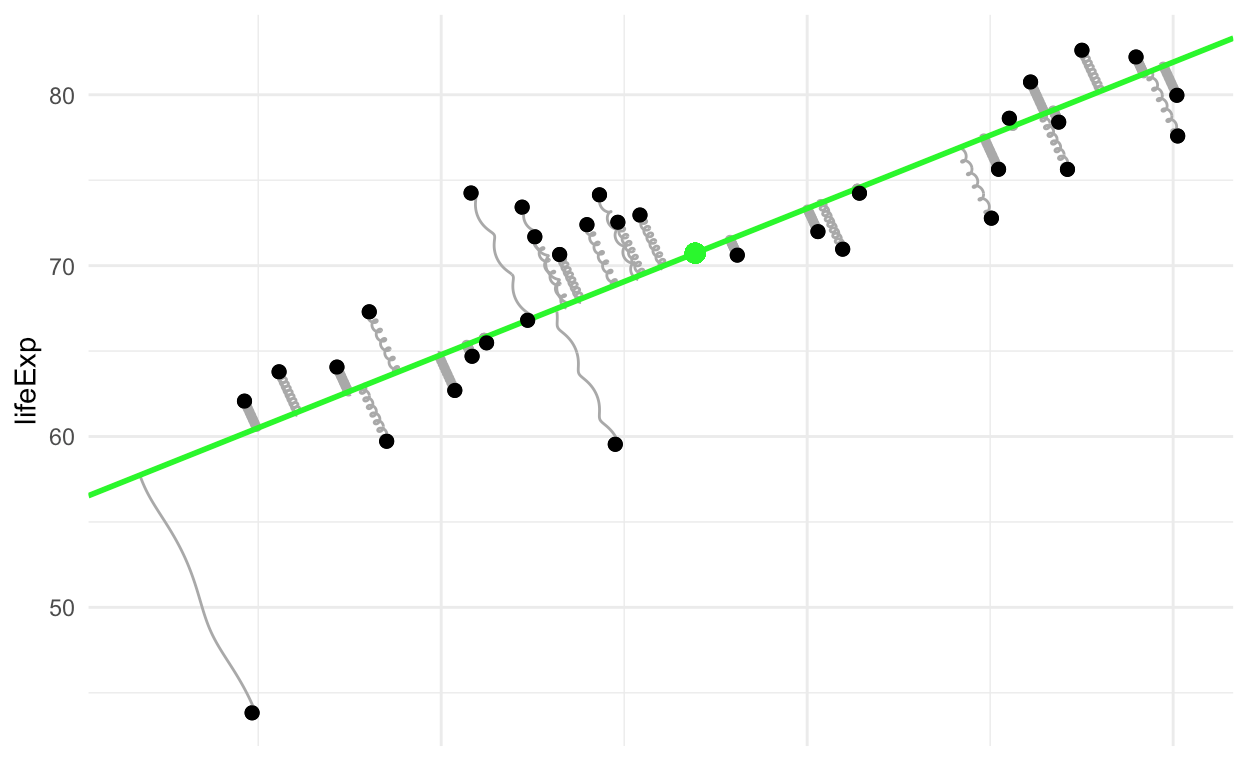
image.png
我用另一种颜色绘制了线条，以强调它不是回归线。请注意，弹簧不再垂直拉动，而是在最接近的线上的点处连接到该线上（按总距离测量，而不仅仅是y轴中的距离）。
（这也称为总最小二乘法或戴明回归的特殊情况。）

模型的复杂性/弹性：机器学习或AI

我们可以通过使用一个比喻来理解更复杂的建模方法，并通过另一个非常简单的想法继续建立这种比喻：模型对象本身的弹性。如果我们想象它是由可以（局部）拉伸和变形的弹性材料制成，而不是像线（或超平面）那样的刚体，那么我们可以获得更复杂类型的回归模型。

在这种比喻中，线性回归等较简单的模型对应于诸如不可弯曲的金属棒之类的刚性物体，而更复杂的模型在拟合条件期望函数（如可弯曲的塑料棒，橡皮筋甚至是无张力的弦）时具有柔韧性或弹性。 在最复杂的情况下，允许模型完美拟合点。

例如，下面是ggplot函数stat_smooth中默认使用的局部多项式回归方法（loess）：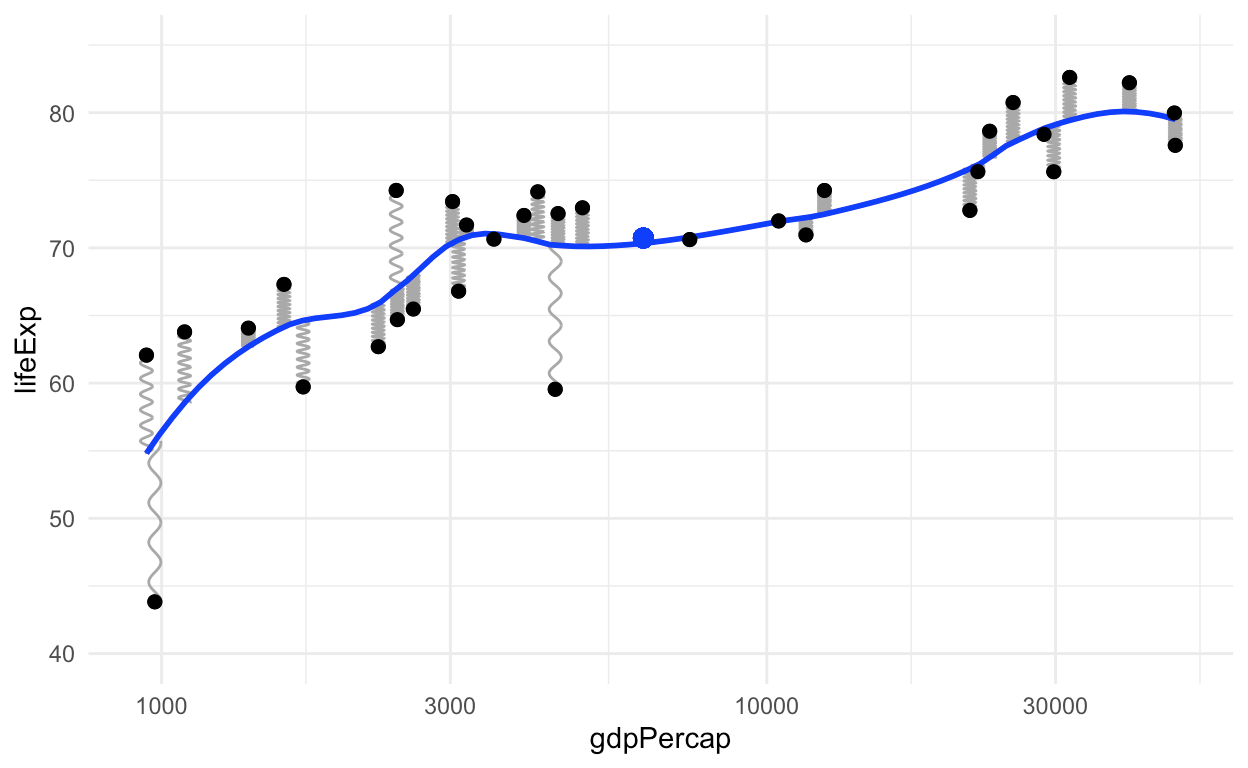
image.png
这种直觉不仅对学习模型复杂性和机器学习的基本思想很有用，甚至可以用于前沿研究。 例如，请参阅最近有关神经网络弹性的论文（由Weijie Su和他的合著者撰写！）

结论思想

我认为这里的统计学教育潜力很大，尤其是对于年轻的学生。 使用弹簧或松紧带进行物理教室演示并不难，尤其是对于PCA案例，因为这不需要任何引导轨道即可将力的方向限制为垂直。

参考

很难找到这个基本概念的参考文献，因为它为最小二乘回归这样的重要方法提供了物理直觉，这让我感到惊讶。 如果您知道其他任何人，请与我联系，因为我很高兴认识他们。

（更新）值得庆幸的是，在Twitter上广泛分享此帖子之后，人们帮助我警惕了更多引用，这些引用现在已包含在下面的列表中。