- 首先准备数据,用的是R自带数据attitude:
- 在做相关性分析之前首先要确定应该使用Pearson还是Spearman相关性分析方法,所以我们先查看数据是否符合正太分布,然后观测有无离群值。
- 通过shapiro.test检验结果p值都>0.01,则不能拒绝原假设,即这7个变量都符合正太分布。
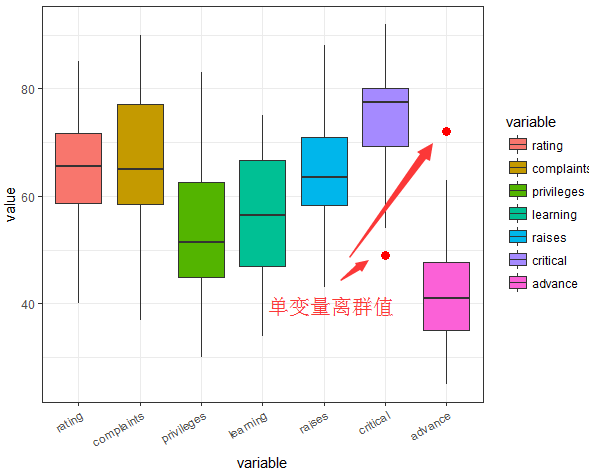
- 接下来做箱线图看看变量是否有离群值:
- 从上图我们发现仅有两个变量中存在离群点,其他变量中并没有离群点存在。有多变量的情况下,我们计算
cook距离衡量某个单变量中离群点在所有变量拟合过程中产生的影响。从几何角度看,Cook距离度量的是使用第i个观测值计算的拟合值与不使用第i个观测值计算的似合值之间的距离。一般来说,如果某个观测的Cook距离比平均距离大4倍,我们就可以认为这个点是离群点。 - 从图中可以看出每个变量中都存在对于拟合结果影响较大(cook距离大于平均距离的四倍)的值,如果我们想综合考虑在这些变量群体中哪个点的影响最大,则可以使用
car包的outlierTest函数: outlierTest结果显示第二个点对于拟合结果的影响最大且具有显著性意义(p<0.01)。如果需要做回归则需要对离群值和异常值进行处理,但在这里我们只需知道存在对于数据拟合结果有显著性影响的异常值,且前面cook距离计算结果显示每个变量都存在离群点。(outliers也提供了检测离群值的outliers函数和scores函数。)- 综上所述,attitude数据集的变量都符合正太分布,cook距离结果表明每个变量都存在离群值,所以我们使用
Spearman相关性系数来计算这个数据集的相关性矩阵。
上期我们介绍了双变量相关性作图(点击查看上期),这期我们来实现相关性矩阵。
首先准备数据,用的是R自带数据attitude:
# 格式化环境:rm(list=ls())# 加载数据:data(attitude)# 预览数据:head(attitude)
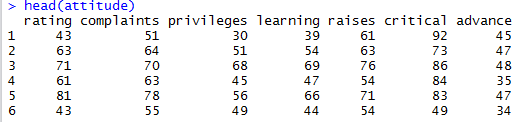
在做相关性分析之前首先要确定应该使用Pearson还是Spearman相关性分析方法,所以我们先查看数据是否符合正太分布,然后观测有无离群值。
for(i in 1:ncol(attitude)){# 使用shapiro.test函数检验每个变量是否与正太分布具有显著性差异p_value <- apply(attitude,2,shapiro.test)[[i]]$p.value# 输出结果变量名和p值。print(paste(names(attitude)[i],p_value,sep=" "))}
通过shapiro.test检验结果p值都>0.01,则不能拒绝原假设,即这7个变量都符合正太分布。
接下来做箱线图看看变量是否有离群值:
library(reshape)library(ggplot2)# 宽格式变为长格式:attitude_melt <- melt(attitude)# 作图查看每个变量的离群值:ggplot(attitude_melt)+geom_boxplot(aes(x=variable,y=value,fill=variable),outlier.colour = "red",outlier.size = 3)+theme_bw()+theme(axis.text.x = element_text(angle = 30,hjust=1,vjust=1))
从上图我们发现仅有两个变量中存在离群点,其他变量中并没有离群点存在。有多变量的情况下,我们计算cook距离衡量某个单变量中离群点在所有变量拟合过程中产生的影响。从几何角度看,Cook距离度量的是使用第i个观测值计算的拟合值与不使用第i个观测值计算的似合值之间的距离。一般来说,如果某个观测的Cook距离比平均距离大4倍,我们就可以认为这个点是离群点。
# 构建函数cook_plot寻找并可视化每个变量的cook距离。cook_plot<-function(attitude_col){# 建立线性模型mod <- lm(eval(parse(text = attitude_col)) ~ ., data=attitude)# 计算cook距离cooksd = cooks.distance(mod)# 构建作图所需数据框:cooksd_d <- data.frame(ID=names(cooks.distance(mod)),cooksd_distance = cooks.distance(mod))# 获得离群点:outline_point <- as.numeric(ifelse(cooksd>4*mean(cooksd_d$cooksd, na.rm=T),cooksd,""))outline_point[is.na(outline_point)]<-0# 作图:ggplot(cooksd_d)+geom_point(aes(x=ID,y=cooksd_distance))+geom_hline(yintercept=4*mean(cooksd, na.rm=T),color = "red")+theme_bw()+ylab(attitude_col)+theme()+annotate("text",x=names(cooksd),y=as.numeric(cooksd),label=ifelse(cooksd>4*mean(cooksd_d$cooksd, na.rm=T),"outlier",""),vjust=1,color="red")}# 调用函数生成每个变量的cooksd值:datalist_p <- lapply(names(attitude),cook_plot)# 批量显示图片:install.packages("cowplot")library(cowplot)# 调用cowplot包的plot_grid函数同时显示多个图:plot_grid(plotlist = datalist_p,nrow=4)
从图中可以看出每个变量中都存在对于拟合结果影响较大(cook距离大于平均距离的四倍)的值,如果我们想综合考虑在这些变量群体中哪个点的影响最大,则可以使用car包的outlierTest函数:
install.packages("car")library(car)car::outlierTest(mod)
outlierTest结果显示第二个点对于拟合结果的影响最大且具有显著性意义(p<0.01)。如果需要做回归则需要对离群值和异常值进行处理,但在这里我们只需知道存在对于数据拟合结果有显著性影响的异常值,且前面cook距离计算结果显示每个变量都存在离群点。(outliers也提供了检测离群值的outliers函数和scores函数。)
综上所述,attitude数据集的变量都符合正太分布,cook距离结果表明每个变量都存在离群值,所以我们使用
Spearman相关性系数来计算这个数据集的相关性矩阵。