介绍
FlinkML旨在使您的数据学习成为一个直接的过程,从而消除了大数据学习任务通常带来的复杂性。在本快速入门指南中,我们将展示使用FlinkML解决简单监督学习问题是多么容易。但首先是一些基础知识,如果您已经熟悉机器学习(ML),可以跳过接下来的几行。
正如Murphy [1]所定义的那样,ML涉及检测数据中的模式,并使用这些学习模式来预测未来。我们可以将大多数ML算法分为两大类:监督和非监督学习。
监督学习涉及学习从一组输入(特征)到一组输出的函数(映射)。使用我们用来近似映射函数的(输入,输出)对训练集来完成学习。监督学习问题进一步分为分类和回归问题。在分类问题中,我们尝试预测示例所属的类,例如用户是否要点击广告。另一方面,回归问题是关于预测(实际)数值,通常称为因变量,例如明天的温度。
无监督学习涉及发现数据中的模式和规律。这方面的一个例子是聚类,我们尝试从描述性特征中发现数据的分组。无监督学习也可用于特征选择,例如通过主成分分析。
与FlinkML链接
要在项目中使用FlinkML,首先必须 设置Flink程序。接下来,您必须将FlinkML依赖项添加到项目的依赖项中pom.xml:
<dependency><groupId>org.apache.flink</groupId><artifactId>flink-ml_2.11</artifactId><version>1.7-SNAPSHOT</version></dependency>
加载数据中
要加载要与FlinkML一起使用的数据,我们可以使用Flink的ETL函数,或者使用格式化数据的专用函数,例如LibSVM格式。对于监督学习问题,通常使用LabeledVector该类来表示(label, features)示例。一个LabeledVector 对象将具有FlinkML Vector表示实施例的特征部件和Double 其代表的标签,其可以是在一个分类问题的类,或用于回归问题因变量构件。
例如,我们可以使用Haberman的生存数据集,您可以 从UCI ML存储库下载。该数据集“包含对接受过乳腺癌手术的患者的生存进行的研究的病例”。数据以逗号分隔的文件形式出现,其中前3列是特征,最后一列是类,第4列表示患者是否存活了5年或更长时间(标签1),或者是否在5年内死亡(标签) 2)。您可以查看UCI页面以获取有关数据的更多信息。
我们可以先加载数据DataSet[String]:
import org.apache.flink.api.scala._val env = ExecutionEnvironment.getExecutionEnvironmentval survival = env.readCsvFile[(String, String, String, String)](docs_1.7-SNAPSHOT_"_path_to_haberman.data")
我们现在可以将数据转换为DataSet[LabeledVector]。这将允许我们将数据集与FlinkML分类算法一起使用。我们知道数据集的第4个数据元是类标签,其余的是函数,所以我们可以构建如下的LabeledVector数据元:
import org.apache.flink.ml.common.LabeledVectorimport org.apache.flink.ml.math.DenseVectorval survivalLV = survival.map{tuple =>val list = tuple.productIterator.toListval numList = list.map(_.asInstanceOf[String].toDouble)LabeledVector(numList(3), DenseVector(numList.take(3).toArray))}
然后我们可以使用这些数据来培训学习者。然而,我们将使用另一个数据集来例证构建学习者; 这将使我们能够展示如何导入其他数据集格式。
LibSVM文件
ML数据集的通用格式是LibSVM格式,可以在LibSVM数据集网站中找到使用该格式的许多数据集。FlinkML提供了readLibSVM通过MLUtils 对象提供的函数使用LibSVM格式加载数据集的实用程序。您还可以使用该writeLibSVM函数以LibSVM格式保存数据集。让我们导入svmguide1数据集。您可以在此处下载此处的 培训集 和测试集。这是一个astroparticle二元分类数据集,由Hsu等人使用。[3]在他们的实际支持向量机(SVM)指南中。它包含4个数字特征和类标签。
我们可以使用以下方法导入数据集:
import org.apache.flink.ml.MLUtilsval astroTrainLibSVM: DataSet[LabeledVector] = MLUtils.readLibSVM(env, "/path/to/svmguide1")val astroTestLibSVM: DataSet[LabeledVector] = MLUtils.readLibSVM(env, "/path/to/svmguide1.t")
这为我们提供了两个DataSet对象,我们将在下一节中使用它来创建分类器。
分类
导入训练和测试数据集后,需要为分类做好准备。由于SVMFlink仅支持的阈二进制值+1.0和-1.0,是因为它是使用标记的加载LIBSVM数据集之后需要转换1秒和0秒。
可以使用简单的规范化器映射函数完成转换:
def normalizer : LabeledVector => LabeledVector = {lv => LabeledVector(if (lv.label > 0.0) 1.0 else -1.0, lv.vector)}val astroTrain: DataSet[LabeledVector] = astroTrainLibSVM.map(normalizer)val astroTest: DataSet[(Vector, Double)] = astroTestLibSVM.map(normalizer).map(x => (x.vector, x.label))
一旦我们转换了数据集,我们就可以训练一个Predictor诸如线性SVM分类器。我们可以为分类器设置许多参数。这里我们设置Blocks参数,用于通过底层CoCoA算法[2]使用来分割输入。正则化参数确定 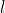 的量
的量 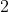 应用正则化,用于避免过度拟合。步长确定权重向量更新对下一个权重向量值的贡献。此参数设置初始步长。
应用正则化,用于避免过度拟合。步长确定权重向量更新对下一个权重向量值的贡献。此参数设置初始步长。
import org.apache.flink.ml.classification.SVMval svm = SVM().setBlocks(env.getParallelism).setIterations(100).setRegularization(0.001).setStepsize(0.1).setSeed(42)svm.fit(astroTrain)
我们现在可以对测试集进行预测,并使用该evaluate函数创建(真值,预测)对。
val evaluationPairs: DataSet[(Double, Double)] = svm.evaluate(astroTest)
接下来,我们将看到如何预处理数据,并使用FlinkML的ML管道函数。
数据预处理和管道
在使用SVM分类时经常鼓励的预处理步骤[3]是将输入要素缩放到[0,1]范围,以避免具有极值的特征支配其余部分。FlinkML具有许多Transformers诸如MinMaxScaler那些用于预处理的数据,和一个关键特征是能够链Transformers和Predictors在一起。这使我们能够运行相同的转换管道,并以直接和类型安全的方式对列车进行预测并测试数据。您可以在管道文档中阅读有关FlinkML管道系统的更多 信息。
让我们首先为数据集中的要素创建一个规范化转换器,并将其链接到一个新的SVM分类器。
import org.apache.flink.ml.preprocessing.MinMaxScalerval scaler = MinMaxScaler()val scaledSVM = scaler.chainPredictor(svm)
我们现在可以使用新创建的管道来对测试集进行预测。首先,我们再次调用fit,以训练缩放器和SVM分类器。然后,测试集的数据将被自动缩放,然后传递给SVM进行预测。
scaledSVM.fit(astroTrain)val evaluationPairsScaled: DataSet[(Double, Double)] = scaledSVM.evaluate(astroTest)
缩放的输入应该为我们提供更好的预测性能。
从这往哪儿走
本快速入门指南可以作为FlinkML基本概念的介绍,但您可以做更多的事情。我们建议您浏览FlinkML文档,然后尝试不同的算法。一个非常好的入门方法是使用来自UCI ML存储库和LibSVM数据集的有趣数据集。从像Kaggle或 DrivenData这样的网站处理一个有趣的问题也是通过与其他数据科学家竞争来学习的好方法。如果您想贡献一些新的算法,请查看我们的 贡献指南。
参考
[1]墨菲,凯文P. 机器学习:概率视角。麻省理工学院出版社,2012。
[2] Jaggi,Martin,et al。通信高效的分布式双坐标上升。神经信息处理系统的进展。2014年
[3]许志伟,张志忠和林志仁。 _支持矢量分类的实用指南。_2003。

