xgboost是机器学习目前使用最广、效率最高的工具。之前大概了解过xgboost的原理,说实话并没有真正的理解,甚至连它和Lightgbm的优势劣势在哪里都不知道。因此这次我打算来仔细研读陈天奇大神的Xgboost PPT,逐页翻译并加备注,这样也能帮助自己更好的理解这个算法。
原PPT链接:https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
一、监督学习的几点关键概念

xi属于实数空间,表示第i个训练集
模型:常见的即为线性模型,包括了线性回归和逻辑回归。线性回归是用来预测连续型y值的,如房价;逻辑回归是用来判断类别的,如是否离职。
参数w,即为我们需要通过数据来计算得到的值,学习的结果即为找到合适参数w,使得计算结果y ^ \hat{y}
y
^
接近最接近yi。

目标函数也是机器学习中最重要的函数,学习的目的是让目标函数打到最小值。常见的目标函数由两部分构成:损失函数,一般为预测值和实际值的差距,衡量的是模型有多适配训练集。另一部分为正则项,通常利用正则项来调节模式,避免过拟合。
对于损失函数,常见的有:
平方差,用于一般回归
逻辑差,也叫交叉熵损失(Cross Entropy Loss),常用于逻辑回归
对于正则项,常见的也有两种:
L2 模,即参数w的平方和再乘以系数λ
L1模,即参数w乘以系数λ
将以上几种分类合并起来,我们就能得到以下几种模型:
岭回归:线性回归模型+L2正则项,利用的是平方差损失函数
Lasso回归:线性回归模型+L1正则项,同样用平方差损失函数
逻辑回归:线性模型,交叉熵损失函数,L2正则项
将模型,参数,目标函数的概念分开讨论,在工程上也有益处,因为我们可以修改部分代码,就能部署不同的回归函数了。

这页继续强调了一下损失函数和正则项对于模型学习的不同作用。前者倾向于生成更具预测性的模型,避免欠拟合;而后者倾向于生成更简易的模型,避免过拟合。二者相辅相成。
二、 回归树集成
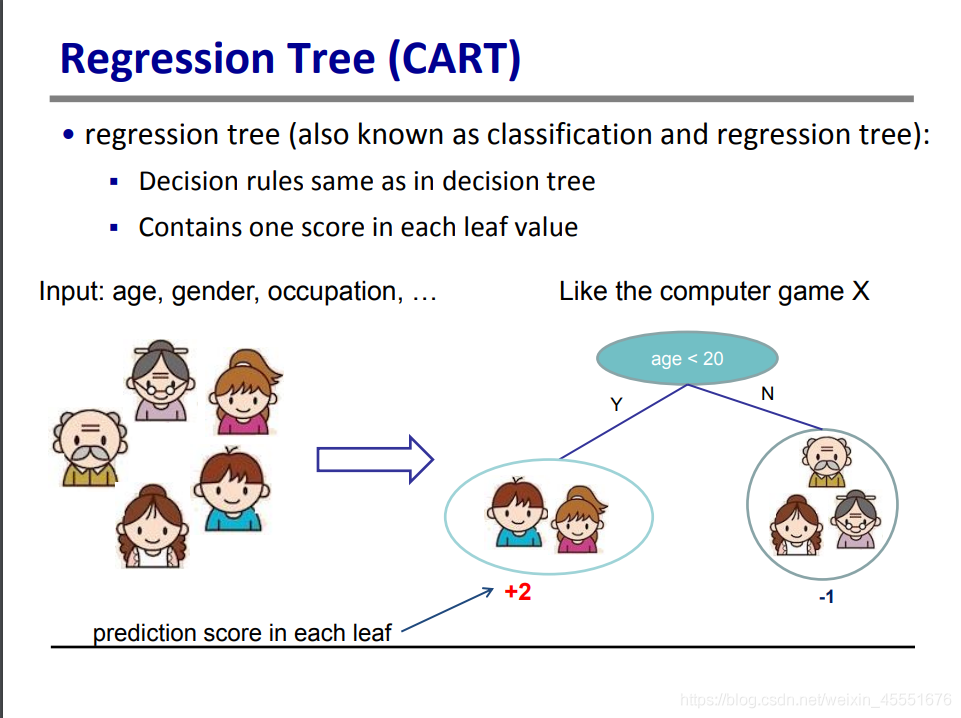
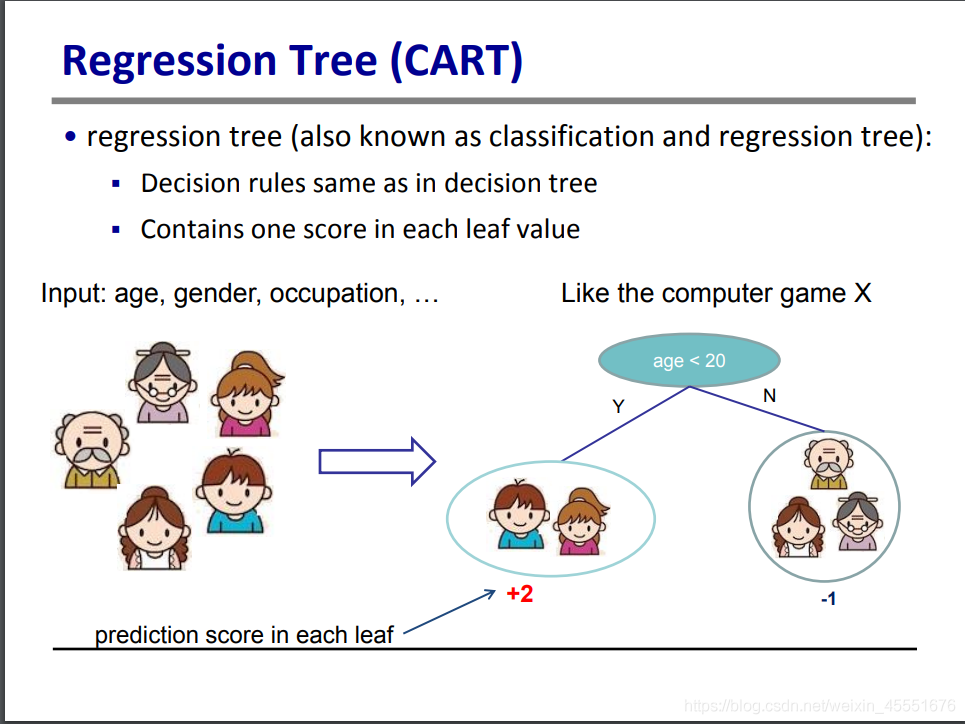
回归树模型是区别于线性模型的另一种模型,也叫CART(Classification And Regression Tree),特点是利用将特征分隔成不同的特征空间,每一个特征空间为一个叶子,每一片叶子有一个大粪。如图中所示,按照年龄分成了两组,两个叶子的得分分别为+2和-1分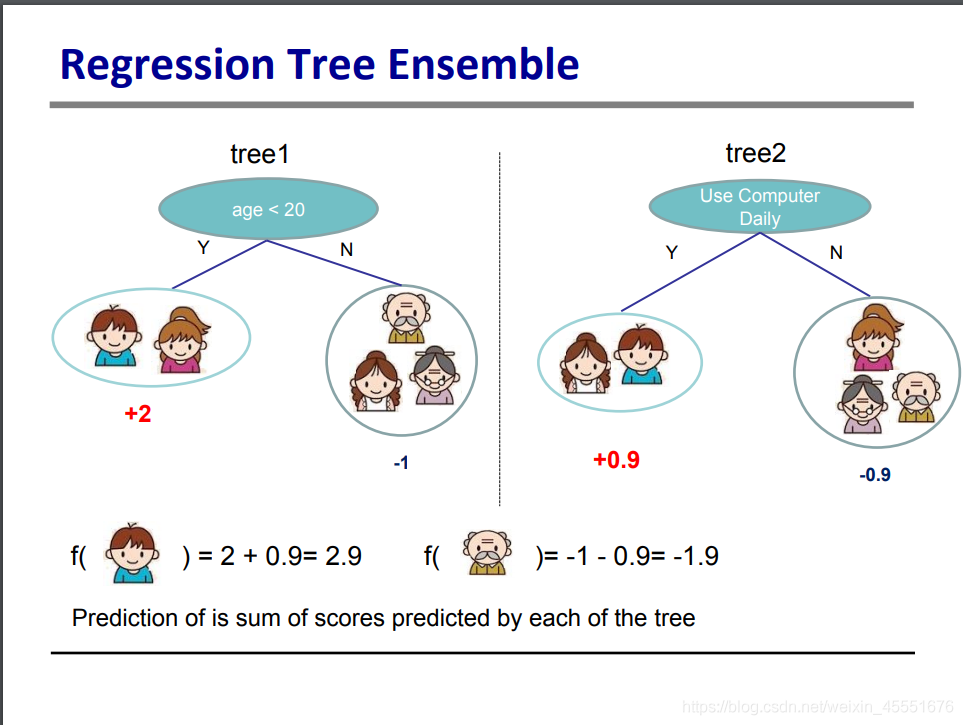
案例继续,现在有另一棵决策树,以是否用电脑为分界线,分割成两组,那么新的叶子又有两个得分0.9和-0.9。那么将两棵树合在一起看,就能得到具体某个元素(即xi)的得分,即为不同决策树所在叶子的得分之和。

树模型目前广泛适用于数据挖掘竞赛中,常见的有GBM(gradient boosting machine,一般叫做梯度提升树算法),和Random Forest(随机森林)
对输入不需要进行特征正则化
可以在不同变量中学习到高阶关系(如两个参数的乘积这类关系)
可规模化,并能使用于工业中。
现在开始详解树模型。
上文提到,可以将第i个数据,在不同的树中的得分累加起来,得到一个总得分,就是这页公式的含义。
y ^ \hat{y}
y
^
:样本在不同树模型中的总得分,也为模型预测值。
f k f{k}f
k
: 第k棵树的得分表,如在上文中,小于20岁得2分,大于20岁得0.9分,就是一种f函数。k棵树共有k种函数。
这里我们可以将f k f{k}f
k
视为一个参数来训练,好比线性模型中的w
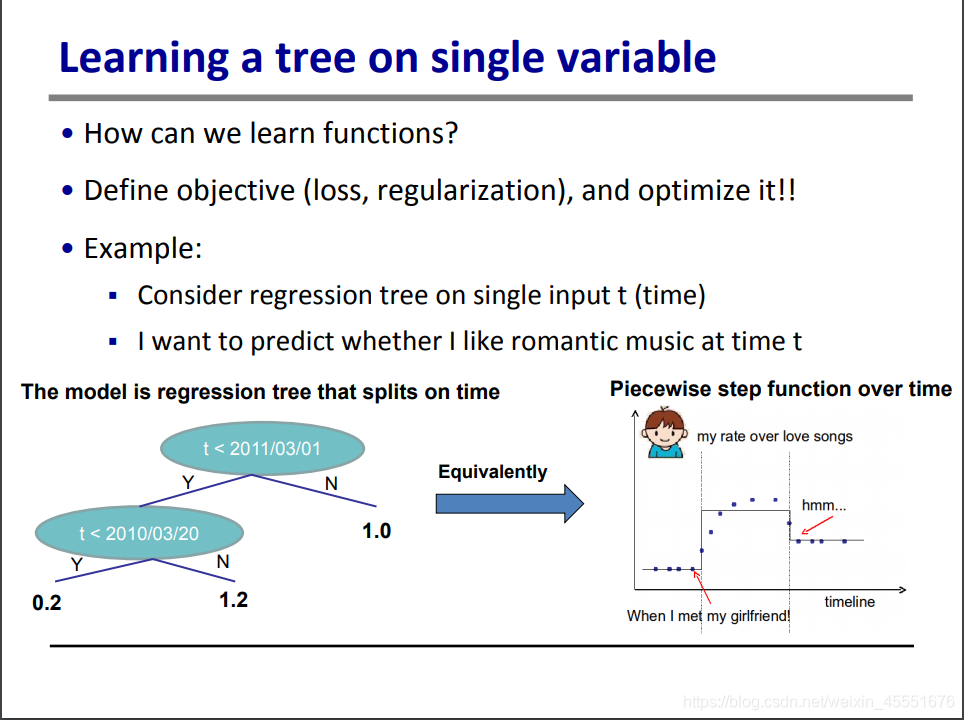
那我们应该如何学习这个参数(函数)呢?其实跟线性模型也是一样的,设置目标函数并通过训练优化它。
这里举了一个例子,如何预测我对浪漫音乐的喜爱程度(回归模型)。从散点图我们可以清晰的看到,可以将数据点分成三个阶段,即三个样本空间,可以最大程度拟合这个喜爱程度。
但是如果用到机器学习的手段,就需要一些优化过程了。
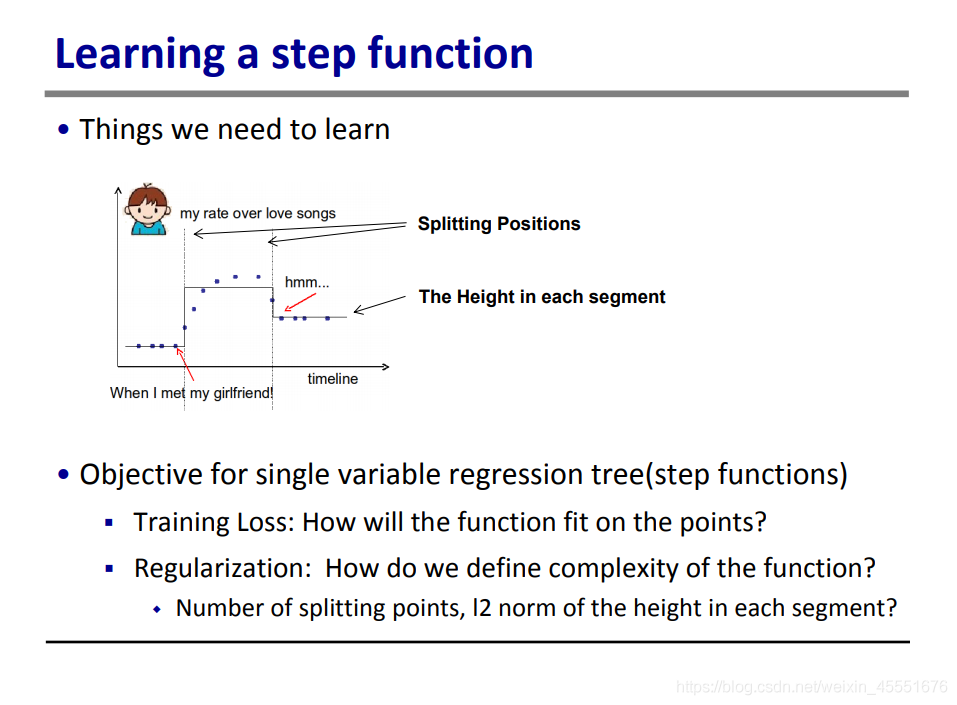
首先,需要确定的有两点,一个是需要多少个分裂点,这里可以理解为可以有多少棵树;其次,需要确定的是每一层的高度是多少,这里相当于是每一片叶子的得分。
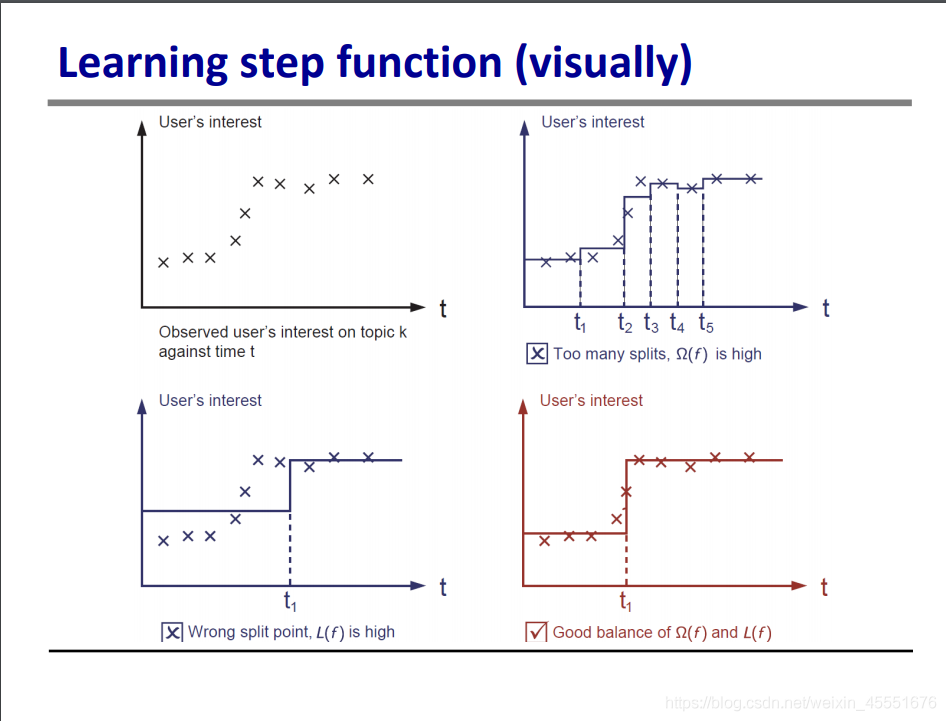
右上的图,分裂过多,虽然每一层的得分基本可以反应实际的结果,但是会造成过拟合。
左下的图,只有一棵分裂树,模型简易,但是由于分裂点位置错误,也导致了模型错误。
只有右下的图既保证了模型的准确性,又保证了简易型,防止过拟合。

根据以上案例,我们再回到模型建立的一般步骤中。
模型函数已知,现在来考虑目标函数。前文提到,目标函数分为了损失函数和正则项,这两项都与模型函数fk有关。
但是对于树模型,对正则项的定义也能简单一点,例如使用树的节点数、深度作为正则项,或者用叶深度的L2模作为正则项。
当我们在讨论决策树时,它通常是启发式的(heuristics):
根据信息增益分裂树。关于信息增益,简单来说是代表了在一个条件下,信息复杂度(不确定性)减少的程度。具体展开可以百度。
修剪树枝
设置最大深度
顺滑叶得分
启发式的学习方法其实和目标函数也是息息相关的,例如:
信息增益对应的是训练损失
剪枝对应了根据节点的正则化修正
最大深度对应了函数空间的最大限制
顺滑叶得分则对应了对叶权重的L2正则化。
既然是CART,顾名思义,它技能用于预测回归,也能用以预测分类,这与你的目标函数的选择相关。
例如,如果用平方差作为损失函数,那就能获得一个回归树,也就是常见的GBM(Gradient Boosting Machine)。
而如果选用交叉熵作为损失函数,就能得到LogitBoost。
三、梯度提升(Gradient Boosting)算法详解
再次强调了机器学习的几点特性:
偏差-方差平衡
损失函数+正则项所构成的目标函数应用于回归树训练
我们想要的是具有预测性和建议的函数

第一行为目标函数,其中l ( y i , y i ^ ) l(y{i},\hat{y{i}})l(y
i
,
y
i
^
)表示损失函数,第一项需要将对所有样本求和。Ω ( f k ) \Omega (f_{k})Ω(f
k
)表示正则项,需要对k个特征的正则项进行求和。
为了降低目标函数,既需要让损失函数降低,即拉近预测值与实际值之间的距离,又需要让正则项降低,即降低各个特征函数的权重。
在这里,我们没办法使用SGD(Stochastic Gradient Decent,随机梯度下降法)。因为SGD常用来寻找的是数值解,需要有已定的目标函数;但是在这里,我们需要在确定是一个函数,而非数值解,因此无法使用。
解决方案是使用加法模型提升。具体来说,是将每一次的预测值,转换为前一次的预测值加上一个函数f t ( x i ) f{t}(x{i})f
t
(x
i
)。注意这里的f t ( x i ) f{t}(x{i})f
t
(x
i
)和上文的Ω ( f k ) \Omega (f{k})Ω(f
k
)中的f k f{k}f
k
不是同一个函数。
这里对GBDT在做多一些解释,方便下文的理解。
GBDT的思想是累加多个弱学习器,以达到强学习器的效果。
每一棵树,就是一个弱分类器。例如大于10岁和小于10岁是一个弱分类器,性别是另一个弱分类器,把二者的得分相加起来,就能得到一个预测值y。
加法模型是GBDT的常见模型,他的思路是先训练一棵树,即弱分类器,计算弱分类器与实际值的差值。接着,将该差值传到下一个弱分类器中,再计算差值与下一个分类器的差值,以此迭代。如果换个方向讲,就是每一次迭代,预测值都等于了前一次的预测值,加上了这次的树。
对于加法模型,正则项也与SGD算法中的L1范式L2范式有区别。在GBDT中,常见的正则项处理方式有三种(摘自百度):
1. 第一种,是对步长的调节,即每一轮迭代中对新增的树乘上一个系数v,v属于[0,1]。对于同样的训练集学习效果,较小的步长意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
2. 第二种正则化的方式是通过子采样比例(subsample)。取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。
3. 第三种利用了决策树的剪枝,即正则项为α*T,T为叶子树,显然T无法过大,否则目标函数会过高。
那么我们要如何确定这个加法项ft呢,其实也是利用训练优化它。
这里先明确几个概念:
y ^ i ( t ) \hat{y}{i}^{(t)}
y
^
i
(t)
表示,第t次迭代的第i个变量所对应的预测值。
将所有变量的预测值求和,才是目标函数的第一项。
将加法公式y ^ i ( t ) = y ^ i ( t − 1 ) + f t ( x i ) \hat{y}{i}^{(t)}=\hat{y}{i}^{(t-1)}+f{t}(x{i})
y
^
i
(t)
=
y
^
i
(t−1)
+f
t
(x
i
)代入到目标函数中,可以将目标函数的第一项——损失函数变为:
∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) \sum{i=1}^{n}l(y{i},\hat{y}{i}^{(t-1)}+f{t}(x{i}))∑
i=1
n
l(y
i
,
y
^
i
(t−1)
+f
t
(x
i
))
其次,对于正则项,在原公式中,是对每一次迭代的残差函数f i f{i}f
i
求和。但是假如我们使用了上一页中提到的步长控制法,这一项其实仅与本次迭代有关。因此作者这里就将求和符号去掉了,仅留下了本次迭代所增加的决策树f t f{t}f
t
。
接着,作者举了一个例子,当损失函数为平方差时,即:
l ( y i , y ^ i ( t ) ) = ( y i − y ^ i ( t ) ) 2 = ( y i − y ^ i ( t − 1 ) − f t ( x i ) ) 2 l(y{i},\hat{y}{i}^{(t)})=(y{i}-\hat{y}{i}^{(t)})^2=(y{i}-\hat{y}{i}^{(t-1)}-f{t}(x{i}))^2l(y
i
,
y
^
i
(t)
)=(y
i
−
y
^
i
(t)
)
2
=(y
i
−
y
^
i
(t−1)
−f
t
(x
i
))
2
l ( y i , y ^ i ( t ) ) = ( y i − y ^ i ( t − 1 ) ) 2 − 2 ( y i − y ^ i ( t − 1 ) ) f t ( x i ) + f t ( x i ) 2 l(y{i},\hat{y}{i}^{(t)})=(y{i}-\hat{y}{i}^{(t-1)})^2-2(y{i}-\hat{y}{i}^{(t-1)})f{t}(x{i})+f{t}(x{i})^2l(y
i
,
y
^
i
(t)
)=(y
i
−
y
^
i
(t−1)
)
2
−2(y
i
−
y
^
i
(t−1)
)f
t
(x
i
)+f
t
(x
i
)
2
在这里,由于y i y{i}y
i
和y i ( t − 1 ) y{i}^{(t-1)}y
i
(t−1)
都是在上一轮算出来的,并且在这个公式中,仅有f t f{t}f
t
是变量,所以我们将第一项视为一个常数项,搬到最后,则原公式就变成了:
l ( y i , y ^ i ( t ) ) = 2 ( y ^ i ( t − 1 ) − y i ) f t ( x i ) + f t ( x i ) 2 l(y{i},\hat{y}{i}^{(t)})=2(\hat{y}{i}^{(t-1)}-y{i})f{t}(x{i})+f{t}(x{i})^2l(y
i
,
y
^
i
(t)
)=2(
y
^
i
(t−1)
−y
i
)f
t
(x
i
)+f
t
(x
i
)
2
而y i − y i ( t − 1 ) y{i}-y_{i}^{(t-1)}y
i
−y
i
(t−1)
也可以视为上一轮的残差。

在上一页的PPT中,我们将平方差的损失函数进行了简化。而在这一页中,我们需要证明,对任意的损失函数,我们都能有类似的简化。
主要用到的方法,就是泰勒展开。
对于损失函数l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) l(y{i},\hat{y}{i}^{(t-1)}+f{t}(x{i}))l(y
i
,
y
^
i
(t−1)
+f
t
(x
i
)),我们将( y i , y ^ i ( t − 1 ) ) (y{i},\hat{y}{i}^{(t-1)})(y
i
,
y
^
i
(t−1)
)视为x,将f t ( x i ) f{t}(x{i})f
t
(x
i
)视为Δ x \Delta xΔx,那么f ( x ) f(x)f(x)就为l ( y i , y ^ i ( t − 1 ) ) l(y{i},\hat{y}{i}^{(t-1)})l(y
i
,
y
^
i
(t−1)
)。
在这里,y i y{i}y
i
也是一个常数。因此自变量x中,实际只有一个y ^ i ( t − 1 ) \hat{y}{i}^{(t-1)}
y
^
i
(t−1)
。那么我们对x求导数,就能得到一个偏微分:
∂ ( l ( y i , y ^ ( t − 1 ) ) ) ∂ ( y ^ ( t − 1 ) ) \frac{\partial (l(y{i},\hat{y}{(t-1)}))}{\partial (\hat{y}{(t-1)})}
∂(
y
^
(t−1)
)
∂(l(y
i
,
y
^
(t−1)
))
或者简化为:∂ ∂ y ^ ( t − 1 ) l ( y i , y ^ ( t − 1 ) ) ) \frac{\partial }{\partial \hat{y}{(t-1)}} l(y{i},\hat{y}{(t-1)}))
∂
y
^
(t−1)
∂
l(y
i
,
y
^
(t−1)
)),即为PPT中的g i g{i}g
i
同理,二次求导之后也能得到h i h{i}h
i
。
在这里,尽管gi和hi都是用偏导数表示,但是只要已知损失函数,一阶导数和二阶导数都能很容易求得。
如果仍然以平方差损失函数为例,我们可以很容易求得一阶导数和二阶导数,恰好就是我们在上一页PPT中计算出来的结果。
经过一系列的努力,我们将目标函数简化到了三个变量上:g i g{i}g
i
, h i h{i}h
i
,f t f_{t}f
t
。其中,前两项都能轻易计算得出,并且不随着树的变化而变化。
这在工程上对我们的帮助也极大。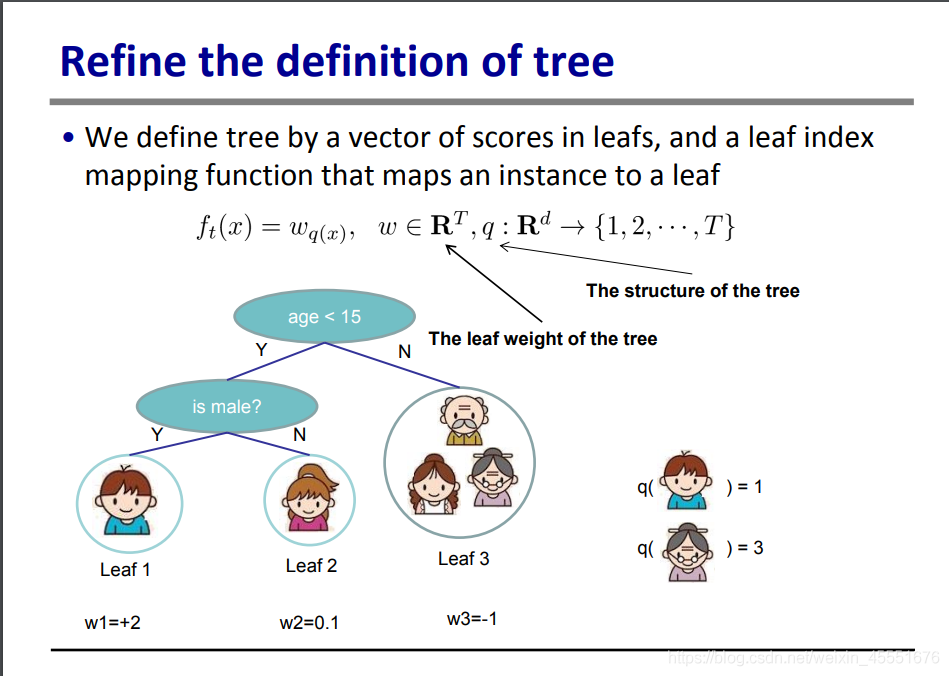
现在我们来对树的定义做一些调整。
我们定义了两个变量,叶分数,和叶指数。所谓叶分数,就是该叶子,或者该群组的得分;而叶指数,就是对叶子的排序,如图中的leaf1, leaf2,1和2就是叶指数。
这里还定义了上文中的函数f t ( x ) = w q ( x ) f{t}(x)=w{q(x)}f
t
(x)=w
q(x)
。在这里,q(x)表示第x个元素的叶指数,也就是第x个元素所在的叶子的位置。如q(男孩)=1,表示男孩是在第一个叶子中,q(奶奶)=3,表示奶奶在第三个叶子中。由于指数一定是正整数,所以q一定是在正整数集中。
而w,就是叶分数,即这个叶子对应的得分。如第一个叶子的得分是+2,则w1=+2。由于这个评分可正可负,因此属于实数集。
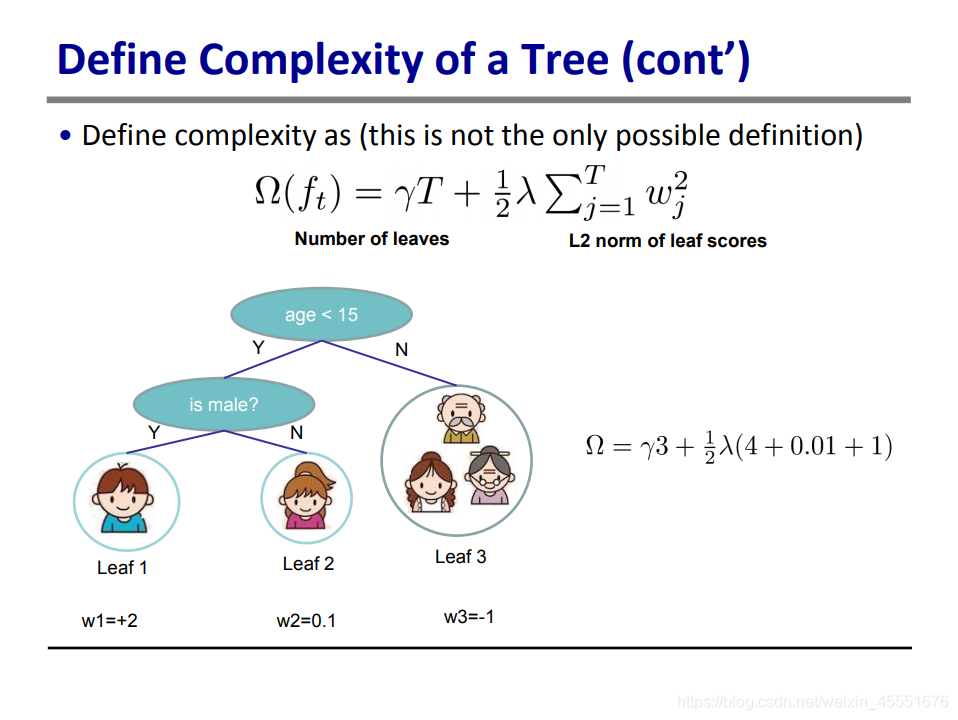
定义完了f t f{t}f
t
,我们再来定义Ω ( f t ) \Omega(f{t})Ω(f
t
)。
上文提到,在加法模型中,正则项主要有三类:1. 步长调节,2. 采样比例,3. 剪枝。在这里,作者设计的正则项用到了第一种和第三种。
我们看第一项,γ T \gamma TγT,这项实际就是第三种正则法:剪枝。对叶子数量乘上一个系数,可以有效防止叶子过多。
再看第二项,w是上文中的f t f_{t}f
t
的值,也就是每一次迭代的增加值。那么对这个值的平方再乘上系数,实际上也是第一种正则法,步长调节。取平方求和的方法也类似SGD中的L2模,能够有效控制梯度增长的速度,以提高模型精度。
接着,作者把T=3,w1=+2, w2=0.1, w3=-0.1代入到原公式中,就可以得到Ω的值了,也就是本轮迭代的正则项(γ和λ都视为常数)。
好了,我们现在将正则项再代回原目标函数中,做合并同类项,可以把w也放到求和项中。
这里需要注意,在正则项中,是T个w 2 w^2w
2
累加,而再损失函数中,是n个自变量w 2 w^2w
2
累加。因此,我们需要将求和号Σ统一成T个累加。在前面的图中,我们可以知道,一个叶子中可能会有多个自变量。把一个叶子中所有自变量的gi和hi累加起来,就是公式里Σ i ∈ I j \Sigma{i \in I{j}}Σ
i∈I
j
的含义。
那么我们可以看到,经过不懈的努力我们将求和号中的公式,变成了关于w j w_{j}w
j
的一元二次方程。

在这一页,我们复习了一下高中里一元二次方程的最值求解。对于G x + 1 / 2 H x 2 Gx+1/2Hx^2Gx+1/2Hx
2
,当x = − G / H x=-G/Hx=−G/H时,该方程能取到最小值− 1 2 G 2 H -\frac {1} {2} \frac {G^2} {H}−
2
1
H
G
2
。
那只要我们把上文的一元二次方程做类似的处理,就能知道:
当每一个叶子中的w ww都能取到− G j H j + λ -\frac {G{j}} {H{j}+\lambda}−
H
j
+λ
G
j
时,目标函数能够取到最小值。
不过这里实际上有两个假设:
树的结构已经定下来了。即每一片叶子中分配了哪些元素,都已经定好了。
我们对每一片叶子取到损失函数最小值,以此达到整体的最小值。实际上,这个最小值有可能仅是局部最小值,不一定就是全局最小值。
这一页就是对上一页的公式进行数值展示,此处不再赘述。

这里再次总结了饿一下,我们已经把目标函数变成了仅与G, H, γ,λ和T这五项已知参数有关的函数,把之前的变量f t f_{t}f
t
消灭掉了,也就不需要对每一个叶子进行打分了!
那么现在问题来,刚才我们提到,以上这些是假设树结构确定的情况下得到的结果。但是树的结构有好多种,我们应该如何确定呢?
这里作者用的方法是贪婪法。
我们假设现在迭代到了第i次,此时一共有T个树叶。此时,我们要对其中一个叶子进行分裂,把里面的群组分成了左边部分和右边部分。那么分裂后,目标函数就变成了:
O b j 分 裂 后 = l 左 + l 右 + γ ( T + 1 ) Obj{分裂后}=l{左}+l{右}+\gamma (T+1)Obj
分裂后
=l
左
+l
右
+γ(T+1)
O b j 分 裂 后 = − 1 2 G 左 2 H 左 + λ − 1 2 G 右 2 H 右 + λ + γ ( T + 1 ) Obj{分裂后}=-\frac {1} {2} \frac {G{左}^2} {H{左}+\lambda}-\frac {1} {2} \frac {G{右}^2} {H{右}+\lambda}+\gamma (T+1)Obj
分裂后
=−
2
1
H
左
+λ
G
左
2
−
2
1
H
右
+λ
G
右
2
+γ(T+1)
假如没有分裂,那之前的应该是:
O b j 分 裂 前 = − 1 2 G 总 2 H 总 + λ + γ T Obj{分裂前}=-\frac {1} {2} \frac {G{总}^2} {H{总}+\lambda}+\gamma TObj
分裂前
=−
2
1
H
总
+λ
G
总
2
+γT
其中,G 总 = G 左 + G 右 G{总}=G{左}+G{右}G
总
=G
左
+G
右
, H 总 = H 左 + H 右 H{总}=H{左}+H{右}H
总
=H
左
+H
右
因此,将分裂前的目标函数,减去分裂后的目标函数,就能得到分裂带来的目标函数增益:
G a i n = 1 2 [ G 左 2 H 左 + λ + G 右 2 H 右 + λ − ( G 左 + G 右 ) 2 H 左 + H 右 + λ ] − γ Gain=\frac {1} {2}[\frac {G{左}^2} {H{左}+\lambda}+\frac {G{右}^2} {H{右}+\lambda}-\frac {(G{左}+G{右})^2} {H{左}+H_{右}+\lambda}]-\gammaGain=
2
1
[
H
左
+λ
G
左
2
+
H
右
+λ
G
右
2
−
H
左
+H
右
+λ
(G
左
+G
右
)
2
]−γ
增益越大,意味着分裂前比分裂后的差距越大,也就意味着梯度下降得越明显。
这里举了个例子,当xj
寻找分裂的算法:
对每一个节点,即已有的叶,遍历所有特征
对每一个特征,按特征所对应的叶值进行排序
用线性扫描,决定最佳分裂位置。
用最佳分裂生成新的节点(叶)
生成K深度树的时间复杂度:
对于每一层,需要O时间去做一次排序,并且要做K层。
后期可以继续优化
适用于非常大的数据集
有些算法会将数值型变量和排序型变量分开处理。
但是我们的算法是用打分来往下分裂的,所以同样适用于排序型变量。
实际上,我们还能用独热编码,将排序型变量转换为0-1数值变量,就可以直接进行分类处理。
这样操作可以形成稀疏矩阵,方便学习。
我们再回顾一下之前的公式,对于分裂增益,实际上是有可能为负值的,即当损失函数的增益小于正则项参数γ时,增益即为负。
当遇到这种情况时,我们就要停止继续分裂,这种叫做“提前停止”
不过实际上,一个负增益的分裂有可能是会在未来产生一个更佳的分裂
或者,我们也可以先将树生长到最佳深度,再将所有负增益的叶子剪掉,这叫“后剪枝”。

我们最后整理一下整个算法逻辑:
在每一次迭代中新增一棵树。
在迭代开始前,先计算两个参数:g i g{i}g
i
和h i h{i}h
i
,这两个参数仅与上一轮所得的y ^ \hat{y}
y
^
,这一轮的yi,以及损失函数的设置有关。
利用遍历法找到最佳分裂点,生成一个新的树。此时f t ( x ) = − G H + λ f{t}(x)=-\frac {G} {H+\lambda}f
t
(x)=−
H+λ
G
把f t ( x ) f{t}(x)f
t
(x)加到加法模型中,就可以获得这轮迭代的y ^ \hat{y}
y
^
。
不过通常我们会在f t ( x ) f_{t}(x)f
t
(x)前再加上一个参数ϵ \epsilonϵ,用来调整步长,通常设置为0.1.
这样的话,我们每一步就不是充分优化,这样可以防止过拟合。
四、总结
提出了两个问题:
我们如果用上述分类器是解决权重回归问题。
对于时间序列,我们是否有其他方法去学习时间分裂的方法?
对于第一个问题,就是在损失函数(平方差公式)前面加上一个参数a,就可以解决问题了。
对于时间序列问题,除了自上而下的贪婪法之外,还能用自下而上的贪婪法,即从独立点出发,考虑合并其他独立点,是否可以使梯度增加。

最后总结,XGBoost其实是巧妙设置了损失函数和正则项,使得计算过程得到了充分的简化,效率大大提高。
之后我会再看一下lightGBM, RF等其他算法,再写一份对比的文章出来。
不,是你的杰宝
关注
9

