题目链接
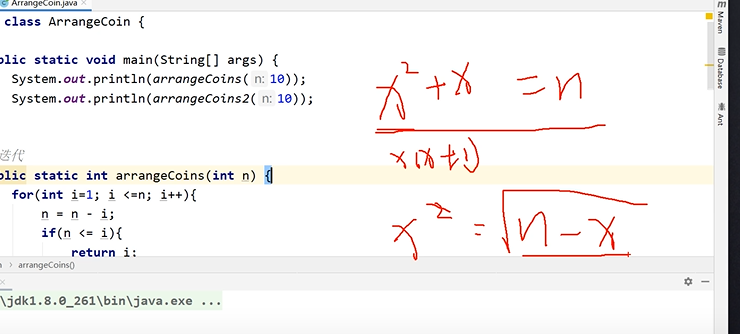
    image.png
    牛顿迭代公式：
    image.pngimage.png

    1. class Solution {
    2.     public int arrangeCoins(int n) {
    3.         // return arrangeCoins1(n);
    4.         return arrangeCoins2(n);
    5.         // return arrangeCoins3(n);
    6.     }
    8.     // 1.迭代
    9.     public int arrangeCoins1(int n) {
    10.         int num = 1;
    11.         while(num <= n) {
    12.             n = n - num;
    13.             num ++;
    14.         }
    15.         if(num == n) return n;
    16.         return num-1;
    17.     }
    19.     // 2.二分查找（因为不满足的行数一定是小于n的，所以。。）, 前x项和为：(1+x)*(x/2)
    20.     public int arrangeCoins2(int n) {  // int类型的范围
    21.         int left = 1,right = n;
    22.         while(left <= right) {
    23.             int mid = (right - left)/2 + left;
    24.             long num = (long)(mid+1)*mid;
    25.             if(num == (long)2*n) {
    26.                 return mid; 
    27.             } else if(num > (long)2*n) {
    28.                 right = mid - 1;
    29.             } else {
    30.                 left = mid + 1;
    31.             }
    32.         }
    33.         return left-1;
    34.     }
    36.     // 3.牛顿迭代, 1804289383过不去，会发生栈溢出
    37.     public int arrangeCoins3(int n) {
    38.        if(n == 0) return 0;
    39.        return (int)sqrt(n,n);
    40.     }
    42.     private double sqrt(double x, int n) {
    43.         double res = (x + (2*n - x)/x)/2;
    44.         if(res == x) {
    45.             return res;
    46.         } else {
    47.             return sqrt(res,n);
    48.         }
    49.     }
    50. }