1649. Create Sorted Array through Instructions[树状数组]

https://leetcode.com/problems/create-sorted-array-through-instructions/
树状数组的典型问题，学习一下

个人解答

class Solution:
    def createSortedArray(self, nums: List[int]) -> int:
        N = max(nums) + 1
        c = [0] * N
        def getSum(c, x):
            res = 0
            while x > 0:
                res += c[x]
                x -= x & -x
            return res
        def update(c, x):
            while x < len(c):
                c[x] += 1
                x += x & -x
        res = 0
        for i, x in enumerate(nums):
            res += min(getSum(c, x - 1), i - getSum(c, x))
            update(c, x)
        return res % (10**9+7)

题目分析

本题比较容易看出，是一个考察数据结构的题目，整个题目是以很直白的方式说明，没有各种算法的选择，单纯是数据结构的设计。

通过题目描述可以看出，需要对数组进行两个操作：

• 添加元素
• 计算元素左右区间的某一属性（小于/大于的元素个数）

涉及到动态的区间查询，基本上要用到类似于线段树这样的数据结构，但本题也没有那么的直白。线段树本来支持的操作是，修改与查询，但这里是添加元素，同时还要计算小于/大于的元素个数，因此要对问题做一个转化，将添加元素转化为修改元素，并能够维护大小关系！

用数组存储 [1, max(nums)] 区间的元素个数，初始都是0
如此一来：

• 添加一个数，只是对应数字的值+1
• 计算小于数字数量，即计算该数字之前的前缀和
• 计算大于数字数量，即计算该数字之后的和，也就是总数-当前数字对应的前缀和

这就是一个标准的单点修改，区间查询的操作了

可以通过线段树解决：

最直观的，递归方式的线段树：（有概率超时）

class Solution:
    def createSortedArray(self, nums: List[int]) -> int:
        N = max(nums) + 1
        depth = int(math.ceil(math.log2(N)))
        tree = [0] * (2 * 2 ** depth - 1)
        def update(tree, curr, l, r, x):
            tree[curr] += 1
            if l == r:
                return
            mid = (l + r) // 2
            if x <= mid:
                update(tree, 2 * curr + 1, l, mid, x)
            else:
                update(tree, 2 * curr + 2, mid + 1, r, x)
        def getPreSum(tree, curr, l, r, x): # inclusive
            if x >= r:
                return tree[curr]
            if x < l:
                return 0
            mid = (l + r) // 2
            return getPreSum(tree, 2 * curr + 1, l, mid, x) + getPreSum(tree, 2 * curr + 2, mid + 1, r, x)
        res = 0
        for i, x in enumerate(nums):
            res += min(getPreSum(tree, 0, 0, N - 1, x - 1), i - getPreSum(tree, 0, 0, N - 1, x))
            update(tree, 0, 0, N - 1, x)
        return res % (10 ** 9 + 7)

优化后线段树 迭代（勉强通过）

class Solution:
    def createSortedArray(self, nums: List[int]) -> int:
        N = max(nums) + 1
        tree = [0] * (2 * N)
        def update(tree, x):
            i = N + x
            tree[i] += 1
            while i > 1:
                tree[i >> 1] = tree[i] + tree[i ^ 1]
                i >>= 1
        def getPreSum(tree, x): # inclusive
            # sum: [0, x]
            l = N
            r = N + x
            res = 0
            while l <= r:
                if l & 1 == 1:
                    res += tree[l]
                    l += 1
                l >>= 1
                if r & 1 == 0:
                    res += tree[r]
                    r -= 1
                r >>= 1
            return res
        res = 0
        for i, x in enumerate(nums):
            res += min(getPreSum(tree, x - 1), i - getPreSum(tree, x))
            update(tree, x)
        return res % (10 ** 9 + 7)

树状数组

本题的特征，更推荐使用树状数组，简洁高效
树状数组算是线段树的一个子集，通过一定程度的简化，对于一些简单问题，可以用更简洁更高效的操作代替树状数组复杂的操作，本题满足这样的条件。

树状数组实现特别简洁，但是搞明白并不是很容易，一个比较入门的解释：https://www.bilibili.com/video/BV1pE41197Qj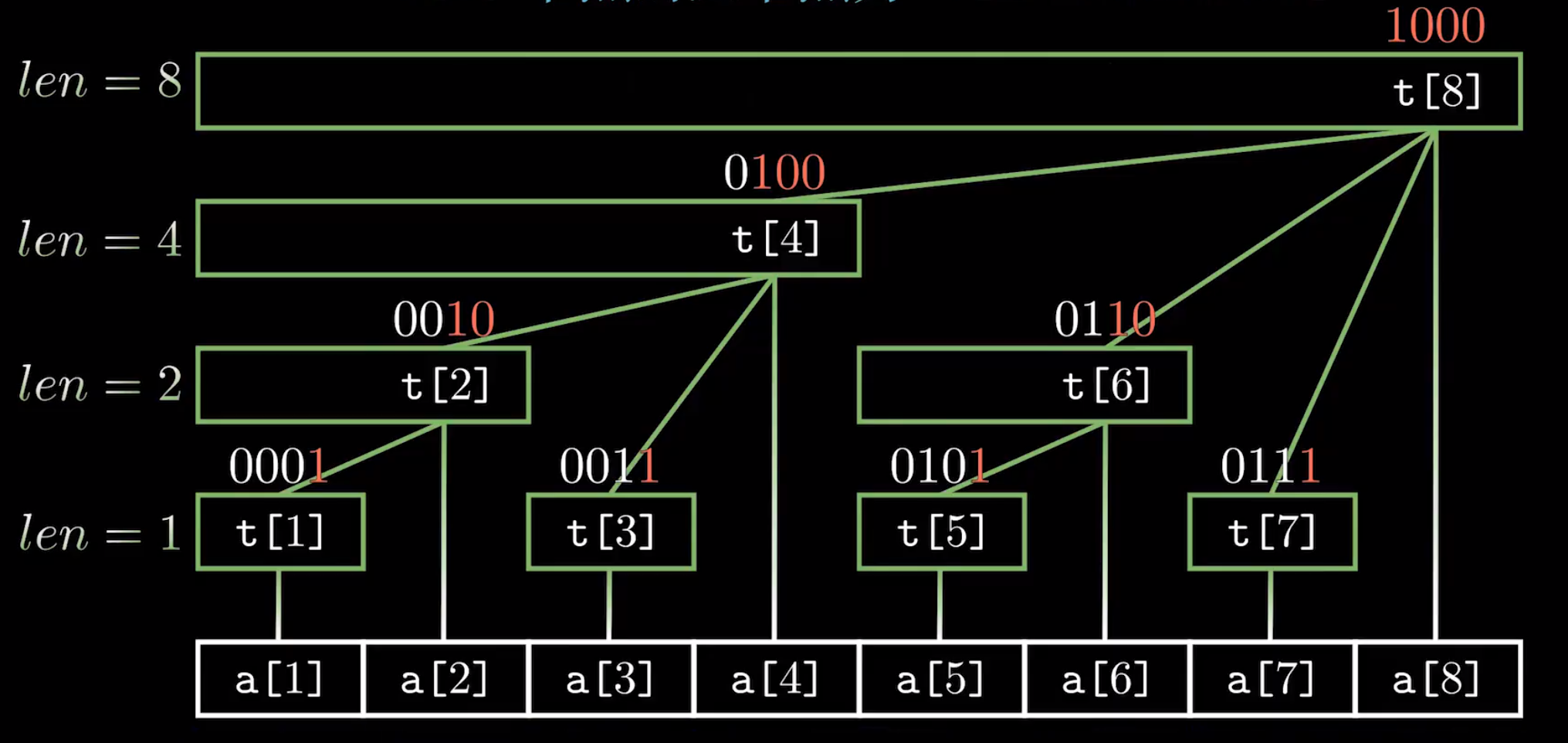

树状数组大致长上图这个样子，先不管为什么要这样设计，先了解具体有什么样的特征（然后发现，发明这玩意的人真他娘是个天才）

原始数组为 a ，8个元素（下标从1开始）
树状数组为 t ，同样8个元素，不过存储了原始数组的一些区间信息（区间和）
例如， t[8] 存储了1~8的区间和， t[6] 存储了5~6的区间和
为什么用这样的结构呢，我们来看一看这样的树结构的性质，尤其关注下标的二进制表示

在这之前，需要先有一个操作： lowbit(x) ，这个操作可以得到一个数二进制表示只保留最后一位之后得到的结果，例如：

• lowbit(0b10010) = 0b10
• lowbit(0b1001) = 0b1

这个操作可以通过： lowbit(x) = x & ~x 来得到，为什么可以，用补码表示简单推导一下就能得到

为什么引入这么一个操作呢，因为有了它，树状数组的操作变得异常简洁：

• 当前节点x的父节点： x + lowbit(x)
• 当前节点x的前一个子树： x - lowbit(x)

amazing!!!!

那么我们来看下单点修改的操作：从对应位置一路向上更新父节点就好，一路+lowbit(x)
那么前缀和查询呢：对应位置一路往前加，一路-lowbit(x)

这下明白为啥这样设计了吧，能做到两个操作极其简洁高效的处理，牛逼！！！！！

那么回到这道题，如果用树状数组的话，也是比较清晰的：

• 初始都为0
• 每次计算当前数之前的前缀和 以及 包含当前数的前缀和（用总数减去，就得到了比当前数大的）
• 在这之后插入该数（更新对应值+1）

解法见个人解答，参考：https://leetcode.com/problems/create-sorted-array-through-instructions/discuss/927531/JavaC%2B%2BPython-Binary-Indexed-Tree