https://leetcode.com/problems/range-sum-query-mutable/
可以说是线段树最经典的题目了！值得记住！

个人解答

  1. class NumArray:
  3.     def __init__(self, nums: List[int]):
  4.         if not nums:
  5.             return
  6.         self.N = len(nums)
  7.         self.D = int(math.ceil(math.log2(self.N))) # depth of segment tree
  8.         # use binary heap liked array to store segment tree, max size: 2^(1 + d) - 1
  9.         self.segmentTree = [0] * (2 * 2 ** self.D - 1)
  11.         # recursive construct tree
  12.         def construct(tree, i, l, r):
  13.             if l == r:
  14.                 tree[i] = nums[l]
  15.                 return tree[i]
  17.             mid = (l + r) // 2
  18.             tree[i] = construct(tree, i * 2 + 1, l, mid) + construct(tree, i * 2 + 2, mid + 1, r)
  19.             return tree[i]
  21.         construct(self.segmentTree, 0, 0, self.N - 1) # [l, r], inclusive
  23.     # recursive update
  24.     def _update(self, p, l, r, i, val):
  25.         if l == r:
  26.             diff = val - self.segmentTree[p]
  27.             self.segmentTree[p] += diff
  28.             return diff
  30.         mid = (l + r) // 2
  31.         if i <= mid:
  32.             diff = self._update(2 * p + 1, l, mid, i, val)
  33.         else:
  34.             diff = self._update(2 * p + 2, mid + 1, r, i, val)
  36.         self.segmentTree[p] += diff
  37.         return diff
  39.     def update(self, i: int, val: int) -> None:
  40.         self._update(0, 0, self.N - 1, i, val)
  42.     # recursive get sum
  43.     def _sum(self, p, l, r, i, j):
  44.         if i <= l and j >= r:
  45.             return self.segmentTree[p]
  46.         if i > r or j < l:
  47.             return 0
  49.         mid = (l + r) // 2
  50.         return self._sum(2 * p + 1, l, mid, i, j) + self._sum(2 * p + 2, mid + 1, r, i, j)
  52.     def sumRange(self, i: int, j: int) -> int:
  53.         return self._sum(0, 0, self.N - 1, i, j)
  58. # Your NumArray object will be instantiated and called as such:
  59. # obj = NumArray(nums)
  60. # obj.update(i,val)
  61. # param_2 = obj.sumRange(i,j)

题目分析

看线段树之前，先简单分析题目。
sum的操作很容一想到prefixSum这样的方式，在immutable的前置题目里也是用这样的方式，但是加了第二个操作：update之后，就不能了。

  1. 如果用prefixSum，那么getSum为O(1)，但是update是O(n)
  2. 如果不用，getSum为O(n)，update为O(1)

而题目中表示两个操作的数量差不多，因此两者都可能超时。
需要找到两个操作都是O(logn)的方法，也就要用到线段树。

线段树

https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/
https://oi-wiki.org/ds/seg/

已经讲的很清楚了，简易说明一下。

线段树首先是一个二叉树，不过它具有一些性质以用来维护区间的信息，可以支持O(logn)时间内的修改元素，区间查询（求和，最大值，最小值等）

线段树中存储的值：

  1. 叶节点存储元素的值
  2. 非叶节点存储区间信息

线段树父子节点关系：

  1. 父节点表示的区间是两子节点区间的拼接
  2. 父节点存储的值，是子节点值的合并

线段树可以用数组表示，类似于二叉堆：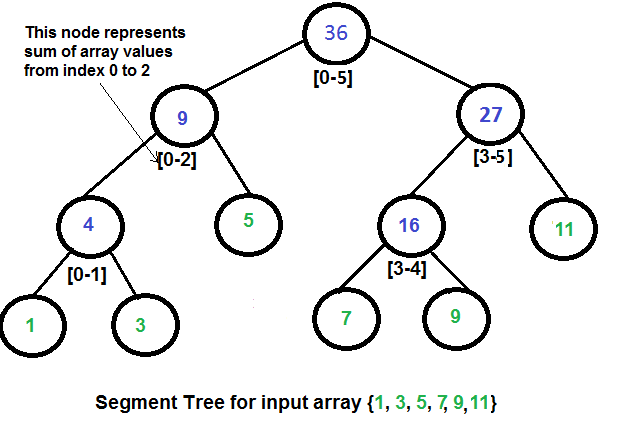
307. Range Sum Query - Mutable 线段树 - 图1
可表示为： {36, 9, 27, 4, 5, 16, 11, 1, 3, DUMMY, DUMMY, 7, 9, DUMMY, DUMMY}
这样一来，就可以

  • 用数组的下标表示父子区间关系：下标 i 对应的子节点在 2 * i + 1 和 2 * i + 2 中
  • 用数组中的值表示元素的值/区间的值

这样的线段树的构建/修改/查询的策略非常类似，均是递归进行即可，修改和查询的单个操作的复杂度都是Olog(n)

具体在实现过程中，有需要注意的一个小地方：
在选择范围的时候，可以考虑用 [l, r] ，也就是闭区间，如初始的时候为 [0, len - 1] ，这样更便于操作，算是具体实现时的一个比较小的tip
其余实现参照代码即可，整体逻辑还是很清晰的。

其它解法

这个题目有用binary index tree做的，但是自己对这个结构与线段树一样，同样不了解，暂且不谈。
除此之外，有用语言相关的一些内置快速修改或者求和的方法做的，这个已经超出了算法的范畴。
具体可以看：
https://leetcode.com/problems/range-sum-query-mutable/discuss/75741/Segment-Tree-Binary-Indexed-Tree-and-the-simple-way-using-buffer-to-accelerate-in-C%2B%2B-all-quite-efficient
https://leetcode.com/problems/range-sum-query-mutable/discuss/75802/%220-lines%22-Python

另外，线段树可以不用递归，而用一些数组的操作代替，而且加上位运算之后，特别简洁，令人惊叹：

  1. class NumArray(object):
  3.     def __init__(self, nums):
  4.         self.l = len(nums)
  5.         self.tree = [0]*self.l + nums
  6.         for i in range(self.l - 1, 0, -1):
  7.             self.tree[i] = self.tree[i<<1] + self.tree[i<<1|1]
  9.     def update(self, i, val):
  10.         n = self.l + i
  11.         self.tree[n] = val
  12.         while n > 1:
  13.             self.tree[n>>1] = self.tree[n] + self.tree[n^1]
  14.             n >>= 1
  17.     def sumRange(self, i, j):
  18.         m = self.l + i
  19.         n = self.l + j
  20.         res = 0
  21.         while m <= n:
  22.             if m & 1:
  23.                 res += self.tree[m]
  24.                 m += 1
  25.             m >>= 1
  26.             if n & 1 ==0:
  27.                 res += self.tree[n]
  28.                 n -= 1
  29.             n >>= 1
  30.         return res

参考：https://leetcode.com/problems/range-sum-query-mutable/discuss/75802/“0-lines”-Python/221484