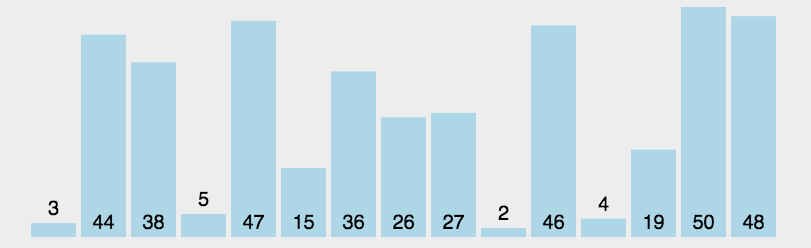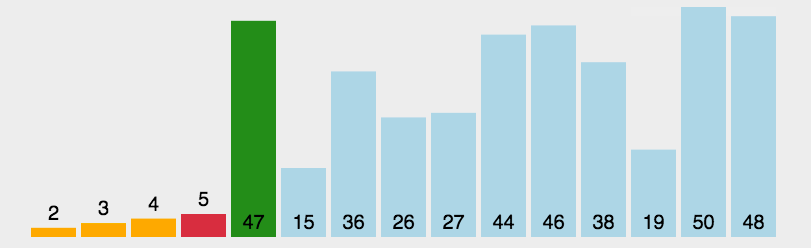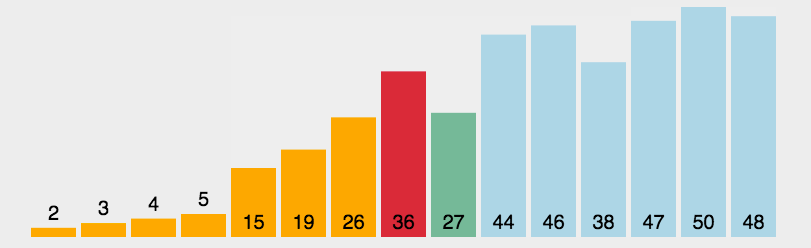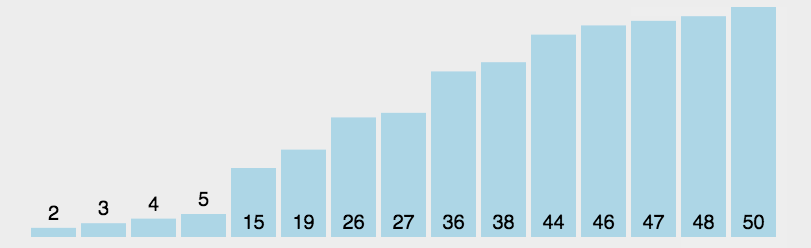
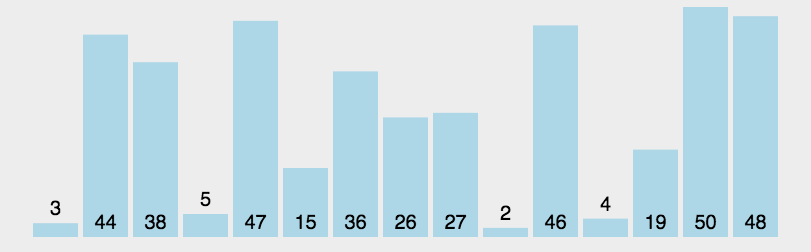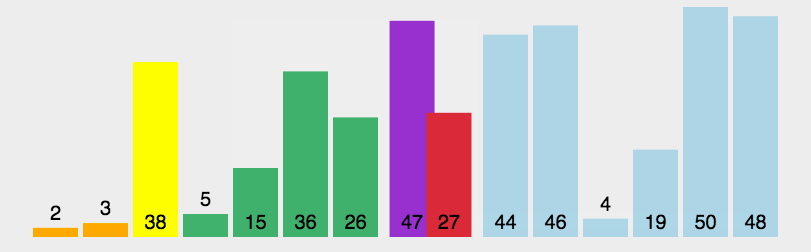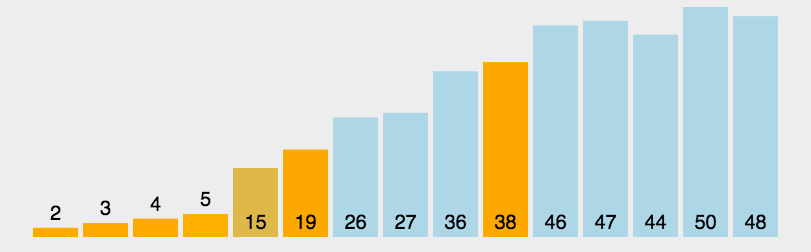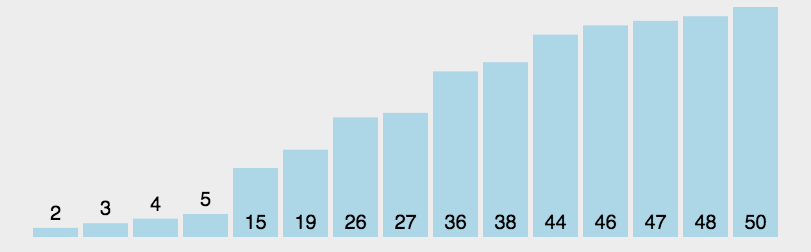
冒泡排序
- 时间复杂度
- 最佳情况:T(n) = O(n)
- 最差情况:T(n) = O(n2)
- 平均情况:T(n) = O(n2)
- 算法描述:
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
- 动图演示:
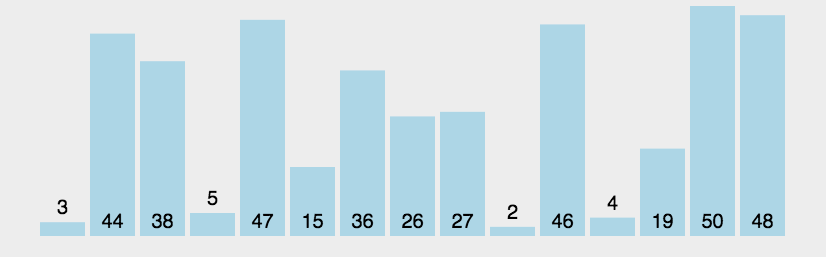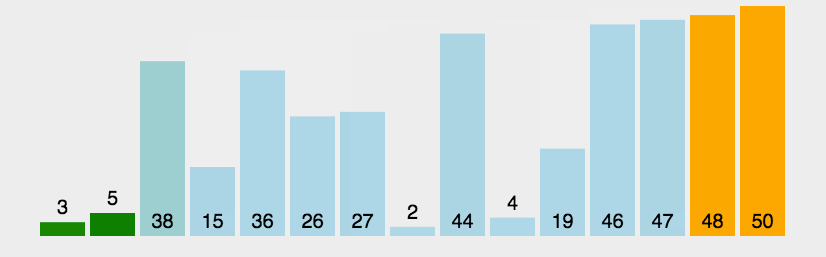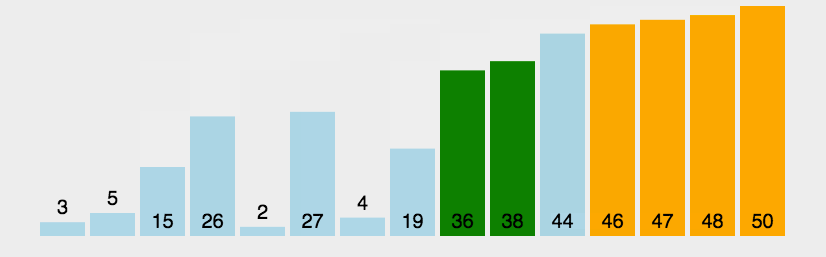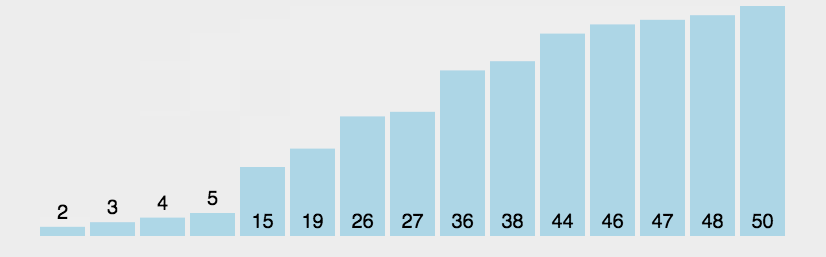
代码实现: |
6. /*
6. Description:冒泡排序
6.
6. @param array 需要排序的数组
6. @author JourWon
6. @date 2019/7/11 9:54
6. */
6. public static void bubbleSort(int[] array) {
6. if (array == null || array.length <= 1) {
6. return;
6. }
6.int length = array.length;
6.// 外层循环控制比较轮数i
6. for (int i = 0; i < length; i++) {
6. // 内层循环控制每一轮比较次数,每进行一轮排序都会找出一个较大值
6. // (array.length - 1)防止索引越界,(array.length - 1 - i)减少比较次数
6. for (int j = 0; j < length - 1 - i; j++) {
6. // 前面的数大于后面的数就进行交换
6. if (array[j] > array[j + 1]) {
6. int temp = array[j + 1];
6. array[j + 1] = array[j];
6. array[j] = temp;
6. }
6. }
6. }
6.}
| | —- |
选择排序
- 时间复杂度:
- 最佳情况:T(n) = O(n2)
- 最差情况:T(n) = O(n2)
- 平均情况:T(n) = O(n2)
- 算法描述:n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
- 初始状态:无序区为R[1…n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
- 动图演示:
- 代码实现:
| /
Description: 选择排序
@param array
@return void
@author JourWon
@date 2019/7/11 23:31
*/
public static void selectionSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int length = array.length;
for (int i = 0; i < length - 1; i++) {
// 保存最小数的索引
int minIndex = i;
for (int j = i + 1; j < length; j++) {
// 找到最小的数
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
// 交换元素位置
if (i != minIndex) {
swap(array, minIndex, i);
}
}
}
/
Description: 交换元素位置
@param array
@param a
@param b
@return void
@author JourWon
@date 2019/7/11 17:57
*/
private static void swap(int[] array, int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
| | —- |
快速排序:
- 时间复杂度:
- 最佳情况:T(n) = O(nlogn)
- 最差情况:T(n) = O(n2)
- 平均情况:T(n) = O(nlogn)
- 算法描述:快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
- 动图演示:
- 代码实现:
| /*
Description: 快速排序
@param array
@return void
@author JourWon
@date 2019/7/11 23:39
/
public static void quickSort(int[] array) {
quickSort(array, 0, array.length - 1);
}
private static void quickSort(int[] array, int left, int right) {
if (array == null || left >= right || array.length <= 1) {
return;
}
int mid = partition(array, left, right);
quickSort(array, left, mid);
quickSort(array, mid + 1, right);
}
private static int partition(int[] array, int left, int right) {
int temp = array[left];
while (right > left) {
// 先判断基准数和后面的数依次比较
while (temp <= array[right] && left < right) {
—right;
}
// 当基准数大于了 arr[left],则填坑
if (left < right) {
array[left] = array[right];
++left;
}
// 现在是 arr[right] 需要填坑了
while (temp >= array[left] && left < right) {
++left;
}
if (left < right) {
array[right] = array[left];
—right;
}
}
array[left] = temp;
return left;
} | | —- |
二分查找
- 时间复杂度:O(h)=O(log2n)
- 二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法,前提是数据结构必须先排好序,时间复杂度可以表示O(h)=O(log2n),以2为底,n的对数。其缺点是要求待查表为有序表,且插入删除困难。
- 中值选取:
- 算法一: mid = (low + high) / 2
- 算法二: mid = low + (high – low)/2
- 动图演示:
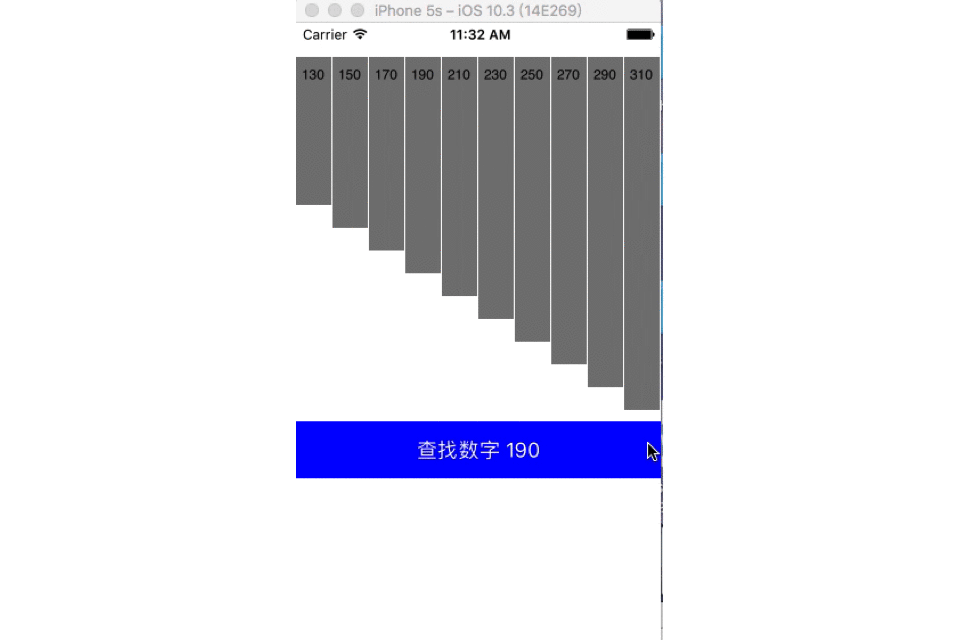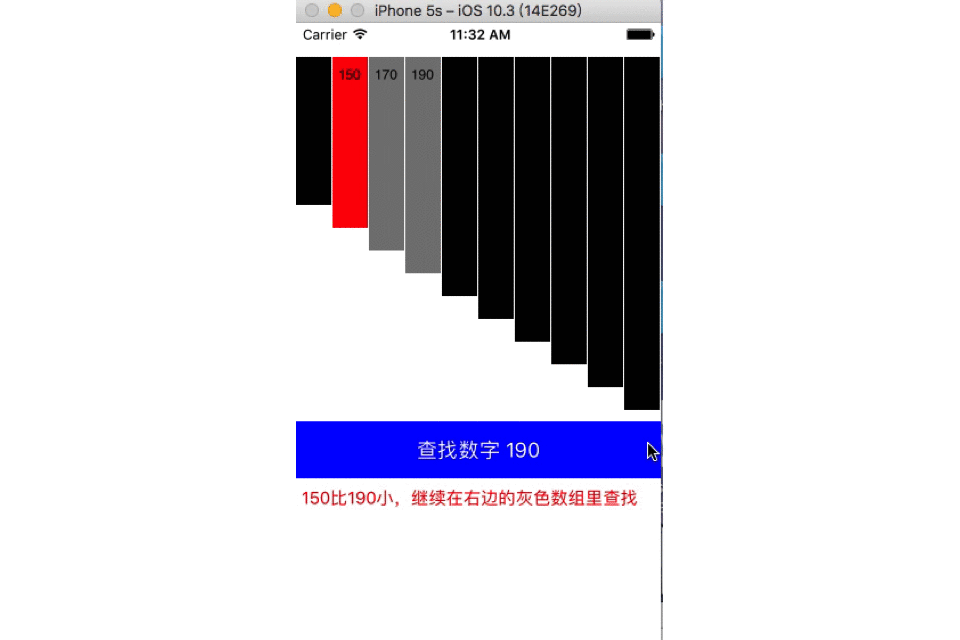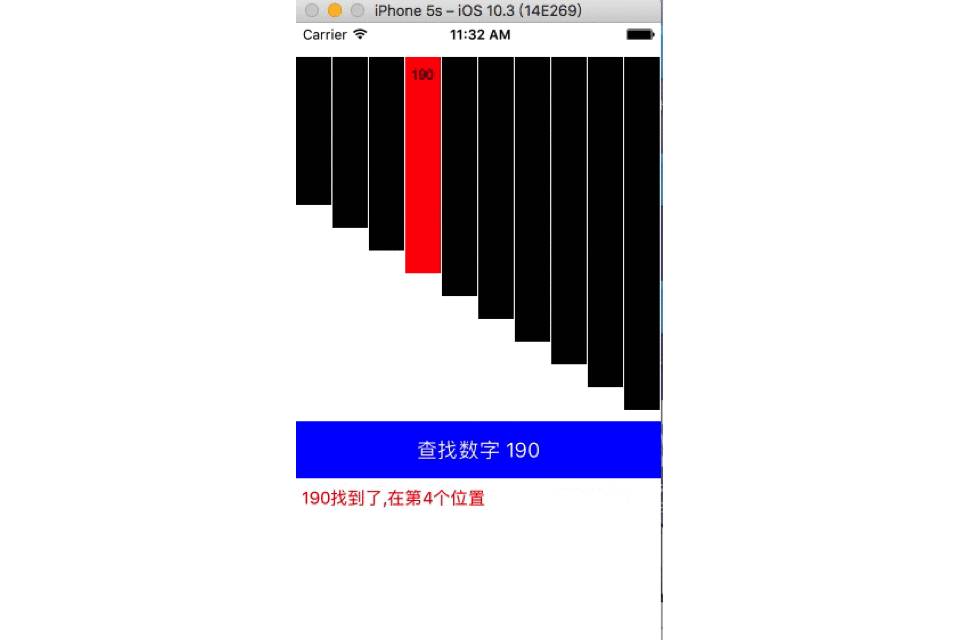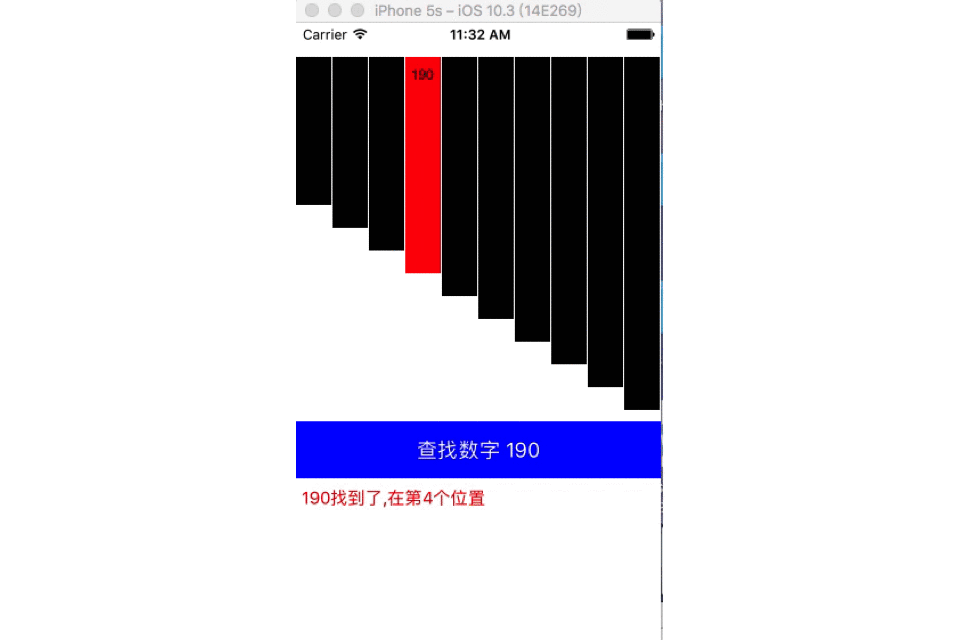
- 代码实现:
| public class BinarySearch { public static void main(String[] args) { int[] arr = {5, 12, 23, 43, 66, 98, 100}; System.out.println(binarySort(arr, 23)); } /* 循环实现二分查找 @param arr @param key @return */ public static int binarySearch(int[] arr, int key) { //第一个下标 int low = 0; //最后一个下标 int high = arr.length - 1; int mid = 0; //防越界 if (key < arr[low] || key > arr[high] || low > high) { return -1; } while (low <= high) { mid = (low + high) >>> 1; if (key < arr[mid]) { high = mid - 1; } else if (key > arr[mid]) { low = mid + 1; } else { return mid; } } return -1; } } |
|---|
递归
- 前提调教
- 有反复执行的过程(调用自身)
- 有跳出反复执行过程的条件(递归出口)
- 工作原理:
- 递归函数就是直接或间接调用自身的函数,也就是自身调用自己。
- 代码实例:
| 递归阶乘n! = n (n-1) (n-2) … 1(n>0)
public static Integer recursionMulity(Integer n) {
if (n == 1) {
return 1;
}
return n * recursionMulity(n - 1);
} | | —- |
[