估计大家对 JS 数组的sort 方法已经不陌生了，之前也对它的用法做了详细的总结。那，它的内部是如何来实现的呢？如果说我们能够进入它的内部去看一看，
理解背后的设计，会使我们的思维和素养得到不错的提升。

sort 方法在 V8 内部相对与其他方法而言是一个比较高深的算法，对于很多边界情况做了反复的优化，但是这里我们不会直接拿源码来干讲。我们会来根据源码的思路，实现一个
跟引擎性能一样的排序算法，并且一步步拆解其中的奥秘。

V8 引擎的思路分析

首先大概梳理一下源码中排序的思路:

设要排序的元素个数是n：

  • 当 n <= 10 时，采用插入排序
  • 当 n > 10 时，采用三路快速排序
    • 10 < n <= 1000, 采用中位数作为哨兵元素
    • n > 1000, 每隔 200~215 个元素挑出一个元素，放到一个新数组，然后对它排序，找到中间位置的数，以此作为中位数

在动手之前，我觉得我们有必要为什么这么做搞清楚。

第一、为什么元素个数少的时候要采用插入排序？

虽然插入排序理论上说是O(n^2)的算法，快速排序是一个O(nlogn)级别的算法。但是别忘了，这只是理论上的估算，在实际情况中两者的算法复杂度前面都会有一个系数的，
当 n 足够小的时候，快速排序nlogn的优势会越来越小，倘若插入排序O(n^2)前面的系数足够小，那么就会超过快排。而事实上正是如此，插入排序经过优化以后对于小数据集的排序会有非常优越的性能，很多时候甚至会超过快排。

因此，对于很小的数据量，应用插入排序是一个非常不错的选择。

第二、为什么要花这么大的力气选择哨兵元素？

因为快速排序的性能瓶颈在于递归的深度，最坏的情况是每次的哨兵都是最小元素或者最大元素，那么进行partition(一边是小于哨兵的元素，另一边是大于哨兵的元素)时，就会有一边是空的，那么这么排下去，递归的层数就达到了n, 而每一层的复杂度是O(n)，因此快排这时候会退化成O(n^2)级别。

这种情况是要尽力避免的！如果来避免？

就是让哨兵元素进可能地处于数组的中间位置，让最大或者最小的情况尽可能少。这时候，你就能理解 V8 里面所做的种种优化了。

接下来，我们来一步步实现的这样的官方排序算法。

插入排序及优化

最初的插入排序可能是这样写的:

  1. const insertSort = (arr, start = 0, end) => {
  2.   end = end || arr.length;
  3.   for(let i = start; i < end; i++) {
  4.     let j;
  5.     for(j = i; j > start && arr[j - 1] > arr[j]; j --) {
  6.       let temp = arr[j];
  7.       arr[j] = arr[j - 1];
  8.       arr[j - 1] = temp;
  9.     }
  10.   }
  11.   return;
  12. }

看似可以正确的完成排序，但实际上交换元素会有相当大的性能消耗，我们完全可以用变量覆盖的方式来完成，如图所示: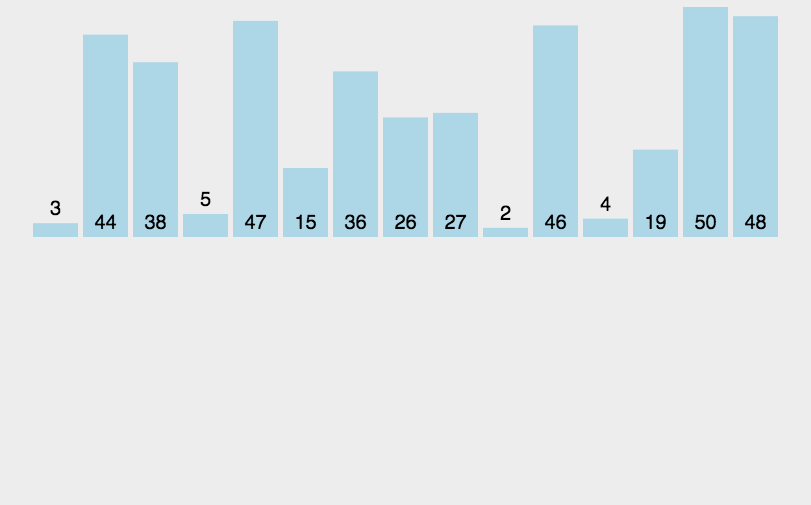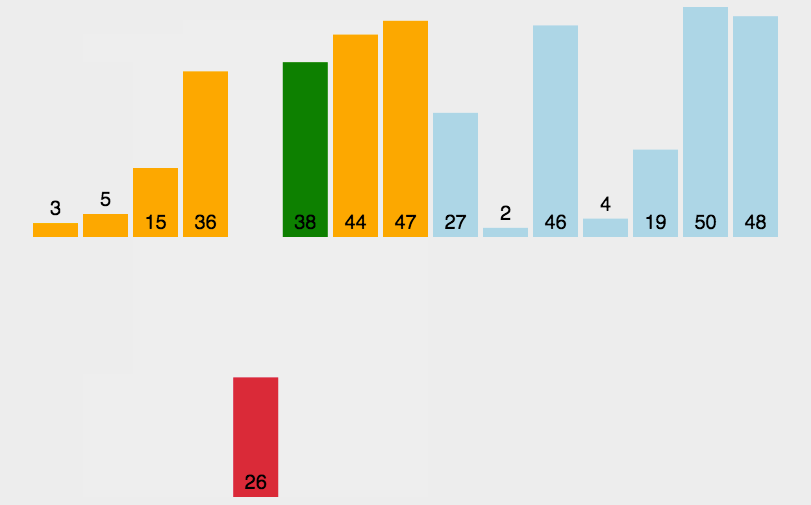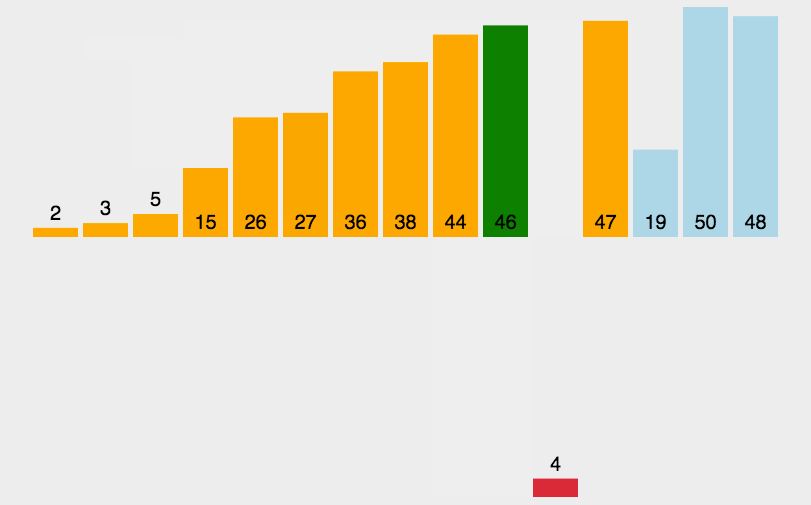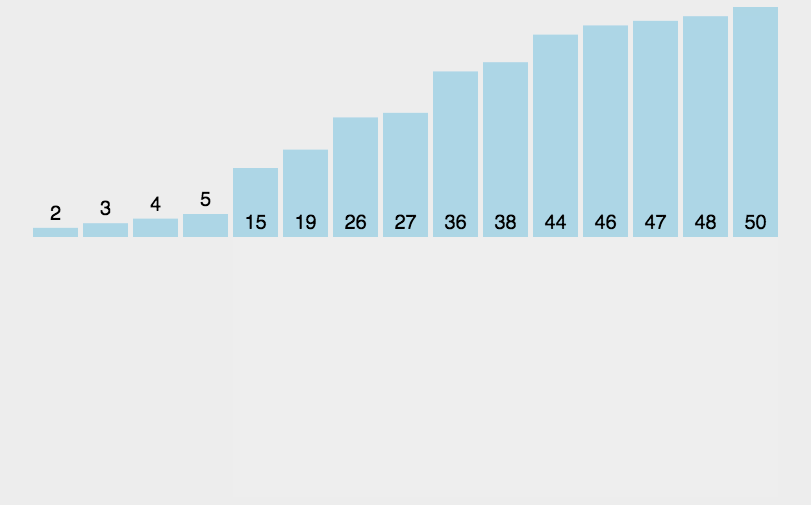
1.gif
优化后代码如下:

  1. const insertSort = (arr, start = 0, end) => {
  2.   end = end || arr.length;
  3.   for(let i = start; i < end; i++) {
  4.     let e = arr[i];
  5.     let j;
  6.     for(j = i; j > start && arr[j - 1] > e; j --)
  7.       arr[j] = arr[j-1];
  8.     arr[j] = e;
  9.   }
  10.   return;
  11. }

接下来正式进入到 sort 方法。

寻找哨兵元素

sort的骨架大致如下:

  1. Array.prototype.sort = (comparefn) => {
  2.   let array = Object(this);
  3.   let length = array.length >>> 0;
  4.   return InnerArraySort(array, length, comparefn);
  5. }
  7. const InnerArraySort = (array, length, comparefn) => {
  8.   // 比较函数未传入
  9.   if (Object.prototype.toString.call(callbackfn) !== "[object Function]") {
  10.     comparefn = function (x, y) {
  11.       if (x === y) return 0;
  12.       x = x.toString();
  13.       y = y.toString();
  14.       if (x == y) return 0;
  15.       else return x < y ? -1 : 1;
  16.     };
  17.   }
  18.   const insertSort = () => {
  19.     //...
  20.   }
  21.   const getThirdIndex = (a, from, to) => {
  22.     // 元素个数大于1000时寻找哨兵元素
  23.   }
  24.   const quickSort = (a, from, to) => {
  25.     //哨兵位置
  26.     let thirdIndex = 0;
  27.     while(true) {
  28.       if(to - from <= 10) {
  29.         insertSort(a, from, to);
  30.         return;
  31.       }
  32.       if(to - from > 1000) {
  33.         thirdIndex = getThirdIndex(a, from , to);
  34.       }else {
  35.         // 小于1000 直接取中点
  36.         thirdIndex = from + ((to - from) >> 2);
  37.       }
  38.     }
  39.     //下面开始快排
  40.   }
  41. }

我们先来把求取哨兵位置的代码实现一下:

  1. const getThirdIndex = (a, from, to) => {
  2.   let tmpArr = [];
  3.   // 递增量，200~215 之间，因为任何正数和15做与操作，不会超过15，当然是大于0的
  4.   let increment = 200 + ((to - from) & 15);
  5.   let j = 0;
  6.   from += 1;
  7.   to -= 1;
  8.   for (let i = from; i < to; i += increment) {
  9.     tmpArr[j] = [i, a[i]];
  10.     j++;
  11.   }
  12.   // 把临时数组排序，取中间的值，确保哨兵的值接近平均位置
  13.   tmpArr.sort(function(a, b) {
  14.     return comparefn(a[1], b[1]);
  15.   });
  16.   let thirdIndex = tmpArr[tmpArr.length >> 1][0];
  17.   return thirdIndex;
  18. }

完成快排

接下来我们来完成快排的具体代码：

  1. const _sort = (a, b, c) => {
  2.   let arr = [a, b, c];
  3.   insertSort(arr, 0, 3);
  4.   return arr;
  5. }
  7. const quickSort = (a, from, to) => {
  8.   //...
  9.   // 上面我们拿到了thirdIndex
  10.   // 现在我们拥有三个元素，from, thirdIndex, to
  11.   // 为了再次确保 thirdIndex 不是最值，把这三个值排序
  12.   [a[from], a[thirdIndex], a[to - 1]] = _sort(a[from], a[thirdIndex], a[to - 1]);
  13.   // 现在正式把 thirdIndex 作为哨兵
  14.   let pivot = a[thirdIndex];
  15.   [a[from], a[thirdIndex]] = [a[thirdIndex], a[from]];
  16.   // 正式进入快排
  17.   let lowEnd = from + 1;
  18.   let highStart = to - 1;
  19.   a[thirdIndex] = a[lowEnd];
  20.   a[lowEnd] = pivot;
  21.   // [lowEnd, i)的元素是和pivot相等的
  22.   // [i, highStart) 的元素是需要处理的
  23.   for(let i = lowEnd + 1; i < highStart; i++) {
  24.     let element = a[i];
  25.     let order = comparefn(element, pivot);
  26.     if (order < 0) {
  27.       a[i] = a[lowEnd];
  28.       a[lowEnd] = element;
  29.       lowEnd++;
  30.     } else if(order > 0) {
  31.       do{
  32.         highStart--;
  33.         if(highStart === i) break;
  34.         order = comparefn(a[highStart], pivot);
  35.       }while(order > 0)
  36.       // 现在 a[highStart] <= pivot
  37.       // a[i] > pivot
  38.       // 两者交换
  39.       a[i] = a[highStart];
  40.       a[highStart] = element;
  41.       if(order < 0) {
  42.         // a[i] 和 a[lowEnd] 交换
  43.         element = a[i];
  44.         a[i] = a[lowEnd];
  45.         a[lowEnd] = element;
  46.         lowEnd++;
  47.       }
  48.     }
  49.   }
  50.   // 永远切分大区间
  51.   if (lowEnd - from > to - highStart) {
  52.     // 继续切分lowEnd ~ from 这个区间
  53.     to = lowEnd;
  54.     // 单独处理小区间
  55.     quickSort(a, highStart, to);
  56.   } else if(lowEnd - from <= to - highStart) {
  57.     from = highStart;
  58.     quickSort(a, from, lowEnd);
  59.   }
  60. }

测试结果

测试结果如下:

一万条数据:

1.jpg

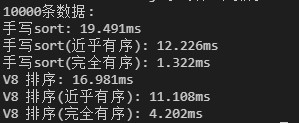
十万条数据:

2.jpg

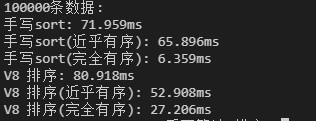
一百万条数据:

3.jpg

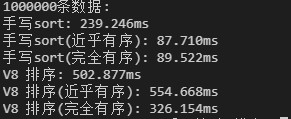
一千万条数据:

4.jpg

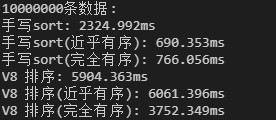
结果仅供大家参考，因为不同的node版本对于部分细节的实现可能不一样，我现在的版本是v10.15。

从结果可以看到，目前版本的 node 对于有序程度较高的数据是处理的不够好的，而我们刚刚实现的排序通过反复确定哨兵的位置就能
有效的规避快排在这一场景下的劣势。

最后给大家完整版的sort代码:

  1. const sort = (arr, comparefn) => {
  2.   let array = Object(arr);
  3.   let length = array.length >>> 0;
  4.   return InnerArraySort(array, length, comparefn);
  5. }
  7. const InnerArraySort = (array, length, comparefn) => {
  8.   // 比较函数未传入
  9.   if (Object.prototype.toString.call(comparefn) !== "[object Function]") {
  10.     comparefn = function (x, y) {
  11.       if (x === y) return 0;
  12.       x = x.toString();
  13.       y = y.toString();
  14.       if (x == y) return 0;
  15.       else return x < y ? -1 : 1;
  16.     };
  17.   }
  18.   const insertSort = (arr, start = 0, end) => {
  19.     end = end || arr.length;
  20.     for (let i = start; i < end; i++) {
  21.       let e = arr[i];
  22.       let j;
  23.       for (j = i; j > start && comparefn(arr[j - 1], e) > 0; j--)
  24.         arr[j] = arr[j - 1];
  25.       arr[j] = e;
  26.     }
  27.     return;
  28.   }
  29.   const getThirdIndex = (a, from, to) => {
  30.     let tmpArr = [];
  31.     // 递增量，200~215 之间，因为任何正数和15做与操作，不会超过15，当然是大于0的
  32.     let increment = 200 + ((to - from) & 15);
  33.     let j = 0;
  34.     from += 1;
  35.     to -= 1;
  36.     for (let i = from; i < to; i += increment) {
  37.       tmpArr[j] = [i, a[i]];
  38.       j++;
  39.     }
  40.     // 把临时数组排序，取中间的值，确保哨兵的值接近平均位置
  41.     tmpArr.sort(function (a, b) {
  42.       return comparefn(a[1], b[1]);
  43.     });
  44.     let thirdIndex = tmpArr[tmpArr.length >> 1][0];
  45.     return thirdIndex;
  46.   };
  48.   const _sort = (a, b, c) => {
  49.     let arr = [];
  50.     arr.push(a, b, c);
  51.     insertSort(arr, 0, 3);
  52.     return arr;
  53.   }
  55.   const quickSort = (a, from, to) => {
  56.     //哨兵位置
  57.     let thirdIndex = 0;
  58.     while (true) {
  59.       if (to - from <= 10) {
  60.         insertSort(a, from, to);
  61.         return;
  62.       }
  63.       if (to - from > 1000) {
  64.         thirdIndex = getThirdIndex(a, from, to);
  65.       } else {
  66.         // 小于1000 直接取中点
  67.         thirdIndex = from + ((to - from) >> 2);
  68.       }
  69.       let tmpArr = _sort(a[from], a[thirdIndex], a[to - 1]);
  70.       a[from] = tmpArr[0]; a[thirdIndex] = tmpArr[1]; a[to - 1] = tmpArr[2];
  71.       // 现在正式把 thirdIndex 作为哨兵
  72.       let pivot = a[thirdIndex];
  73.       [a[from], a[thirdIndex]] = [a[thirdIndex], a[from]];
  74.       // 正式进入快排
  75.       let lowEnd = from + 1;
  76.       let highStart = to - 1;
  77.       a[thirdIndex] = a[lowEnd];
  78.       a[lowEnd] = pivot;
  79.       // [lowEnd, i)的元素是和pivot相等的
  80.       // [i, highStart) 的元素是需要处理的
  81.       for (let i = lowEnd + 1; i < highStart; i++) {
  82.         let element = a[i];
  83.         let order = comparefn(element, pivot);
  84.         if (order < 0) {
  85.           a[i] = a[lowEnd];
  86.           a[lowEnd] = element;
  87.           lowEnd++;
  88.         } else if (order > 0) {
  89.           do{
  90.             highStart--;
  91.             if (highStart === i) break;
  92.             order = comparefn(a[highStart], pivot);
  93.           }while (order > 0) ;
  94.           // 现在 a[highStart] <= pivot
  95.           // a[i] > pivot
  96.           // 两者交换
  97.           a[i] = a[highStart];
  98.           a[highStart] = element;
  99.           if (order < 0) {
  100.             // a[i] 和 a[lowEnd] 交换
  101.             element = a[i];
  102.             a[i] = a[lowEnd];
  103.             a[lowEnd] = element;
  104.             lowEnd++;
  105.           }
  106.         }
  107.       }
  108.       // 永远切分大区间
  109.       if (lowEnd - from > to - highStart) {
  110.         // 单独处理小区间
  111.         quickSort(a, highStart, to);
  112.         // 继续切分lowEnd ~ from 这个区间
  113.         to = lowEnd;
  114.       } else if (lowEnd - from <= to - highStart) {
  115.         quickSort(a, from, lowEnd);
  116.         from = highStart;
  117.       }
  118.     }
  119.   }
  120.   quickSort(array, 0, length);
  121. }

参考链接:

V8 sort源码(点开第997行)

冴羽排序源码专题

三元博客