信息存储与运算
大小端记法:
例如,假设 个类型为 int 的变量 的地址 0x00, 也就是说,地址表达式 &x 的值为 0x00, 。那么(假设数据类型int 为 32 位表示) 节将被存储在内存的 0x00, 0x01, 0x02, 0x03 位置。

位运算
- 与 And:
A=1且B=1时,A&B = 1 - 或 Or:
A=1或B=1时,A|B = 1 - 非 Not:
A=1时,~A=0;A=0时,~A=1 - 异或 Exclusive-Or(Xor):
A=1或B=1时,A^B = 1;A=1且B=1时,A^B = 0
逻辑运算
- || 或运算:两个条件任意一个成立,即条件成立
- && 与运算:两个条件都成立,即条件成立。(比如:a&&b,如果判断a是false,则不会继续判断b,直接返回false)
- !非运算:
A=1时,~A=0;A=0时,~A=1
整数表示与运算
整数符号
signed 和 unsigned,表示有符号数和无符号数。有符号数和无符号数的区别主要在于有没有最高位的符号位,以及由此带来的计算方式的不同。符号位中,0 表示非负数,1 表示负数。
对于二进制数字来说,还有两种常用操作:左移和右移。
- 左移比较简单,在右边补 0 即可。
- 右移的话有两种类型,一种是逻辑右移(左边补 0),另一种是算术右移(左边补符号位)。
类型转换
在进行有符号和无符号数的互相转换时:
- 具体每一个字节的值不会改变,改变的是计算机解释当前值的方式(是否解释为符号位,但是位数跟值都不会改变)
- 如果一个表达式既包含有符号数也包含无符号数,那么会被隐式转换成无符号数进行比较
类型扩展和截断
- 扩展:(从少字节的数据类型扩展为多字节的数据类型时,值一般不变)
- 无符号数:加 0
- 有符号数:加符号位
- 截取:(对于小的数字进行截断时可以得到预期的结果,而对于大的数字则有概率遗失部分值)
- 无符号数:mod 操作
- 有符号数: mod 操作后再转换为有符号数
加减溢出
- 【无符号数】加法:如果两个
N位的数字相加,结果是N+1位的话,由于没办法表示
“进一”(位数限制的原因),最高位的“1”会被丢弃,这就是溢出。 - 【有符号数】加法:分为正溢出和负溢出,操作大体上跟【无符号数】类似,也很好分辨:正溢出就是数值进1把原来为 0 的符号位修改成了 1,反而成了负数;负溢出是数值太小,把原来为 1 的符号位修改成了 0,反而成了正数。
无符号数溢出的值表示如下:
有符号数溢出的值表示如下: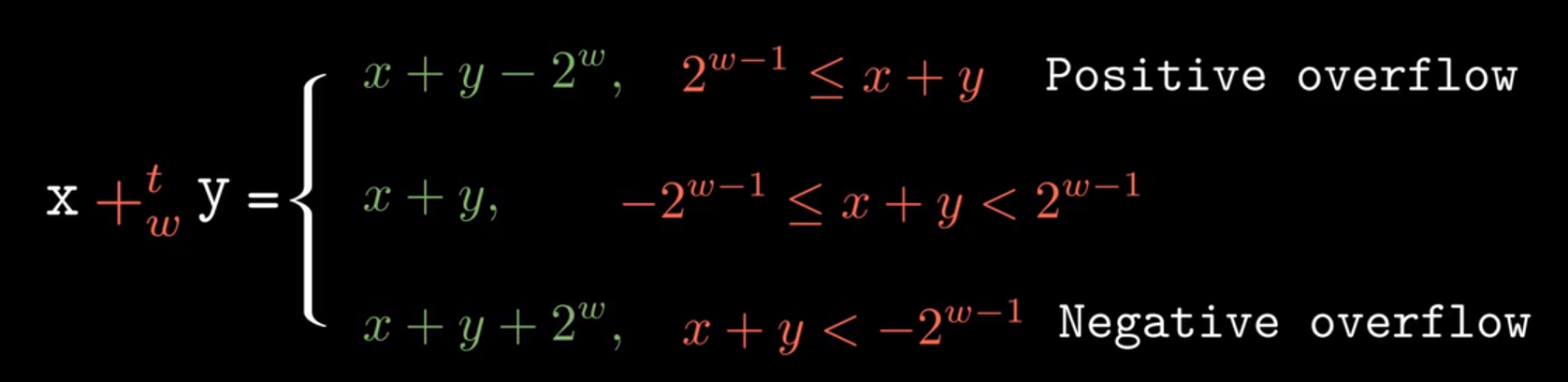
检查溢出: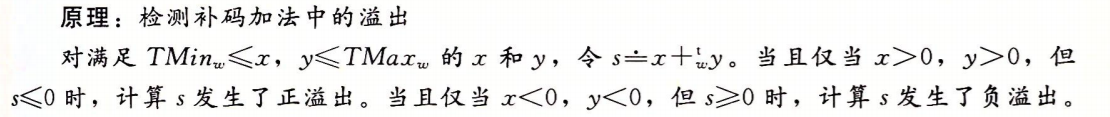
乘除溢出
无符号进行乘法操作时,忽略最高的 w 位,结果会等于乘后再 mod 【2的w次方】
乘法操作如下(利用左移实现):
除法操作则是用右移实现:
- 类似乘法,逆操作嘛
- 对于有符号数,是“算术右移”
- 发现除不尽时,总是向0的方向进行舍入(视情况而定,精确度不准)
加法逆元
其实就是相反数。一个数x加上 -x,得到0,这就是加法逆元。
但是无符号数都是>0的,这所谓的-x该如何表示呢?
举个简单的例子就知道了:
- 我们前面讨论过溢出的情况,也就是会使结果等于0
所以x的加法逆元则有: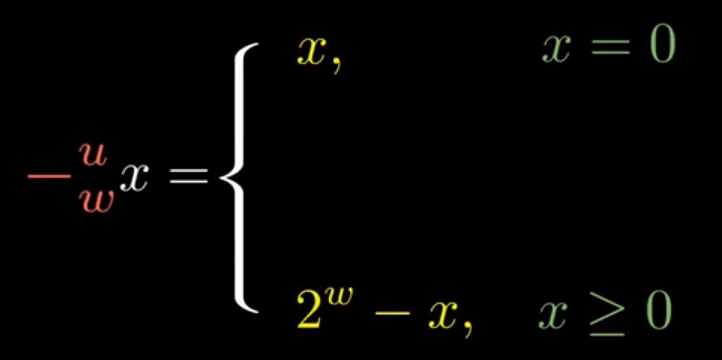
有符号数的逆元就比较容易了(直接就是 -x):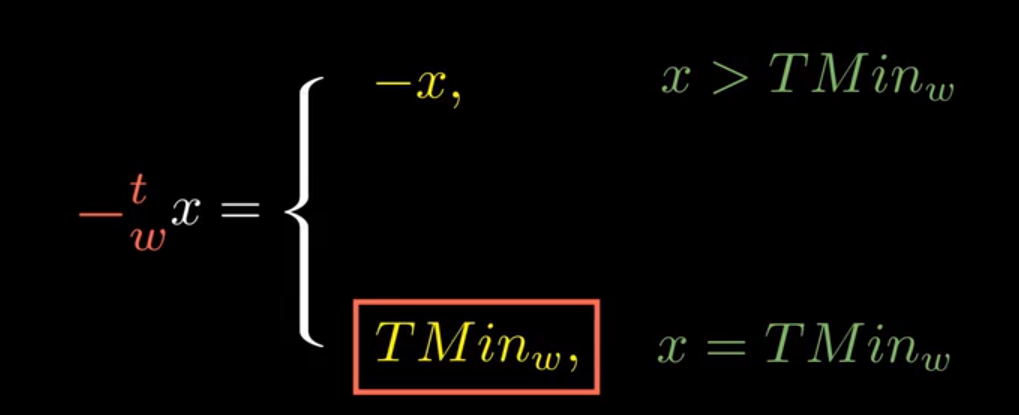
- 注意TMin与Tmax是非对称的,所以需要通过负溢出来实现,简单来说,Tmin的逆元就是他自己。
浮点数
IEEE的浮点公式:

浮点数的位数表示:

其中 s 对应着符号位,exp 对应着 E,frac 对应着 M
四种浮点数:

对应到数轴上是这样的:
舍入
对于浮点数的加法和乘法来说,我们可以先计算出准确值,然后转换到合适的精度。
有这几种舍入方法:
- 向上/向下舍入
- 向零舍入
- 向偶数舍入
小知识:
- 浮点数的运算并不具备分配性

- int、float、double之间的强制转换可能会导致“溢出”、“无法保留精度”等问题

