排序算法分类

比较类排序

通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 O(nlogn)，因此也称为非线性时间比较类排序。

非比较类排序

不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

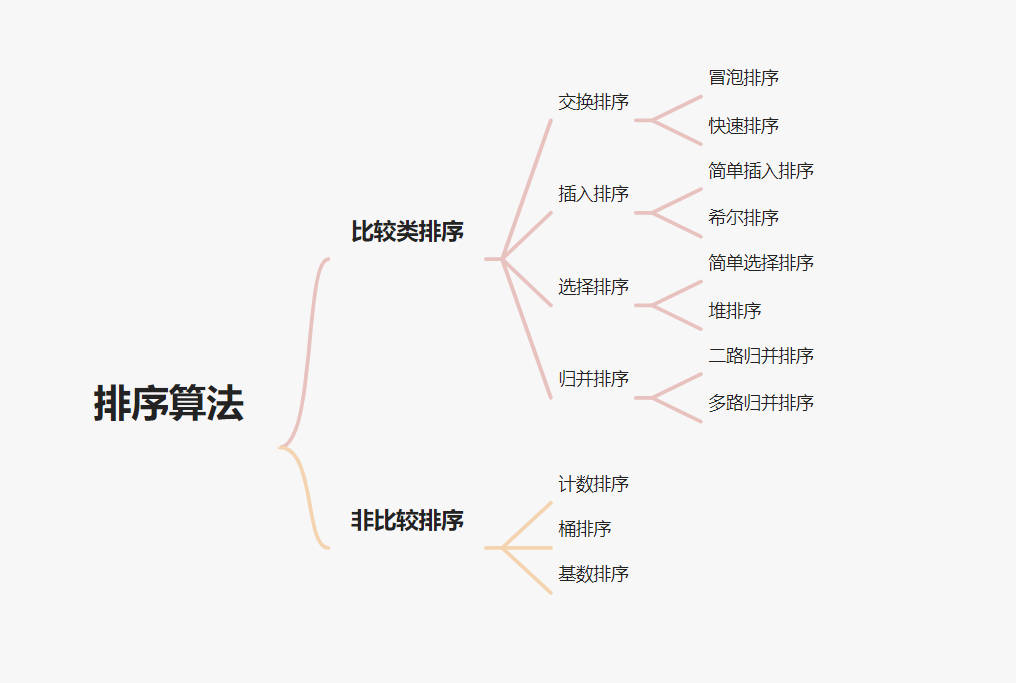
sort.png

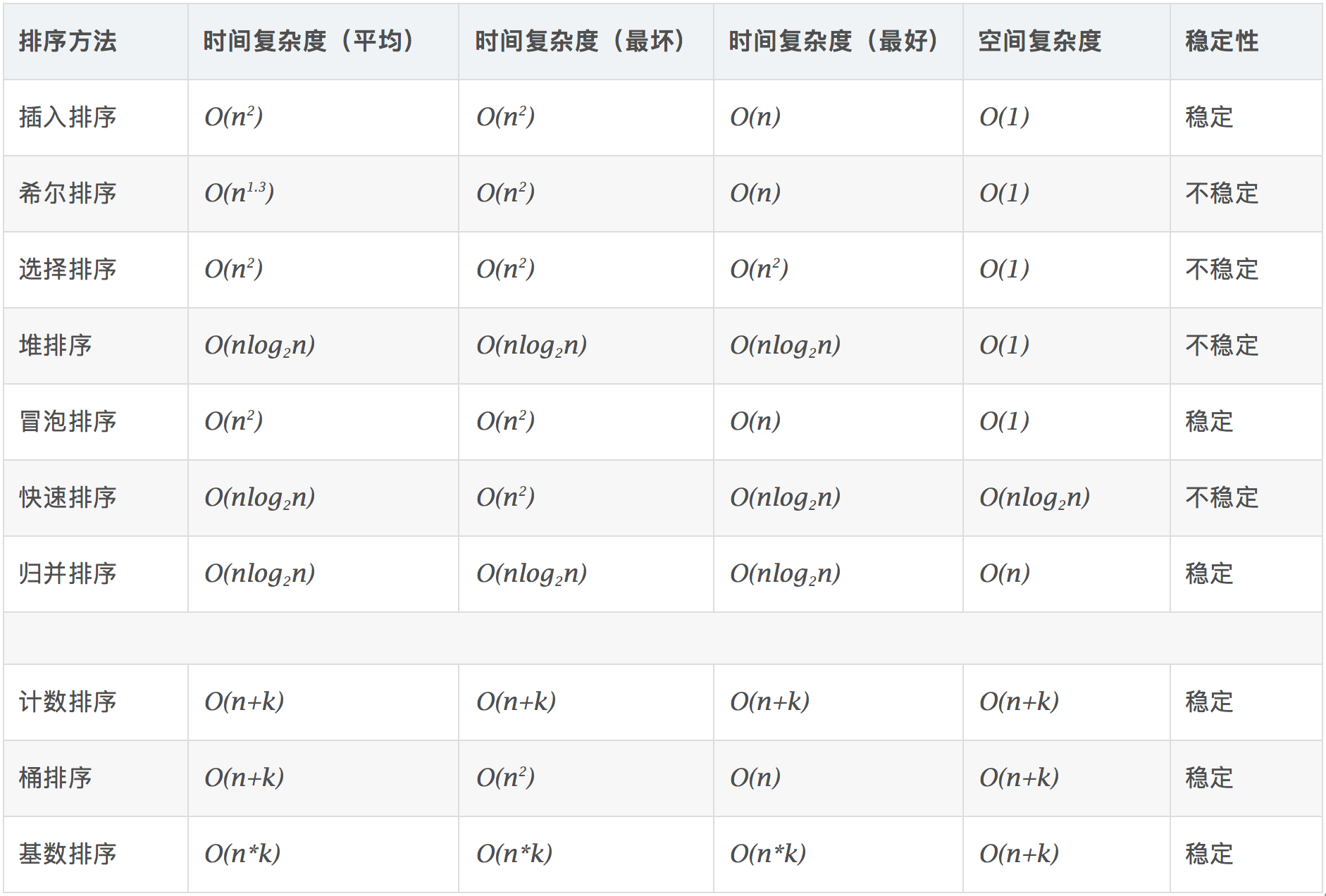
sort_compare.png

重点看堆排序、快速排序、归并排序，面试通常会考 O(nlogn) 的排序。

排序动画

初级排序 O(n^2)

选择排序（Selection Sort）

每次选最小值，然后放到待排序数组的起始位置。

  1. function selectionSort (arr) {
  2.   const len = arr.length;
  3.   let minIdx, temp;
  5.   for (let i = 0; i < len - 1; i++) {
  6.     minIdx = i;
  8.     for (let j = i + 1; j < len; j++) {
  9.       if (arr[j] < arr[minIdx]) {
  10.         minIdx = j;
  11.       }
  12.     }
  14.     temp = arr[i];
  15.     arr[i] = arr[minIdx];
  16.     arr[minIdx] = temp;
  17.   }
  19.   return arr;
  20. }

插入排序（Insertion Sort）

从前到后逐步构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

  1. function insertionSort (arr) {
  2.   const len = arr.length;
  3.   let preIdx, current;
  5.   for (let i = 1; i < len; i++) {
  6.     preIdx = i - 1;
  7.     current = arr[i];
  9.     while (preIdx >= 0 && arr[preIdx] > current) {
  10.       arr[preIdx + 1] = arr[preIdx];
  11.       preIdx--;
  12.     }
  14.     arr[preIdx + 1] = current;
  15.   }
  17.   return arr;
  18. }

冒泡排序（Bubble Sort）

嵌套循环，每次查看相邻的元素如果逆序，则交换。

  1. function bubbleSort (arr) {
  2.   const len = arr.length;
  4.   let temp, finish;
  6.   for (let i = 0; i < len - 1; i++) {
  7.     finish = true;
  9.     for (let j = 0; j < len - 1 - i; j++) {
  10.       if (arr[j] > arr[j + 1]) {
  11.         temp = arr[j + 1];
  12.         arr[j + 1] = arr[j];
  13.         arr[j] = temp;
  15.         finish = false;
  16.       }
  17.     }
  19.     if (finish) break;
  20.   }
  22.   return arr;
  23. }

高级排序 O(N*LogN)

快速排序（Quick Sort）

数组取标杆 pivot，将小元素放到 pivot 左边，大元素放右侧，然后依次对左边和右边的子数组继续快排。以达到整个序列有序。

pivot 可以选在任意位置，左边、中间、右边。

  1. function partition (arr, start, end) {
  2.   const pivot = end;
  4.   let counter = start;
  6.   for (let i = start; i < end; i++) {
  7.     if (arr[i] < arr[pivot]) {
  8.       if (counter == i) {
  9.         counter++;
  10.       } else {
  11.         const temp = arr[counter];
  12.         arr[counter] = arr[i];
  13.         arr[i] = temp;
  14.         counter++;
  15.       }
  16.     }
  17.   }
  19.   const temp = arr[pivot];
  20.   arr[pivot] = arr[counter];
  21.   arr[counter] = temp;
  23.   return counter;
  24. }
  26. function quickSort (arr, begin, end) {
  27.   if (end < begin) return;
  29.   const pivot = partition(arr, begin, end);
  31.   quickSort(arr, begin, pivot - 1);
  32.   quickSort(arr, pivot + 1, end);
  33. }

归并排序（Merge Sort）

  • 把长度为 n 的输入序列分成两个长度为 n / 2 的子序列；
  • 对这两个子序列分别采用归并排序；
  • 将两个排序好的子序列合并成一个最终的排序序列。
  1. function merge (arr, left, mid, right) {
  2.   const temp = new Array(right - left + 1);
  4.   let i = left,
  5.       j = mid + 1,
  6.       k = 0;
  8.   while (i <= mid && j <= right) {
  9.     temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
  10.   }
  12.   while (i <= mid) temp[k++] = arr[i++];
  13.   while (j <= right) temp[k++] = arr[j++];
  15.   for (i = 0; i < temp.length; i++) {
  16.     arr[left + i] = temp[i];
  17.   }
  18. }
  20. function mergeSort (arr, left, right) {
  21.   if (right <= left) return;
  23.   const mid = (left + right) >> 1;
  25.   mergeSort(arr, left, mid);
  26.   mergeSort(arr, mid + 1, right);
  28.   merge(arr, left, mid, right);
  29. }

堆排序（Heap Sort）

堆插入 O(logN)，取最大值/最小值 O(1)。

  • 数组元素依次建立小顶堆
  • 依次取堆顶元素，并删除
  1. class Heap {
  2.   constructor (arr) {
  3.     this.len = arr.length;
  5.     for (let i = Math.floor(this.len / 2); i >= 0; i--) {
  6.       this.heapify(arr, i);
  7.     }
  8.   }
  10.   heapify (arr, i) {
  11.     let left = 2 * i + 1,
  12.         right = 2 * i + 2,
  13.         largest = i;
  15.     if (left < this.len && arr[left] > arr[largest]) {
  16.       largest = left;
  17.     }
  18.     if (right < this.len && arr[right] > arr[largest]) {
  19.       largest = right;
  20.     }
  22.     if (largest != i) {
  23.       this.swap(arr, i, largest);
  24.       this.heapify(arr, largest);
  25.     }
  26.   }
  28.   swap (arr, i, j) {
  29.     const temp = arr[i];
  30.     arr[i] = arr[j];
  31.     arr[j] = temp;
  32.   }
  33. }
  36. function heapSort (arr) {
  37.   const heap = new Heap(arr);
  39.   for (let i = arr.length - 1; i > 0; i--) {
  40.     heap.swap(arr, 0, i);
  41.     heap.len--;
  42.     heap.heapify(arr, 0);
  43.   }
  44. }

总结

归并和快排具有相似性，但步骤顺序相反。

归并排序：先排序左右子数组，然后合并两个有序子数组；
快速排序：先调配出左右子数组，然后对于左右子数组进行排序；

特殊排序 O(n)

计数排序（Counting Sort）

计数排序要求输入的数组必须是有确定范围的整数。
将输入的数据值转化为键存储在额外开辟的数组空间中，然后依次把计数大于 1 的填充回原数组。

  1. function countingSort (arr, maxVal) {
  2.   const bucket = new Array(maxVal + 1);
  4.   let sortedIndex = 0,
  5.       arrLen = arr.length,
  6.       bucketLen = bucket.length;
  8.   for (let i = 0; i < arrLen; i++) {
  9.     if (!bucket[arr[i]]) {
  10.       bucket[arr[i]] = 0;
  11.     }
  12.     bucket[arr[i]]++;
  13.   }
  15.   for (let j = 0; j < bucketLen; j++) {
  16.     while (bucket[j] > 0) {
  17.       arr[sortedIndex++] = j;
  18.       bucket[j]--;
  19.     }
  20.   }
  21. }

桶排序（Bucket Sort）

桶排序的工作原理：假设输入数据均匀分布，将数据分到有限的桶里，每个桶再分别排序（可能使用别的排序算法或者以递归方式继续使用桶排序）。

  1. function insertionSort (arr) {
  2.   const len = arr.length;
  3.   let preIdx, current;
  5.   for (let i = 1; i < len; i++) {
  6.     preIdx = i - 1;
  7.     current = arr[i];
  9.     while (preIdx >= 0 && arr[preIdx] > current) {
  10.       arr[preIdx + 1] = arr[preIdx];
  11.       preIdx--;
  12.     }
  14.     arr[preIdx + 1] = current;
  15.   }
  17.   return arr;
  18. }
  20. function bucketSort (arr, bucketSize) {
  21.   if (arr.length === 0) return [];
  23.   let i,
  24.       minVal = arr[0],
  25.       maxVal = arr[0];
  27.   for (i = 1; i < arr.length; i++) {
  28.     if (arr[i] < minVal) {
  29.       minVal = arr[i];
  30.     } else if (arr[i] > maxVal) {
  31.       maxVal = arr[i];
  32.     }
  33.   }
  36.   // 初始化桶
  37.   bucketSize = bucketSize || 5;
  39.   const bucketCount = Math.floor((maxVal - minVal) / bucketSize) + 1,
  40.         buckets = new Array(bucketCount);
  42.   for (i = 0; i < buckets.length; i++) {
  43.     buckets[i] = [];
  44.   }
  47.   // 利用映射函数分配数据
  48.   for (i = 0; i < arr.length; i++) {
  49.     buckets[Math.floor((arr[i] - minVal) / bucketSize)].push(arr[i]);
  50.   }
  53.   arr.length = 0;
  55.   for (i = 0; i < buckets.length; i++) {
  56.     insertionSort(buckets[i]); // 桶排序，使用插入排序
  58.     for (let j = 0; j < buckets[i].length; j++) {
  59.       arr.push(buckets[i][j]);
  60.     }
  61.   }
  62. }

基数排序（Radix Sort）

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。

  1. function radixSort (arr, maxDigit) {
  2.   const counter = [];
  4.   let mod = 10,
  5.       dev = 1;
  7.   for (let i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
  8.     for (let j = 0; j < arr.length; j++) {
  9.       const bucket = parseInt((arr[j] % mod) / dev);
  11.       if (counter[bucket] == null) counter[bucket] = [];
  13.       counter[bucket].push(arr[j]);
  14.     }
  16.     let pos = 0;
  18.     for (let j = 0; j < counter.length; j++) {
  19.       let val = null;
  21.       if (counter[j]) {
  22.         while ((val = counter[j].shift()) != null) {
  23.           arr[pos++] = val;
  24.         }
  25.       }
  26.     }
  27.   }
  28. }

相关题目

数组的相对排序

有效的字母异位词

合并区间

翻转对

  1. // 数组的相对排序
  3. // 计数排序
  4. /**
  5.  * @param {number[]} arr1
  6.  * @param {number[]} arr2
  7.  * @return {number[]}
  8.  */
  9. var relativeSortArray = function (arr1, arr2) {
  10.   const counts = new Array(1001).fill(0);
  12.   for (const n of arr1) {
  13.     counts[n]++;
  14.   }
  16.   const ans = [];
  18.   for (const n of arr2) {
  19.     while (counts[n] > 0) {
  20.       ans.push(n);
  21.       counts[n]--;
  22.     }
  23.   }
  25.   for (let i = 0; i < counts.length; i++) {
  26.     while (counts[i] > 0) {
  27.       ans.push(i);
  28.       counts[i]--;
  29.     }
  30.   }
  32.   return ans;
  33. };
  1. // 有效的字母异位词，可以使用快排和计数排序
  3. /**
  4.  * @param {string} s
  5.  * @param {string} t
  6.  * @return {boolean}
  7.  */
  8. var isAnagram = function(s, t) {
  9.   if (s.length != t.length) return false;
  11.   const map = new Map();
  13.   for (const i of s) {
  14.     map.set(i, s);
  15.   }
  16.   for (const i of t) {
  17.     if (!map.has(i)) return false;
  18.     map.delete(i);
  19.   }
  21.   return true;
  22. };
  1. // 合并区间
  3. /**
  4.  * @param {number[][]} intervals
  5.  * @return {number[][]}
  6.  */
  7. var merge = function(intervals) {
  8.   intervals.sort((a, b) => a[0] - b[0]);
  10.   const ans = [];
  12.   for (let i = 0; i < intervals.length; i++) {
  13.     const start = intervals[i][0];
  15.     let cur = intervals[i][1];
  17.     while(i < intervals.length-1 && cur >= intervals[i+1][0]) {
  18.       cur = Math.max(intervals[i+1][1], cur);
  19.       i++;
  20.     }
  22.     ans.push([start, cur]);
  23.   }
  25.   return ans;
  26. };
  1. // 翻转对
  3. var reversePairs = function(nums) {
  4.   if (nums.length === 0) return 0;
  5.   return reversePairsRecursive(nums, 0, nums.length - 1);
  6. };
  8. const reversePairsRecursive = (nums, left, right) => {
  9.   if (left === right) return 0;
  11.   const mid = Math.floor((left + right) / 2),
  12.         n1 = reversePairsRecursive(nums, left, mid),
  13.         n2 = reversePairsRecursive(nums, mid + 1, right);
  15.   let ret = n1 + n2,
  16.       i = left,
  17.       j = mid + 1;
  19.   while (i <= mid) {
  20.     while (j <= right && nums[i] > 2 * nums[j]) j++;
  22.     ret += j - mid - 1;
  23.     i++;
  24.   }
  26.   const sorted = new Array(right - left + 1);
  28.   let p1 = left,
  29.       p2 = mid + 1,
  30.       p = 0;
  32.   while (p1 <= mid || p2 <= right) {
  33.     if (p1 > mid) {
  34.       sorted[p++] = nums[p2++];
  35.     } else if (p2 > right) {
  36.       sorted[p++] = nums[p1++];
  37.     } else {
  38.       if (nums[p1] < nums[p2]) {
  39.         sorted[p++] = nums[p1++];
  40.       } else {
  41.         sorted[p++] = nums[p2++];
  42.       }
  43.     }
  44.   }
  46.   for (let k = 0; k < sorted.length; k++) {
  47.     nums[left + k] = sorted[k];
  48.   }
  50.   return ret;
  51. }