数据结构与算法本身解决的是两个问题：

  • 如何让代码运行得更快；
  • 如何让代码更省空间。

对于算法来说，执行效率是一个非常重要的考量指标。如何衡量编写的算法代码的执行效率？

这就牵扯到 2 个概念：时间复杂度分析、空间复杂度分析。

复杂度分析是算法学习的精髓，只要掌握了它，数据结构和算法的内容基本就掌握了一半。

为什么需要复杂度分析

你可能会问如果把代码跑一遍，通过统计、监控，就可以得到算法执行的时间和占用的内存大小。

那么为什么还需要做复杂度分析？

首先这种评估算法执行效率的方法是对的，它也有一个名字叫 事后统计法。

这种统计方法有非常大的局限性。

  • 测试结果非常依赖测试环境；
  • 测试结果收数据规模的影响很大；

我们需要一种不需要具体数据测试，就可以粗略估计算法的执行效率的方法。

这就是我们需要了解的时间、空间复杂度分析方法。

大 O 复杂度表示法

所有代码的执行时间 T(n) 与每行代码的执行次数 f(n) 成正比。

我们可以把这个规律总结成一个公式：

  1. T(n) = O(f(n));

T(n) 表示代码执行的时间，n 表示数据规模的大小。 f(n) 表示每行代码执行的次数总和。 O 表示代码执行时间 T(n) 与 f(n) 表达式成正比。

大 O 时间复杂度实并不具体表示代码的真正执行时间，而是表示代码执行时间随数据规模增长的变化趋势。

所以也被叫做渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

时间复杂度分析

分析一段代码的时间复杂度有三个比较实用的方法：

1. 只关注循环执行次数最多的一段代码

我们在分析一个算法、一段代码的时间复杂度时，只需要关注循环执行次数最多的那段代码即可。

  1. function cal (n) {
  2.   let sum = 0;
  4.   for (let i = 1; i <= n; i++) {
  5.     sum = sum + i;
  6.   }
  8.   return sum;
  9. }

比如上面这段代码，因为存在一个 for 循环，其中的代码被执行了 n 次，所以时间复杂度为 O(n)。

2. 加法法则：总复杂度等于量级最大的那段代码的复杂度

  1. function cal (n) {
  2.   let sum1 = 0;
  3.   for (let p = 1; p < 100; p++) {
  4.     sum1 = sum1 + p;
  5.   }
  7.   let sum2 = 0;
  8.   for (let q = 1; q < n; q++) {
  9.     sum2 = sum2 + q;
  10.   }
  12.   let sum3 = 0;
  13.   for (let i = 1; i <= n; i++) {
  14.     for (let j = 1; j <= n; j++) {
  15.       sum3 = sum3 + i * j;
  16.     }
  17.   }
  19.   return sum1 + sum2 + sum3;
  20. }

这段代码可以分为 3 部分，分别求 sum1、sum2、sum3。

我们可以分别分析每一部分的时间复杂度，然后把它们放到一起，再取一个量级最大的作为整段代码的复杂度。

第一段代码是一个常量的执行时间，跟 n 的规模无关。

尽管常量对代码的执行时间有很大影响，但是对于时间复杂度来说，它表示的是一个算法执行效率与数据规模增长的变化趋势，所以我们可以忽略掉常量的执行时间。它本身对于增长趋势并没有影响。

第二段代码和第三段代码的时间复杂度分别是 O(n) 和 O(n²)。

综合这三段代码的时间复杂度，我们取其中最大的量级，所以，这段代码的时间复杂度为 O(n²)。

也就是说，总的时间复杂度等于量级最大的那段代码的时间复杂度。

3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

我们可以把乘法法则看作嵌套循环。

  1. function cal (n) {
  2.   let ret = 0;
  4.   for (let i = 1; i <= n; i++) {
  5.     ret = ret + f(i);
  6.   }
  8.   return ret;
  9. }
  11. function f (n) {
  12.   let sum = 0;
  14.   for (let i = 1; i <= n; i++) {
  15.     sum = sum + i;
  16.   }
  18.   return sum;
  19. }

常见的时间复杂度实例分析

O.png

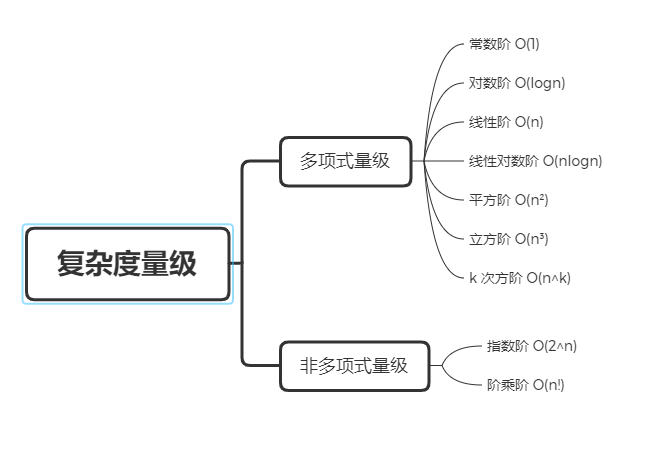
我们把时间复杂度为非多项式量级的算法问题较多 NP（Non-DeterministicPolynomial，非确定多项式）问题。

当数据规模 n 越来越大时，非多项式量级算法的执行时间会急剧增加，求解问题的执行时间会无限增长。 所以，非多项式时间复杂度的算法是一种非常低效的算法。

O(1)

O(1) 只是常量级时间复杂度的一种表示方法，并不指只执行一行代码。

  1. let i = 8;
  2. let j = 6;
  3. let sum = i + j;

只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂度我们都记作 O(1)。

一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万的代码，时间复杂度也为 O(1)。

O(logn)、O(nlogn)

对数时间复杂度非常常见。

  1. let i = 1;
  3. while (i <= n) {
  4.   i = i * 2;
  5. }

对于上面这个例子，只要我们能计算出这行代码被执行了多少次，就可以知道整段代码的时间复杂度。

变量 i 从 1 开始，每次循环都会乘以 2。当 i 大于 n 时，循环结束。

复杂度分析 - 图2 复杂度分析 - 图3 复杂度分析 - 图4 … 复杂度分析 - 图5 … 复杂度分析 - 图6 = n

我们可以通过 复杂度分析 - 图7 求解 x，即 复杂度分析 - 图8。所以时间复杂度为 复杂度分析 - 图9#card=math&code=O%28log2%5En%29);

现在再看这段代码：

  1. let i = 1;
  3. while (i <= n) {
  4.   i = i * 3;
  5. }

根据刚才的思路，很简单就可以看出，这段代码的时间复杂度为 复杂度分析 - 图10#card=math&code=O%28log3%5En%29)。

实际上，不管是以 2 为底，以 3 为底，还是以 10 为底，我们可以把所有对数阶时间复杂度都记为 复杂度分析 - 图11#card=math&code=O%28logn%29)。

采用大 O 标记复杂度的时候，可以忽略系数，即 O(Cf(n)) = O(f(n))。

我们介绍过计算时间复杂度的乘法法则，如果一段代码的时间复杂度是 复杂度分析 - 图12#card=math&code=O%28logn%29)，我们循环执行 n 遍，时间复杂度就是 复杂度分析 - 图13#card=math&code=O%28nlogn%29)。

O(m + n)、O(m * n)

代码的复杂度由两个数据的规模决定。

  1. function cal (m, n) {
  2.   let sum1 = 0;
  3.   for (let i = 1; i < m; i++) {
  4.     sum1 = sum1 + i;
  5.   }
  7.   let sum2 = 0;
  8.   for (let j = 1; j < n; j++) {
  9.     sum2 = sum2 + j;
  10.   }
  12.   return sum1 + sum2;
  13. }

由代码可以看出， m 和 n 是表示两个数据规模。

我们无法事先评估 m 和 n 谁的量级大，所以我们在表示复杂度的时候，就不能简单地利用加法法则，省略掉其中一个。

所以，上面代码的时间复杂度就是 O(m + n)。

针对上述情况，原来的加法法则就不正确了。 可以将加法法则改为 T1(m) + T2(n) = O(f(m) + g(n))。 乘法法则继续有效：T1(m) T2(n) = O(f(m) f(n))。

空间复杂度分析

时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的增长关系。

类比一下，空间复杂度全程就是渐进空间复杂度（asymptoic space complexity），表示算法的存储空间与数据规模之间的增长关系。

还是看下面例子（这段代码有点 low，主要是方便解释）。

  1. function print (n) {
  2.   let i = 0;
  3.   let a = [];
  5.   for (i; i < n; i++) {
  6.     a[i] = i * i;
  7.   }
  9.   for (i = n - 1; i >= 0; --i) {
  10.     console.log(a[i]);
  11.   }
  12. }

跟时间复杂度分析一样，我们可以看到，我们申请了一个空间存储变量 i，但是它是常量阶的，跟数据规模 n 没有关系，所以我们可以忽略。第 3 行申请了一个大小为 n 的数组，除此之外，剩下的代码没有占用更多空间，所以整段代码的空间复杂度就是 O(n)。

我们常见的空间复杂度就是 复杂度分析 - 图14%E3%80%81O(n)%E3%80%81O(n%5E2)#card=math&code=O%281%29%E3%80%81O%28n%29%E3%80%81O%28n%5E2%29)，像 复杂度分析 - 图15%E3%80%81O(nlogn)#card=math&code=O%28logn%29%E3%80%81O%28nlogn%29) 这样的对数阶复杂度平时都用不到。

而且，空间复杂度比时间复杂度分析要简单很多。

总结

复杂度也叫渐进复杂度，包括时间复杂度和空间复杂度，用来分析算法执行效率与数据规模之间的增长关系，可以粗略地表示，越高阶复杂度的算法，执行效率越低。常见的复杂度不多，从低阶到高阶有：复杂度分析 - 图16%E3%80%81O(logn)%E3%80%81O(n)%E3%80%81O(nlogn)%E3%80%81O(n%5E2)#card=math&code=O%281%29%E3%80%81O%28logn%29%E3%80%81O%28n%29%E3%80%81O%28nlogn%29%E3%80%81O%28n%5E2%29)。

复杂度分析并不难，关键在于多练。

技术拓展

项目性能测试和代码的复杂度分析是否冲突？

渐进式时间、空间复杂度分析和性能基准测试并不冲突，而是相辅相成的。一个低阶的时间复杂度程序极大的可能性会优于一个高阶的时间复杂度程序。所以在实际编程中，时刻关系理论时间，空间度模型是有助于产出效率高的程序的。

同时，因为渐进式时间，空间复杂度分析只是提供一个粗略的分析模型，因此也不会浪费太多时间。重点在于编程时，要具有这种复杂度分析的思维。